Enunciado
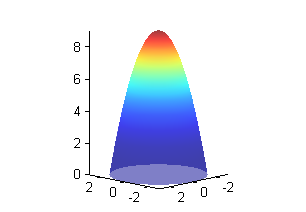
Si la temperatura en cada punto de la región del espacio donde se encuentra una lámina \(S\) es proporcional (\(k\)) al cuadrado de la distancia al origen de coordenadas, encuentra la temperatura media de la lámina \(S\) que toma la forma dada por \(z=9-x^2-y^2\) en \(z>0\). Encuentra también los puntos de la lámina donde se alcanza esa temperatura media.
Paso 1
Teniendo en cuenta cómo se realiza la integral de un campo escalar sobre una superficie dada en cartesianas, ver Integral de un campo escalar sobre una superficie, necesitamos determinar el elemento diferencial de superficie y la región de integración. Empecemos con el diferencial de superficie. Hállalo y pulsa en 'Ver'.
Ver
$$z'_x=-2x\ ,\ \ z'_y=-2y \ , \ \ dS=\sqrt{1+4(x^2+y^2)}\, dA$$
Paso 2
Busca ahora la región \(R_{xy}\) proyección de la superficie. Pulsa en 'Ver' cuando lo tengas.
Ver
Haciendo el corte de la superficie con el plano XY:
$$\left\{ \begin{array}{l} z=9-x^2-y^2 \\ z=0 \end{array}\right.\ \ \ \Rightarrow
\ \ \ x^2+y^2=9$$
sabemos que
$$R_{xy}=\{(x,y)/x^2+y^2\leq 9\}$$
que en polares es
$$R_{xy}=\{(r,\theta)/0\leq \theta \leq 2\pi ,\ r\leq 3\}$$
Paso 3
Calculamos ahora el área de la lámina \(S\). Vendrá dada por la integral
$$\int_0^{2\pi}\int_0^3 r \sqrt{1+4r}\, dr\, d\theta$$
$$\int_0^{2\pi}\int_0^3 \sqrt{1+4r^2}\, dr\, d\theta$$
$$\int_0^{2\pi}\int_0^3 r \sqrt{1+4r^2}\, d\theta \, dr$$
$$\int_0^{2\pi}\int_0^3 r \sqrt{1+4r^2}\, dr\, d\theta$$
Míralo bien, no has puesto bien el diferencial de superficie
Míralo bien, falta algo importante
Cuidado con el orden de los diferenciales
En efecto, esa integral doble da el área, luego
$$\mbox{área}(S)=\left.\frac{2\pi}{8}\frac{2}{3}(1+4r^2)^{3/2}\right]_0^3=\frac{\pi}{6}(37^{3/2}-1)$$
Paso 4
Calculemos ahora la integral de la función temperatura sobre la lámina. Según el enunciado, la temperatura en cada punto viene dada por
Ninguna de las dos propuestas es correcta
$$T(x,y,z)=k(x^2+y^2)$$
$$T(x,y,z)=k(x^2+y^2+z^2)$$
Míralo bien, sí hay una correcta
Míralo bien, falta algo
Sí, esta es la correcta. Por tanto la integral de la temperatura sobre la lámina es... Calcúlala y pulsa en 'Continuar'
La función temperatura sobre la lámina es
$$T(x,y,z)=k(x^2+y^2+(9-x^2-y^2)^2)=k(81-17(x^2+y^2)+(x^2+y^2)^2)$$
luego la integral en polares será
$$T_S=\int\!\! \int_S T(x,y,z) \, dS= k\int_0^{2\pi}\int_0^3 (81-17r^2+r^4)\, r \sqrt{1+4r^2} \, dr\, d\theta $$
La resolución de esta integral resulta trabajosa, por lo que se recomienda el uso de un programa de cálculo. Su valor es
$$T_S=k\frac{\pi}{14}(2146\sqrt{37}-193)$$
Esto quiere decir que $$T_m=\frac{T_S}{\mbox{área}(S)}=k\frac{3}{7}\frac{2146\sqrt{37}-193}{37\sqrt{37}-1}\approx 24.6 k$$
Paso 5
Sólo nos queda determinar el lugar geométrico de los puntos de la placa que están a temperatura media. Para localizarlos debemos igualar la función temperatura al valor medio. Resuélvelo y pulsa en 'Ver'.
Ver
$$T(x,y,z)=T_m \ \ \ \Rightarrow \ \ \ x^2+y^2+z^2=\frac{T_m}{k}$$
es decir, los puntos que están a temperatura media se sitúan en la esfera de radio \(\sqrt{T_m/k}\) y centro el origen, luego debemos intersecar esta esfera con la placa:
$$\left\{\begin{array}{l} x^2+y^2+z^2=T_m/k \\ x^2+y^2+z=9 \end{array}\right. \ \ \Rightarrow
\ \ z^2-z-(T_m/k-9)=0$$
Una de las raíces de esta ecuación es \(z\approx 4.5\) luego los puntos a temperatura media están situados en ese plano, ocupando la circunferencia \(x^2+y^2=4.5\).
Resumen
- Hallar el diferencial de superfice
- Encontrar la región proyección en el plano \(z=0\)
- Calcular el área de la placa
- Hallar la integral de la temperatura sobre la placa y su temperatura media
- Determinar los puntos de la placa donde la temperatura toma el valor medio