Paso 1
Obviamente en primer lugar debemos elegir los parámetros que se utilizarán para parametrizar \(S\): uno de los parámetros será la propia coordenada \(z\) y el otro será el ángulo \(\theta\) que da la variación angular respecto del eje OX con \(x\geq a\):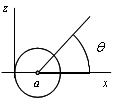
En estos parámetros las ecuaciones del semicilindro en \(y\) positivo completo (sin limitar la altura) son $$\begin{array}{c}\text{cilindro}\\ y>0\end{array}:(x-a)^2+y^2=a^2\ \ \rightarrow\ \ \left\{\begin{array}{l}x=a(1+\cos\theta)\\ y=a\sin\theta\\ z\end{array}\right.\theta\in [0,\pi]$$ ¿Cuál es la variación de \(z\)? Evidentemente vendrá dada por el corte con el semicono. Intenta buscarla y pulsa en 'Ver' cuando la tengas.
Ver
$$\begin{array}{c}\text{cono}\\ z>0\\ y>0\end{array}:z=\sqrt{2ax}\ \ \rightarrow \ \ z=\sqrt{2a^2(1+\cos\theta)}=\underbrace{2a\left|\cos\left(\frac{\theta}{2}\right)\right|}_{\text{¡OJO! Valor absoluto}(\sqrt{b^2}=|b|)}\overbrace{=}^{\frac{\theta}{2}\in\left[0,\frac{\pi}{2}\right]\ \Rightarrow\ \cos\frac{\theta}{2}>0}2a\cos\frac{\theta}{2}$$
Puesto que el área de la porción de cilindro para \(y\) positivo es la misma que para
\(y\) negativo, parametrizamos la primera:
$$S^*:\left\{\begin{array}{l}x=a(1+\cos\theta)\\ y=a\sin\theta\\ z\end{array}\right.\ \ ,\ \ \theta\in [0,\pi ],\ z\in\left[0,2a\left(\cos\frac{\theta}{2}\right)\right]$$