Enunciado
Encontrar el valor del área superficial de la
porción \(S\) del cilindro
\(x^2+y^2=2ax\)
comprendida entre el plano
\(z=0\)
y el semicono
\(z=\sqrt{x^2+y^2}\)
- Utilizando coodenadas cartesianas
- Utilizando ecuaciones paramétricas. (Ver ejercicio siguiente)
Resolución del primer apartado
Paso 1
Teniendo en cuenta cómo se calcula el área superficial en cartesianas, en primer lugar debemos analizar la superficie de la que debe calcularse una porción y determinar las simetrías. La porción \(S\) de la cual se pide el área es:
$$S=\{(x,y,z)/(x-a)^2+y^2\leq a^2,\, 0\leq z\leq \sqrt{x^2+y^2}\}$$
$$S=\{(x,y,z)/(x-a)^2+y^2\leq a^2,\, z=\sqrt{x^2+y^2}\}$$
$$S=\{(x,y,z)/(x-a)^2+y^2= a^2,\, z\geq \sqrt{x^2+y^2}\}$$
$$S=\{(x,y,z)/(x-a)^2+y^2= a^2,\, 0\leq z\leq \sqrt{x^2+y^2}\}$$
¡No! Esto no es una porción de superficie, sino que es una región de \(R^3\): el volumen contenido en el cilindro, sobre \(z=0\) y bajo el semicono \(z=\sqrt{x^2+y^2}\).
¡No! Esto es la porción del semicono que cae dentro del cilindro.
¡No! Esta sí es una superficie, pero es la porción de cilindro sobre el semicono, que será infinita.
En efecto, esa es la expresión de los puntos que forman la superficie de la que se calculará el área.
Paso 2
Debemos determinar sus simetrías. Analízalo y pulsa en 'Ver'.
Ver
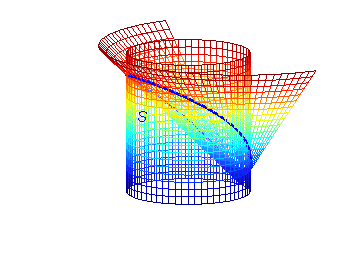
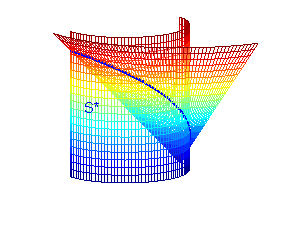
Puesto que todas las superficies son simétricas respecto al plano \(y=0\), la superficie
pedida es el doble de la correspondiente a \(y>0\):
$$S^*=\{(x,y,z)/0\leq x\leq 2a,y=\sqrt{2ax-x^2},0\leq z\leq \sqrt{x^2+y^2}\}$$


Paso 3
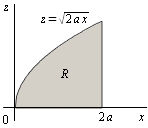
Para calcular el recinto de integración, debemos proyectar en el plano coordenado que nos parezca más adecuado. Puesto que los puntos de la superficie vienen dados por una función del tipo \(y=g(x,z)\), se proyectará en el plano XZ; debes conocer la curva intersección entre el semicono y el cilindro. Hállala y pulsa en 'Ver'.
Ver
$$\left. \begin{array}{l}x^2+y^2=2ax\\ z=\sqrt{x^2+y^2}\end{array}\right\}
\ \ \ \Rightarrow \ \ \ z=\sqrt{2ax}$$
con lo cual la región de integración es
$$R=\{(x,z)/0\leq x\leq 2a,0\leq z\leq \sqrt{2ax}\}$$
Paso 4
Una vez hallada la región de integración, para el planteamiento completo de la integral sólo falta el elemento diferencial de superficie. En este caso se calcula haciendo:
$$\begin{array}{l}z=f(x,y)=\sqrt{x^2+y^2} \\ f'_x=\frac{x}{\sqrt{x^2+y^2}},\ f'_y=\frac{y}{\sqrt{x^2+y^2}} \\ dS=\sqrt{1+f'_x^2+f'_y^2}\, dA=\sqrt{2}\,dA\end{array}$$
$$\begin{array}{l} y=g(x,z)=\sqrt{2ax-x^2} \\ g'_x=\frac{a-x}{\sqrt{2ax-x^2}},\ g'_z=0 \\ dS=\sqrt{1+g'_x^2+g'_z^2}\, dA=\frac{a}{\sqrt{2ax-x^2}}\, dA\end{array}$$
¡No! Has cogido el cono, no el cilindro. El diferencial de superficie que hace falta
es el del cilindro.
En efecto, ese es el diferencial de superficie del cilindro. El área superficial pedida es por tanto:
$$\mbox{Área}(S)=2\int\!\!\int_R \frac{a}{\sqrt{2ax-x^2}}\, dA\ \ \ , \ \ \mbox{con}\ \ \ R=
\{(x,z)/0\leq x\leq 2a,0\leq z\leq \sqrt{2ax}\}$$
Paso 5
Sólo falta calcular esa integral doble. Escribimos $$\mbox{Área}(S)=2a\int_a^{2a}{\int_0^\sqrt{2ax}{\frac{dz}{\sqrt{2ax-x^2}}}}\, dx$$ Sigue tú y pulsa en 'Ver' cuando la tengas.
Ver
$$\mbox{Área }S=2a\int_0^{2a}\frac{\sqrt{2a}\sqrt{x}}{\sqrt{2a-x}\sqrt{x}}\, dx=-4a\sqrt{2a}\int_0^{2a}{\frac{-dx}{2\sqrt{2a-x}}}=-4a\sqrt{2a}\left.\sqrt{2a-x}\right]_0^{2a}=8a^2$$
Resumen del primer apartado
- determinar la superficie de la que debe calcularse el área
- analizar sus simetrías
- determinar la región de integración
- calcular el diferencial de superficie
- calcular la integral