Definición: La superficie $S$ es suave si es la imagen de una función de clase ${C^1}$ definida en un dominio $D$

Veamos cómo se puede obtener el diferencial de superficie según venga definida la superficie $S$.

Superficie dada por $z=f(x,y)$

Tomamos la superficie $S$ imagen de $z=f(x,y)$, con $f(x,y)$ de clase $C^1$. El objetivo es encontrar una aproximación del área de $S$ que se proyecta sobre un rectángulo dado. Las dimensiones de ese rectángulo, que llamaremos $\Delta R$, son $\Delta x$ y $\Delta y$.

Puesto que la superficie más parecida a $S$ es su plano tangente, lo utilizaremos en esta aproximación. Tomaremos el plano tangente que pasa por un punto $P_0(x_0,y_0,f(x_0,y_0))$ y de él recortaremos la porción que se proyecta sobre el rectángulo $\Delta R$.

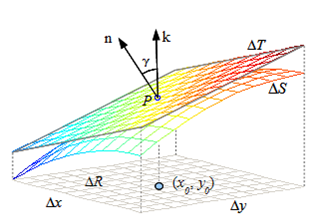
Considerando ${\bf n}$, el vector normal unitario a la superficie en el punto P, y $\gamma$, el ángulo entre los vectores ${\bf n}$ y ${\bf k}$, se cumple:

$$\Delta T = {1 \over {\left| {\cos \gamma } \right|}}\Delta R$$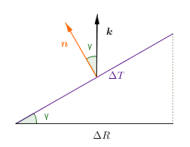

Como un vector normal a la superficie $S$ en $P$ es ${\bf N} = \left( { - f_x^'\left( {{x_o},{y_o}} \right), - f_y^'\left( {{x_o},{y_o}} \right),1} \right)$, podemos escribir

$$\left| {\cos \gamma } \right| = \left| {\bf n} \cdot {\bf k} \right| = {1 \over {\left| {\bf N} \right|}}$$

luego

$$\Delta T=|{\bf N}|\,\,\Delta R\, \,=\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}\,\,\Delta x\,\, \Delta y$$

Cuando las dimensiones de $\Delta R$ tiendan a cero, $\Delta T$ tenderá al llamado elemento diferencial de superficie: \begin{equation} \label{t5e1}dS=\sqrt{f'_x(x,y)^2+f'_y(x,y)^2+1}\, dx\, dy \end{equation}

Superficie dada por $F(x,y,z)=0$

Si la superficie viene expresada por una función implícita, $F(x,y,z)=0$, con $F$ de clase $C^1$ siendo $F'_z\neq 0$, el vector normal en cada punto es $${\bf N}=\left( \frac{F'_x}{F'_z},\frac{F'_y}{F'_z},1\right)$$

El elemento diferencial de superficie es: $$dS=\frac{\sqrt{{F'_x}^2+{F'_y}^2+{F'_z}^2}}{|F'_z|}\, dx\, dy$$

Superficie dada en paramétricas

Si la superficie viene expresada por la imagen de unas ecuaciones paramétricas: $${\bf r}(u,v):\left\{\begin{array}{l} x=x(u,v) \\ y=y(u,v) \\ z=z(u,v) \end{array}\right.\ \ \ (u,v)\in R$$ los dos vectores tangentes a la superficie por el punto $(x(u,v),y(u,v),z(u,v))$ son $${\bf r_u}=(x'_u(u,v),y'_u(u,v),z'_u(u,v)) \ \ \ \mbox{y}\ \ \ {\bf r_v}=(x'_v(u,v),y'_v(u,v),z'_v(u,v))$$ y el vector normal es $${\bf N}={\bf r_u}\times {\bf r_v}$$

 

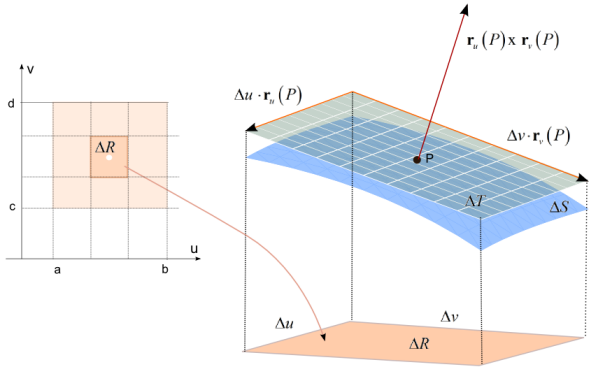
El área de la porción de plano tangente que se proyecta en $\Delta R $ es $$\Delta T = \left| {{{\bf r_u}}\left( P \right)\times{{\bf r_v}}\left( P \right)} \right|\Delta u\,\Delta v$$

Cuando $\Delta u \to 0$ y $\Delta v \to 0$, entonces $\Delta T \to dS$, por lo que la expresión para el diferencial de superficie es $$dS=|{\bf r_u}\times {\bf r_v}|\, du\, dv$$