Una función $f(x,y,z)$ es integrable en un conjunto $V \subset {R^3}$ si lo es en una caja que contenga a $V$.

La definición, las condiciones de existencia y las propiedades de la integral triple sobre cajas recogidas en el apartado anterior, son aplicables a la integral triple sobre dominios regulares sin más que sustituir $H$ por $V$.

Existen tres tipos de dominios regulares en $R{^3}$ : x-simple, y-simple, z-simple. Un dominio puede ser de los tres tipos simultáneamente.

Se describe el proceso de cálculo para el caso de dominio z-simple, los restantes casos se deducen de éste sin dificultad.

Definición (Dominio regular z-simple).- Un conjunto $H$ del espacio es z-simple si se puede escribir como, $$H = \{ (x,y,z)/\;(x,y) \in {R_{xy}},\,{\kern 1pt} \,\,{\psi _1}(x,y) \le z \le {\psi _2}(x,y)\} $$ siendo además $R_{xy}$ un dominio regular del plano $XY$.

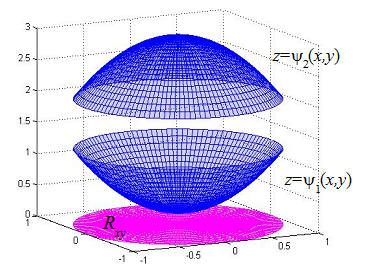
Definición (Integrales iteradas sobre un dominio regular z-simple).- Si un conjunto $H$ del espacio es z-simple y la función $f(x,y,z)$ es integrable en $H$, entonces $$\int \int \int_H \,f(x,y,z){\kern 1pt} dV = \int \int_{{R_{xy}}} \left[ {\int_{\,{\psi _1}(x,y)}^{\,{\psi _2}(x,y)} f(x,y,z){\kern 1pt} dz} \right]{\kern 1pt} dA$$ Si además, $${R_{xy}} = \{ (x,y)/a \le x \le b,{\kern 1pt} \,\,{\phi _1}(x) \le y \le {\phi _2}(x)\} $$ la integral anterior es $$\int \int \int_H \,f(x,y,z){\kern 1pt} dV = \int_{\,a}^{\,b} \int_{\,{\phi _1}(x)}^{\,{\phi _2}(x)} \int_{\,{\psi _1}(x,y)}^{\,{\psi _2}(x,y)} f(x,y,z){\kern 1pt} dz{\kern 1pt} dy{\kern 1pt} dx$$

Según sea la forma de $H$ y de $f$, puede ser recomendable utilizar otro orden de integración.