El teorema sobre cambio de variable en integrales triples se obtiene del visto para integrales dobles con las modificaciones obvias resultantes de añadir una variable más.
El jacobiano del cambio de variables $$x = x(u,v,w)\;\;,\;\;y = y(u,v,w)\;\;,\;\;z = z(u,v,w)$$ es el determinante $$J = {{\partial (x,y,z)} \over {\partial (u,v,w)}} = \left| {\matrix{ {{{x'}_u}} & {{{x'}_v}} & {{{x'}_w}} \cr {{{y'}_u}} & {{{y'}_v}} & {{{y'}_w}} \cr {{{z'}_u}} & {{{z'}_v}} & {{{z'}_w}} \cr } } \right|$$

Cambio a coordenadas cilíndricas

Para el cambio de variables $$x = r\cos \theta ,\,\,\,\,\,\,y = r\, {\mathop{\rm sen}\nolimits} \theta ,\,\,\,\,\,\,z = z$$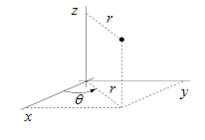

El jacobiano es $$J = {{\partial (x,y,z)} \over {\partial (r,\theta ,z)}} = \left| {\matrix{ {\cos \theta } & { - r{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta } & 0 \cr {{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta } & {r\cos \theta } & 0 \cr 0 & 0 & 1 \cr } } \right| = r$$

Y el elemento diferencial de volumen, $dV = dx{\kern 1pt} dy{\kern 1pt} dz$, en cilíndricas es $dV = r{\kern 1pt} dr{\kern 1pt} d\theta {\kern 1pt} dz$:

puesto que $r$ es no negativo.

Relación entre coordenadas cilíndricas y cartesianas

Las coordenadas cilíndricas se obtienen utilizando coordenadas polares en uno de los planos coordenados, de forma que son las apropiadas para describir conjuntos del espacio, como el interior de un cilindro, que tienen un eje de simetría. Si ese eje de simetría es el eje $OZ$, las coordenadas cartesianas se escribirán del siguiente modo en función de las cilíndricas: $$\left\{ {\matrix{ {x = r\cos \theta } \cr {y = r{\kern 1pt} sen{\kern 1pt} {\kern 1pt} \theta } \cr {z = z} \cr } } \right.$$

Las superficies de ecuación más sencilla en coordenadas cilíndricas son:

• $r = a$: es el cilindro de eje $OZ$ y radio $a$;
• $\theta = b$ es el semiplano que contiene al eje $OZ$ y forma ángulo $b$ con el plano $XZ$, ($x > 0$);
• $z = c$: es un plano perpendicular al eje $0Z$.

Cambio a coordenadas esféricas

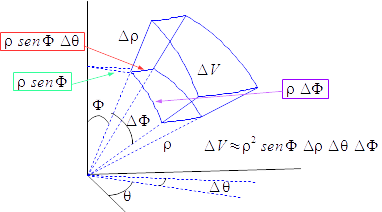
Para el cambio de variables $$x = \rho {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi \cos \theta \;\;,\;\;y = \rho {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta \;\;,\;\;z = \rho \cos \phi $$ el jacobiano es $$J = {{\partial (x,y,z)} \over {\partial (\rho ,\theta ,\phi )}} = {\rho ^2}{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi $$
El elemento diferencial de volumen $dV = dx{\kern 1pt} dy{\kern 1pt} dz$ en esféricas es $$dV = {\rho ^2}|{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi |{\kern 1pt} d\rho {\kern 1pt} d\theta {\kern 1pt} d\phi $$

Relación entre coordenadas esféricas y cartesianas

Las coordenadas esféricas son útiles en sólidos acotados por esferas, planos que pasan por el eje $OZ$ y conos con ese eje. Es decir, aquellos volúmenes en los que existe un centro de simetría.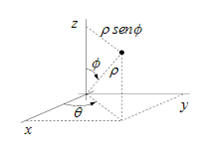

Las fórmulas del cambio son: $$\left\{ {\matrix{ {x = \rho {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi \cos \theta } \cr {y = \rho {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \phi {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta } \cr {z = \rho \cos \phi }  \cr } } \right.$$ Las variables del sistema representan las siguientes magnitudes geométricas:

• $\rho $ : distancia del punto al origen de coordenadas,
• $\theta $: ángulo de variación respecto del eje $OX$ positivo, se toma entre 0 y $2\pi $ ;
• $\phi $: ángulo de variación respecto del eje $0Z$ positivo, se toma entre 0 y $\pi$.

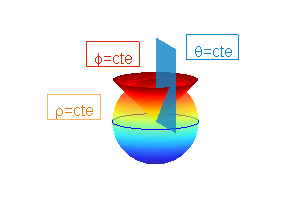
Las superficies de ecuación más sencilla en coordenadas esféricas son:

• $\rho = a$: es la esfera de centro el origen y radio $a$;
• $\theta = b$ : es el semiplano que contiene al eje $0Z$ y forma ángulo $b$ con el plano $XZ$ , ( $x > 0$);
• $\phi = c$: es un semicono de eje $0Z$.