Enunciado
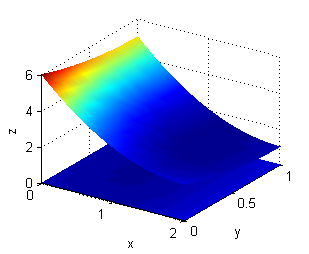
Tomemos de nuevo el sólido $S$ que ocupa la región del primer octante limitada inferiormente por el rectángulo $R=[0,a]\times[0,b]$ del plano $XY$ y superiormente por la superficie $z=c+(x-a)^2+(y-b)^2$ (con $c>0$) considerando el caso particular $a=2$, $b=1$ y $c=1$. Toma la función temperatura $T$ que en cada punto vale el cuadrado de la distancia a un punto $(x_0,y_0,z_0)$ dentro de la caja $H=[0,a]\times[0,b]\times[0,c]$.
- Con el ordenador, encuentra la expresión de la temperatura media del sólido.
- Dibuja varias secciones de la caja $H$ coloreadas según la función que asigna a cada punto
$(x_0,y_0,z_0)$ de la caja el valor de la temperatura media.
- Localiza el punto $(x_0,y_0,z_0)$ preciso para que esa temperatura media sea la mayor posible.
- Localiza el punto $(x_0,y_0,z_0)$ preciso para que esa temperatura media sea la menor posible
- Dibuja dos figuras, una con las tapas superior e inferior del sólido coloreadas según la temperatura que produce un valor medio máximo y otra con esas tapas coloreadas con la temperatura cuyo valor medio es mínimo.
Resolución del primer apartado
Escribe las líneas necesarias para
- asignar los valores a $a$, $b$ y $c$ y declarar simbólicas a $x$, $y$, $z$, $x0$, $y0$ y $z0$;
- calcular el volumen del sólido
- calcular la integral de la función temperatura
- hallar la temperatura media
Ver
Con
a=2;b=1;c=1; syms x y z x0 y0 z0 v= double(int(int(int(1,z,0,c+(x-a)^2+(y-b)^2),y,0,b),x,0,a));% volumen t0= int(int(int((x-x0)^2+(y-y0)^2+(z-z0)^2,z,0,c+(x-a)^2+(y-b)^2),y,0,b),x,0,a);%integral de la temperatura tm0=t0/v % expresión de la temperatura mediaencontraremos la expresión $tm0$ del valor medio de $T(x,y,z)=(x-x0)^2+(y-y0)^2+(z-z0)^2$ en el sólido $S$:
tm0 = x0^2 - (3*x0)/2 + y0^2 - (15*y0)/16 + z0^2 - (97*z0)/30 + 8719/1680Observa que para $(x0,y0,z0)=(0,0,0)$, este valor es el obtenido en el primer ejercicio sobre este sólido.
Resolución del segundo apartado
Para dibujar unas secciones de la caja $H=[0,2]\times[0,1]\times[0,1]$ coloreadas según la función $tm0$, añadimos a las líneas anteriores las necesarias para $\ldots$ (pulsa en continuar cuando hayas escrito cada una)- genera una malla de puntos en la caja $H$, llámala $[X,Y,Z]$
[X,Y,Z]=meshgrid(0:.05:2,0:.1:1,0:.1:1);
- utiliza la expresión simbólica $tm0$ para generar una matriz, $TM$, con los valores de $tm0$ sobre los puntos de la malla $[X,Y,Z]$ (recuerda el comando subs)
TM=subs(tm0,{x0 y0 z0},{X,Y,Z});
- genera un vector, llámalo $seccx$, con los valores del eje $0X$ por lo que quieras pintar secciones $x$ constante; igualmente genera $seccy$ y $seccz$ para los ejes $0Y$ y $0Z$, respectivamente
por ejemplo, para que dibuje las secciones $x=.5$, $x=1$, $x=1.5$, $x=2$, $y=.2$, $y=.4$, $y=.6$, $y=.8$ y $z=.5$, pondremos
seccx = .5:.5:2; seccy = .2:.2:.8; seccz = .5;
- por último, utiliza el comando slice para dibujar esas secciones coloreadas
slice(X,Y,Z,TM,seccx,seccy,seccy)Ejecutando estas líneas a continuación de las del primer apartado, obtendremos la siguiente figura
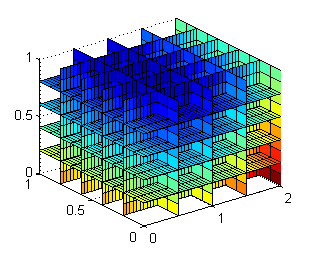
Podemos girarla para ver la cara $x=0$, por ejemplo con
view([30,34])veremos
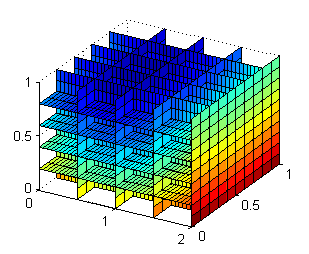
Resolución del tercer apartado
Debemos hallar el máximo de la función $$tm_0 = x_0^2 - \frac{3}{2}x_0 + y_0^2 - \frac{15}{16}y_0 + z_0^2 - \frac{97}{30}z_0 + \frac{8719}{1680}$$ Sabemos que ese máximo se alcanza para algún $(x_0,y_0,z_0)$ en $H$ porque $tm_0$ es una función continua y $H$ es un conjunto cerrado y acotado. Así que lo más apropiado aquí es
Hallar los puntos críticos de $tm_0$.
Utilizar el método de los multiplicadores de Lagrange.
Ninguna de las propuestas es la adecuada.
Completar cuadrados en la expresión de $tm_0$.
Se podría, pero no es lo más adecuado aquí.
¿Cuál es la condición?
Sí hay una propuesta adecuada.
En efecto, podemos completar cuadrados en $tm_0$, para escribirlo como suma de tres cuadrados y una constante; inténtalo y pulsa en 'Continuar'.
Completando cuadrados, tendremos
$$tm_0=\left(x_0-\frac{3}{4}\right)^2+\left(y_0-\frac{15}{32}\right)^2+\left(z_0-\frac{97}{60}\right)^2+\frac{8719}{1680}-\frac{9}{16}-\frac{15^2}{32^2}-\frac{97^2}{60^2}$$
lo que significa que $tm_0$ será máximo cuando los números
$$\left|x_0-\frac{3}{4}\right| \hspace{.3cm},\hspace{.4cm}
\left|y_0-\frac{15}{32}\right| \hspace{.3cm},\hspace{.4cm}
\left|z_0-\frac{97}{60}\right|$$
sean máximos, teniendo en cuenta que
$$0\leq x_0\leq 2 \hspace{.3cm},\hspace{.4cm} 0\leq y_0\leq 1\hspace{.3cm},\hspace{.4cm}
0\leq z_0\leq 1$$
Localiza los valores de $x_0$, $y_0$ y $z_0$ que hacen máximos esos valores absolutos y pulsa en 'Ver'.
Ver
puesto que $\frac{3}{4}<1$, $\frac{15}{32}<1$ y $\frac{97}{60}>1$, los valores de $x_0$, $y_0$ y $z_0$ que hacen máximos esos valores absolutos y por tanto la función $tm_0$ son
$$x_0=2 \hspace{.3cm},\hspace{.4cm} y_0=1 \hspace{.3cm},\hspace{.4cm} z_0=0$$
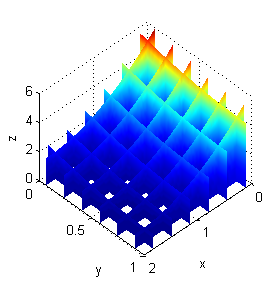
A continuación puedes ver varias secciones del sólido completo coloreadas segun la función temperatura
$$T_0(x,y,z)=(x-2)^2+(y-1)^2+z^2$$

Resolución del cuarto apartado
Aprovechamos la expresión de $tm_0$ conseguida antes: $$tm_0=\left(x_0-\frac{3}{4}\right)^2+\left(y_0-\frac{15}{32}\right)^2+\left(z_0-\frac{97}{60}\right)^2+\frac{8719}{1680}-\frac{9}{16}-\frac{15^2}{32^2}-\frac{97^2}{60^2}$$ para hallar los valores de $x_0$, $y_0$ y $z_0$ que hacen mínimo $tm_0$; puesto que cero es lo menos que puede valer cada cuadrado de esa expresión, el mínimo se alcanza para
$$x_0=\frac{3}{4} \hspace{.3cm},\hspace{.4cm} y_0=\frac{15}{32} \hspace{.3cm},\hspace{.4cm} z_0=\frac{97}{60}$$
la propuesta no es correcta
No es correcto, fíjate que $\frac{97}{60}>1$.
En efecto, el valor de $z_0$ no es correcto, pues $\frac{97}{60}>1$. El valor de $z_0$ que, sin salirnos de la caja $H$, hace mínimo $tm_0$ es $z_0=1$. Así que el punto es el de coordenadas
$$x_0=\frac{3}{4} \hspace{.3cm},\hspace{.4cm} y_0=\frac{15}{32} \hspace{.3cm},\hspace{.4cm} z_0=1$$
Puedes observar en las secciones que dibujaste en el segundo apartado cómo la zona que rodea este punto es la coloreada con azul más oscuro. A continuación puedes ver varias secciones del sólido completo coloreadas segun la función temperatura
$$T_0(x,y,z)=(x-\frac{3}{4})^2+(y-\frac{15}{32})^2+(z-1)^2$$
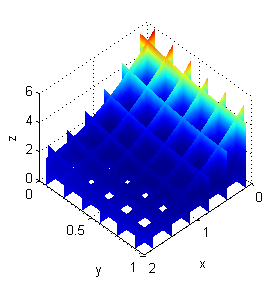

Resolución del quinto apartado
Para hacer esas figuras, podemos generar una función. Sus variables de entrada serán $x_0$, $y_0$ y $z_0$ y generará una figura con las caras superior e inferior del sólido coloreadas según la función $$T_0(x,y,z)=(x-x_0)^2+(y-y_0)^2+(z-z_0)^2$$
function tempmediasolg(x0,y0,z0)
a=2;b=1;c=1;
x=linspace(0,a,20);
y=linspace(0,b,20);
[X,Y]=meshgrid(x,y); % malla de puntos en R
Z=c+(X-a).^2+(Y-b).^2; % valores de la z superior
T=(X-x0).^2+(Y-y0).^2+(Z-z0).^2; % valores de la temperatura en la cara superior
surf(X,Y,Z,T) % tapa superior coloreada según la temperatura
hold on
T=(X-x0).^2+(Y-y0).^2+z0^2; % valores de la temperatura en la cara inferior
surf(X,Y,zeros(size(X)),T)
hold off
shading interp
view([34,32])
xlabel('x');ylabel('y');zlabel('z'); % etiquetas para los ejes
end
Ejecutando
tempmediasolg(2,1,0)obtendremos la siguiente figura con las caras superior e inferior del sólido coloreadas según la temperatura $$T_0(x,y,z)=(x-2)^2+(y-1)^2+z^2$$ que como sabemos es, de todas las de esa forma, la que hace máximo el valor de la temperatura media:
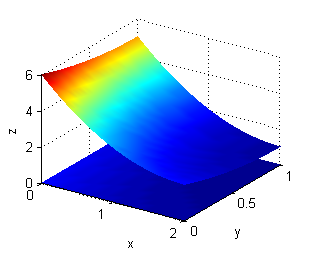
Ejecutando
tempmediasolg(3/4,15/32,1)obtendremos la siguiente figura con las caras superior e inferior del sólido coloreadas según la temperatura $$T_0(x,y,z)=(x-\frac{3}{4})^2+(y-\frac{15}{32})^2+(z-1)^2$$ que es, de todas las de esa forma, la correspondiente al mínimo valor de la temperatura media: