Enunciado
Un sólido $S$ ocupa la región del primer octante del espacio limitada inferiormente por el rectángulo $R=[0,2]\times[0,1]$ del plano $XY$ y superiormente por la superficie $z=1+(x-2)^2+(y-1)^2$
- Halla el volumen de $S$.
- Encuentra los puntos de $S$ que están a temperatura media si ésta en cada punto es el cuadrado de la distancia al origen de coordenadas. Utiliza el ordenador para calcular las integrales.
- Dibuja la superfice $z=1+(x-2)^2+(y-1)^2$ en $R=[0,2]\times[0,1]$ coloreada según la función temperatura y el conjunto de puntos que están a temperatura media.
- Repite los dos primeros apartados tomando el rectángulo $R=[0,a]\times[0,b]$, sobre él la superficie $z=c+(x-a)^2+(y-b)^2$ como superficie limitante ($c>0$) y la misma función temperatura.
Resolución del primer apartado
Paso 1
Saber qué integral debe hacerse: qué se integra y dónde se integra. Calcular el volumen de un sólido puede hacerse con una integral doble o con una integral triple. En este caso, es bastante sencillo plantearlo como una integral doble: $$\mbox{Volumen}=\int\!\!\int_R z(x,y)\, dA$$ si $z=z(x,y)$ es la superficie que limita al sólido superiormente y $R$ es su proyección en el plano $XY$, da el valor del volumen del sólido limitado entre el plano $XY$ y $z=z(x,y)$.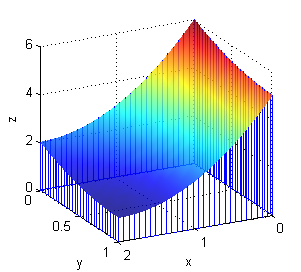
Escribe la integral anterior como dos iteradas y pulsa en 'Ver'.
Ver
Podemos poner
$$\mbox{Volumen}(S)=\int_0^2\int_0^1 (1+(x-2)^2+(y-1)^2)\, dy\, dx$$
o
$$\mbox{Volumen}(S)=\int_0^1\int_0^2 (1+(x-2)^2+(y-1)^2)\, dx\, dy$$
En este caso no hay ventajas en tomar una u otra a la hora de calcular la integral. Aquí lo resolveremos siguiendo la primera opción.
Paso 2
Calcular las integrales iteradas. Hazlas tú y pulsa en 'Ver'.
Ver
Una vez que se calcula la más interior, resulta
$$\mbox{Volumen}(S)=\int_0^2\left ((x-2)^2+\frac{4}{3} \right )\, dx$$
y haciendo la segunda,
$$\mbox{Volumen}(S)=\frac{16}{3} $$
Resolución del segundo apartado
Recordando las interpretaciones de la integral triple, sabemos que la temperatura media se calcula dividiendo la integral de la temperatura entre el volumen del sólido.Paso 1
Encontrar la integral de la función temperatura en el sólido. Ahora sí es imprescindible hacer una integral triple. La región de integración es $$S=\{(x,y,z) / \, 0\leq x\leq 2 ,\ 0\leq y\leq 1, \ 0\leq z\leq 1+(x-2)^2+(y-1)^2\}$$ y la función temperatura que debemos integrar es
$T(x,y,z)=x+y+z$
$T(x,y,z)=|x|+|y|+|z|$
$T(x,y,z)=x^2+y^2+z^2$
No, eso no es el cuadrado de la distancia entre $(x,y,z)$ y el origen.
No, eso no es el cuadrado de la distancia entre $(x,y,z)$ y el origen.
En efecto, esa es la función temperatura.
En la siguiente figura puedes ver varias secciones del sólido coloreadas según esa función temperatura.
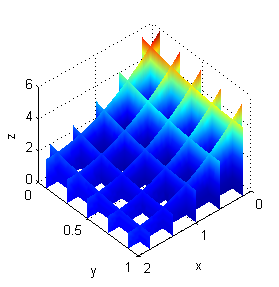
Por tanto debe calcularse $$I=\int_0^2\int_0^1 \int_0^{1+(x-2)^2+(y-1)^2} (x^2+y^2+z^2)\, dz\, dy\, dx$$ Escribe las líneas de código necesarias para evaluar esa integral con el paquete simbólico y pulsa en 'Continuar'.

Por tanto debe calcularse $$I=\int_0^2\int_0^1 \int_0^{1+(x-2)^2+(y-1)^2} (x^2+y^2+z^2)\, dz\, dy\, dx$$ Escribe las líneas de código necesarias para evaluar esa integral con el paquete simbólico y pulsa en 'Continuar'.
Con
syms x y z I= int(int(int(x^2+y^2+z^2,z,0,1+(x-2)^2+(y-1)^2),y,0,1),x,0,2)obtendremos
I =8719/315
Paso 2
Calcular la temperatura media. Este es un paso fácil, pues ya tenemos los dos datos necesarios: $$T_m=\frac{I}{\mbox{Volumen}(S)}=\frac{8719}{1680}\approx 5.1899$$Paso 3
Determinar el lugar geométrico de los puntos que están a esa temperatura media. Puesto que en cada punto la temperatura es $T(x,y,z)=x^2+y^2+z^2$, los puntos a temperatura $T_m=\frac{8719}{1680}$ son $$x^2+y^2+z^2=\frac{8719}{1680}$$ es decir los puntos de $S$ que están en la esfera de centro el origen y radio $\sqrt{\frac{8719}{1680}}=2.2781$.Resolución del tercer apartado
Para dibujar la 'tapa superior' del sólido coloreada según su temperatura y el conjunto de puntos donde la temperatura es media, podemos hacer:- generar la malla en el rectángulo $R$
[X,Y]=meshgrid(0:.1:2,0:.05:1);
- definir una matriz con los valores de la superficie sobre la malla
Z=1+(X-2).^2+(Y-1).^2;
- definir una matriz con los valores de la temperatura en la superficie
T=X.^2+Y.^2+Z.^2;
- dibular la superficie, debemos incluir en el cuarto argumento la matriz $T$ para que coloree la superficie según sus valores
surf(X,Y,Z,T) % 'tapa' del sólido shading interp
- poner nombres a los ejes coordenados
xlabel('x');ylabel('y');zlabel('z'); - fijar el rango para los ejes
axis([0 2 0 1 0 6])
- una vez ejecutado, buscar una orientación apropiada y fijarla
view([153,22])
- darle un cierto grado de transparencia para poder visualizar la otra superficie
alpha(.6)
- mantener abierta la figura para dibujar en la misma ventana otra superficie
hold on
- definir tm con el valor de la temperatura media
tm=8719/1680;
- dibujar la superficie $z=\sqrt{tm-x^2-y^2}$, incluyendo como cuarto argumento una matriz de las mismas dimensiones que $X$ 0 $Y$ que repita en todas sus componentes el valor de la temperatura media
surf(X,Y,sqrt(tm-X.^2-Y.^2),tm*ones(size(X))) shading interp
- 'cerrar' la figura
hold off
[X,Y]=meshgrid(0:.1:2,0:.05:1);
Z=1+(X-2).^2+(Y-1).^2;
T=X.^2+Y.^2+Z.^2;
surf(X,Y,Z,T) % 'tapa' del sólido
shading interp
xlabel('x');ylabel('y');zlabel('z');
axis([0 2 0 1 0 6])
view([153,22])
alpha(.6)
hold on
tm=8719/1680;
surf(X,Y,sqrt(tm-X.^2-Y.^2),tm*ones(size(X)))
shading interp
hold off
y ésta es la figura que obtendremos: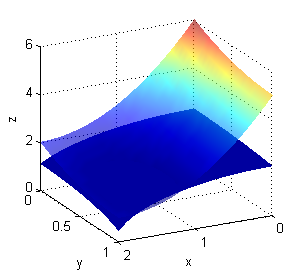
Resolución del cuarto apartado
Paso 1
Calcular el volumen. Podemos seguir el mismo procedimiento que en el primer apartado, cuidando de actualizar los valores de los límites de integración y la constante $c$ que aparece ahora en la función. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
$$\mbox{Volumen}(S)=\int_0^a \int_0^b (c+(x-a)^2+(y-b)^2)\, dy\, dx$$
Tras hacer la primera integral, tendremos
$$\mbox{Volumen}(S)=\int_0^a \left(bc+b(x-a)^2+\frac{1}{3}b^3\right)\, dx$$
y tras hacer esta integral simple resulta
$$\mbox{Volumen}(S)=abc+\frac{1}{3}ab(a^2+b^2)$$
Paso 2
Hallar la integral de la temperatura: $$I=\int_0^a\int_0^b \int_0^{c+(x-a)^2+(y-b)^2} (x^2+y^2+z^2)\, dz\, dy\, dx$$ Para este cálculo utilizamos de nuevo el ordenador. Escribe las líneas necesarias para hallar esta integral con el paquete simbólico y pulsa en 'Ver'.
Ver
Con
syms x y z a b c I= int(int(int(x^2+y^2+z^2,z,0,c+(x-a)^2+(y-b)^2),y,0,b),x,0,a)obtendremos que $$I=\frac{1}{21} ab+\frac{1}{5}\left(b+\frac{1}{3}b^3\right)a^5+\frac{1}{3}\left(\frac{2}{3}b^3+\frac{1}{5}b^5\right)a^3+\frac{1}{5}ab^5+\frac{1}{7}ab^7$$