Sumas de Riemann para conjunto de datos (caso 1)

Enunciado

Este ejercicio trata sobre el cálculo de las sumas de Riemann en el supuesto de que no se conozca la expresión de la función de dos variables cuyas sumas deben evaluarse, sino únicamente una muestra de valores sobre una malla de puntos de un rectángulo. Nos ocuparemos de dos casos: que los puntos estén igualmente espaciados o que no lo estén; el primer supuesto es con el que se trabaja en este ejercicio, dejando el segundo para otro enunciado.

CASO 1: Los puntos de la malla están igualmente espaciados en cada eje; por ejemplo, el conjunto de puntos de la malla tiene de abscisas $[0,\, .2 ,\, .4 ,\, .6,\, .8 ,\, 1]$ y de ordenadas $[1,\, 1.3,\, 1.6,\, 1.9,\, 2.2,\, 2.5,\, 2.8,\, 3.1]$ (figura de la izquierda)

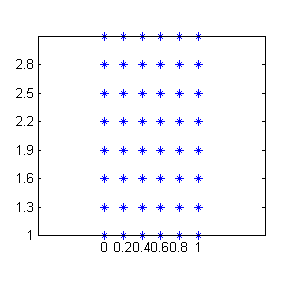
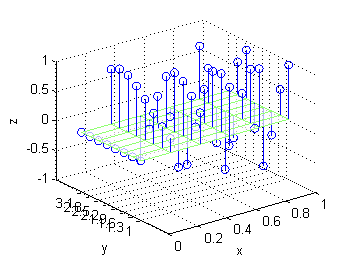
Lo que conocemos de la función son los valores (ver figura de la derecha) en puntos sobre la malla formada por estas abscisas y estas ordenadas; por tanto en este ejemplo, estos valores se agruparán en una matriz de dimensión $6\times 8$.

Escribe una función, llámala sumasRdatos1, que tenga como variable de entrada el vector de abscisas, el vector de ordenadas de los puntos de la malla y la matriz de datos y que tenga como salida la suma de Riemann correspondiente.
Pruébala con los puntos indicados antes y la matriz de datos que se generaría evaluando la función $f(x,y)=\mbox{sen}(xy^2+x^2)$ sobre esta red de puntos.
Además de por comodidad, hemos generado así la matriz de datos para poder tener una idea de la proximidad de la suma de Riemann obtenida al valor que se obtiene integrando, con el paquete simbólico, la función $f$ sobre el rectángulo $R=[0 ,1.2]\times[1 ,3.4]$. Analiza esa proximidad.

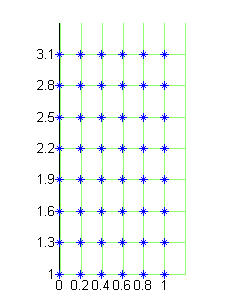
CASO 2: Los puntos de la malla no están igualmente espaciados en uno o en los dos ejes: ver siguiente ejercicio.

Resolución del primer apartado del CASO 1

Como sabemos, hemos de empezar la función con la declaración

function s=sumasRdatos1(x,y,D)

donde $x$ es la variable que guardará el vector de abscisas, $y$ es para el vector de ordenadas y $D$ para la matriz de datos. A continuación hemos de tener claro qué datos necesita esta función sumasRdatos1 para calcular la suma de Riemann. Piénsalo y pulsa en 'Ver'.

Ver

En efecto, puesto que los valores de la función ya se van a dar como una variable de entrada, lo único que debe calcular sumasRdatos1 son los incrementos en cada eje. Piensa qué línea de código puedes incluir para que se calculen estos incrementos y formen un vector llamado inc; pulsa en 'Continuar' cuando lo tengas.

Podemos poner

inc=abs([x(2)-x(1),y(2)-y(1)]); % vector con los incrementos en cada eje

Piensa ahora cómo mandarle calcular la suma de Riemann.

En efecto, basta con escribir

s=prod(inc)*sum(D(:)); % suma de Riemann

y sólo queda cerrar la función. Toda la función resulta

function s=sumasRdatos1(x,y,D)
inc=abs([x(2)-x(1),y(2)-y(1)]); % vector con los incrementos en cada eje
s=prod(inc)*sum(D(:)); % suma de Riemann
end

Siempre es conveniente escribir unas líneas de comentario tras la línea de declaración de la función. Eso dejamos que lo termines tú. No olvides tampoco que la función debe ir en un fichero llamado sumasRdatos1.m

Resolución del segundo apartado del CASO 1

Para probar sumasRdatos1(x,y,D) podemos introducir los vectores x e y y la matriz D del enunciado. Lo haremos con

x=0:.2: 1; y=1:.3:3.1;
D=sin(x.*y.^2+x.^2);

no se hace así

No es correcto, se te ha olvidado generar la malla.

En efecto, la otra propuesta no es correcta, pues hemos de evaluar $f(x,y)=\mbox{sen}(xy^2+x^2)$ no sobre la x y la y, sino sobre los puntos de una malla. Escríbelo correctamente y pulsa en 'Continuar'.

Pondremos

x=0:.2: 1; y=1:.3:3.1;
[X,Y]=meshgrid(x,y);
D=sin(X.*Y.^2+X.^2);

Ahora ya podemos ejecutar la función sumasRdatos1(x,y,D):

s=sumasRdatos1(x,y,D);

Nos devolverá $s=0.7366$.

Resolución del tercer apartado del CASO 1

Hemos de calcular la integral de la función $f(x,y)=\mbox{sen}(xy^2+x^2)$ sobre el rectángulo $R=[0 ,1.2]\times[1 ,3.4]$ utilizando el comando int. Hazlo tú y pulsa en 'Ver' cuando lo tengas.

Ver

Escribimos

syms xs ys
double(int(int(sin(xs*ys^2+xs^2),xs,0,1.2),ys,1,3.4))

que nos devuelve el valor $0.6606$.

Índice de tema