Índice de tema

 

Enunciado

Encuentra el valor de la temperatura media de una placa que ocupa la región del plano $$D=\{(x,y)/\,|x|+|y|\leq 1\}$$ sabiendo que la temperatura en cada punto $(x,y)$ es $$T(x,y)=e^{x+y}$$ Dibuja previamente la región $D$.

Paso 1

En primer lugar hemos de dibujar la región $D$ ocupada por la placa. Según el signo de $x$ y de $y$ en los distintos cuadrantes del plano, la expresión $|x|+|y|= 1$ es
  • primer cuadrante ($x>0$, $y>0$): $y=1-x$
  • segundo cuadrante ($x<0$, $y>0$): $y=1+x$
  • tercer cuadrante ($x<0$, $y<0$): $y=-1-x$
  • cuarto cuadrante ($x>0$, $y<0$): $y=-1+x$
Teniendo esto en cuenta, es fácil dibujar la región. Inténtalo y pulsa en 'Ver'.
Ver
La región que ocupa la placa es

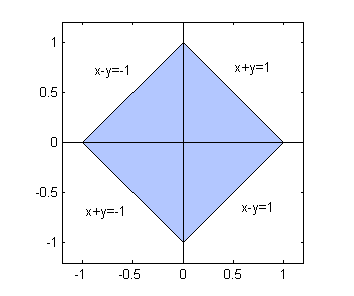
Gráfica

Esta figura, salvo las ecuaciones de los segmentos del contorno y el color, se ha dibujado con el siguiente código: 
 fill([-1 0 1 0],[0 -1 0 1],'g') %dibujo del cuadrado
 axis equal                         %  igual escala en los ejes
 hold on
 plot([-1.2 1.2],[0 0],'k')          % eje horizontal
 plot([0 0],[-1.2 1.2],'k')          % eje vertical
 axis([-1.2 1.2 -1.2 1.2])          % tamaño deseado para la caja
 hold off

Paso 2

¿Qué integral hemos de hacer? Según las interpretaciones de la integral doble, sabemos que el valor medio de la temperatura es $$T_m=\frac{\int\!\!\int_D T(x,y)\ dA}{\mbox{área(D)}}\ \ \ \mbox{en unidades de temperatura}$$ En este caso, el área de la placa es obviamente igual a 1 unidad de área. Para encontrar el valor de la integral del numerador, podemos
Opción A: escribir $$D=\{(x,y)/\, -1\leq x\leq 0,\, -1-x\leq y\leq 1+x\}\cup \{(x,y)/\, 0\leq x\leq 1,\, x-1\leq y\leq 1-x\}$$ y calcular después las correspondientes integrales iteradas
Ninguna de las dos opciones es razonable
Opción B: hacer un cambio de variable que simplifique el cálculo
Aunque las dos llevarían a la solución, es más conveniente la opción B que la A.
Es posible hacerlo así, pero es más recomendable un cambio de variable.
Hay un cambio de variable que simplifica mucho el cálculo.
Sí, las dos opciones son posibles, pero es más recomendable en este caso recurrir a un cambio de variable.
En efecto, aunque se pueda hacer directamente, en este caso exite un cambio de variable que facilita los cálculos. Piensa cuál puede ser y pulsa en 'Continuar'.
Puesto que las rectas que limitan la región son de la forma $x+y=\mbox{cte}$ o $x-y=\mbox{cte}$ el cambio adecuado es $$x+y=u \hspace{.4cm},\hspace{.5cm} x-y=v$$

Paso 3

Teniendo en cuenta el teorema del cambio de variable, para calcular la integral utilizando estas nuevas variables debemos seguir los siguientes pasos
  1. Encontrar los límites de integración en las nuevas variables
  2. Demostrar que es un cambio biyectivo
  3. Calcular el jacobiano del cambio
  4. Expresar el integrando en las nuevas variables
  5. Evaluar la integral

Paso 3.1

Las rectas que acotan la región $D$ en el plano $XY$, por el cambio $$x+y=u \hspace{.4cm},\hspace{.5cm} x-y=v$$ se transforman en las siguientes rectas en el plano $UV$: $\ldots$ hazlo tú y pulsa en 'Ver'
Ver
$$x+y=1 \hspace{.5cm} \Rightarrow \hspace{.5cm} u=1$$ $$x-y=1 \hspace{.5cm} \Rightarrow \hspace{.5cm} v=1$$ $$x-y=-1 \hspace{.5cm} \Rightarrow \hspace{.5cm} v=-1$$ $$x+y=-1 \hspace{.5cm} \Rightarrow \hspace{.5cm} u=-1$$ por lo que la región en el plano $UV$ es el cuadrado $$D^*=\{(u,v)/\, -1\leq u\leq 1,\, -1\leq v\leq 1\}$$

Paso 3.2

El cambio es biyectivo porque
  • es inyectivo: si dos puntos $(x,y)$ y $(x',y')$ del plano $XY$ son tales que $$x+y=x'+y' \hspace{.5cm} \mbox{y} \hspace{.5cm} x-y=x'-y'$$ entonces, sumando y restando estas expresiones, sabemos que $$2x=2x' \hspace{.5cm} \mbox{y} \hspace{.5cm} 2y=2y'$$ con lo cual $$x=x' \hspace{.5cm} \mbox{e} \hspace{.5cm} y=y'$$
  • es suprayectivo: cualquier punto $(u,v)$ del cuadrado $D^*$ puede escribirse como la imagen de un punto $(x,y)$ de $D$, ya que si $x+y=u$ y $x-y=v$, entonces $$x=\frac{1}{2}(u+v)\hspace{.3cm},\hspace{.5cm} y=\frac{1}{2}(u-v)$$

Paso 3.3

Debemos ahora calcular el jacobiano del cambio; el que debe introducirse en la integral es $\ldots$
$$\frac{\partial(u,v)}{\partial(x,y)}=\left|\begin{array}{ll} u'_x & u'_y \\ v'_x & v'_y \end{array}\right|$$
$$\frac{\partial(x,y)}{\partial(u,v)}=\left|\begin{array}{ll} x'_u & x'_v \\ y'_u & y'_v \end{array}\right|$$
No, ése no es el jacobiano que debe introducirse en la integral, puesto que pasamos de las variables $(x,y)$ a las variables $(u,v)$.
Sí, ése es el jacobiano que debe introducirse en la integral, puesto que pasamos de las variables $(x,y)$ a las variables $(u,v)$. Pero también es cierto que para calcularlo podemos hacer las derivadas parciales de $u$ y $v$ respecto de $x$ e $y$, ya que $$\frac{\partial(x,y)}{\partial(u,v)}=\frac{1}{\frac{\partial(u,v)}{\partial(x,y)}}$$ De esta forma es fácil obtener que $$\frac{\partial(x,y)}{\partial(u,v)}=\frac{1}{\left|\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right|}=-\frac{1}{2}$$

Paso 3.4

En la función del integrando la $x$ y la $y$ aparecen combinadas como $x+y$, así que es fácil escribirla en función de $u$ y $v$: $$f(x,y)=e^{x+y} \hspace{.5cm} \Rightarrow \hspace{.5cm} f(u,v)=e^u$$

Paso 3.5

Con todo esto, la integral que resulta es
$$\int\!\!\int_{D^*} e^u \frac{\partial(x,y)}{\partial(u,v)} dv\, du=-\frac{1}{2}\int_{-1}^1\int_{-1}^1 e^u \, dv\, du$$
La propuesta que se presenta tiene algún error.
No, revisa ese cálculo.
En efecto, el jacobiano debe introducirse en valor absoluto, pues $$dx\, dy\neq \frac{\partial(x,y)}{\partial(u,v)} dv\, du$$ sino que $$dx\, dy=\left| \frac{\partial(x,y)}{\partial(u,v)}\right| dv\, du $$ Por tanto, la integral es $$\int\!\!\int T(x,y)\, dA=\frac{1}{2}\int_{-1}^1\int_{-1}^1 e^u \, dv\, du= \frac{1}{2}\int_{-1}^1 e^u\, du \int_{-1}^1 dv=e-e^{-1}$$ Ya que el área de $D$ es 1, el valor medio de la temperatura en la placa es $e-e^{-1}$, medido en unidades de temperatura.