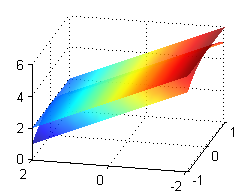
Enunciado
Tomamos \(f(x,y)=4-x^2-y\) y los rectángulos \(R_1=[-1,1]\times[-2,2]\) y \(R_2=[2,5]\times[1,3]\). Sin calcularlos, ordena de mayor a menor los siguientes números: $$I=\int\int_ {R_1} f(x,y)\, dA\ \ ,\ \ \ J=\int\int_ {R_2} f(x,y)\, dA\ \ ,\ \ \ K=\int\int_ {R_1} (4-y)\, dA$$
Paso 1
Observamos en primer lugar que la integral \(I\) y la \(J\) tienen el mismo integrando. Por tanto, teniendo en cuenta las propiedades de la integral doble, debemos estudiar cómo es esa función del integrando en los respectivos rectángulos de integración. Para ello analizamos el signo de \(f(x,y)=4-x^2-y\), hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
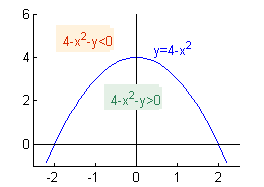
$$f(x,y)=4-x^2-y\geq 0 \ \ \ \ \Rightarrow \ \ \ \ y\leq 4-x^2$$
En los puntos de la parábola \(y=4-x^2\), la función \(f(x,y)\) es nula; por encima de la parábola es negativa y por debajo es positiva:
Paso 2
¿Dónde se encuentra el rectángulo \(R_1=[-1,1]\times[-2,2]\) respecto de la parábola \(y=4-x^2\)? Piénsalo y pulsa en 'Ver'
Ver
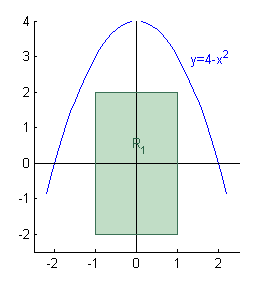
Los vértices superiores de \(R_1=[-1,1]\times[-2,2]\), que son \((-1,2)\) y \((1,2)\), están por debajo de la parábola, por tanto en todo \(R_1\) la función \(f(x,y)\) es positiva. De donde deducimos que ... piénsalo y pulsa en 'Continuar'.
La integral \(I\) es positiva.
Paso 3
Hacemos ahora el mismo análisis para el rectángulo \(R_2=[2,5]\times[1,3]\). ¿Qué podemos deducir? piénsalo y pulsa en 'Ver'
Ver
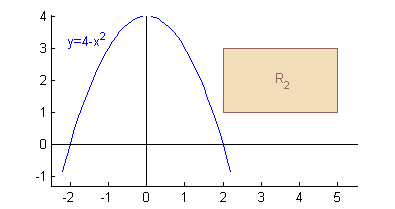
El vértice izquierdo de \(R_2=[2,5]\times[1,3]\), que es \((2,1)\) está encima de la parábola, por tanto en todo \(R_2\) la función \(f(x,y)\) es negativa. De donde deducimos que la integral \(J\) es negativa y por tanto ya tenemos la relación $$I>J$$
Paso 4
Observamos ahora que la región de integración de \(K\) es la misma que la de \(I\). Eso quiere decir que lo que habrá que comparar son los integrandos, para utilizar la propiedad de acotación. Piénsalo y pulsa en 'Ver'
Ver
Es claro que $$4-y> 4-x^2-y$$ en cualquier parte del plano, en particular sobre la región de integración. Por tanto, haciendo uso de la propiedad de acotación,
$$K>I$$
Tratándose $z=4-y$ de una función positiva en todo el rectángulo $R_1$, podemos interpretar $K$ como el volumen de la región que queda bajo su gráfica y sobre el rectángulo $R_1$. Obviamente este volumen es mayor que el de la región que queda por debajo de la gráfica de $z=4-x^2-y$ sobre el mismo rectángulo.