Índice de tema

 

Enunciado

Sea $R=[-1,2]\times[0,2]$ y $z=f(x,y)=\cos(x^2)+\cos(xy^2)$
    • Escribe las líneas con las que, en el ordenador, hallas la suma de Riemann correspondiente a tomar una partición de $R$ en $6\times 4$ subrectángulos, evaluando la función en los puntos medios de cada uno de los subrectángulos.
    • Compara el resultado obtenido con el valor que el ordenador devuelve utilizando el comando int del paquete simbólico.
    • Genera una función, llámala intdobleaprox, que tenga como variables de entrada el número de subintervalos de $[-1,2]$, sea $n$, y el número de subintervalos de $[0,2]$, sea $m$. La salida de esta función debe ser la suma de Riemann de las mismas características de la anterior.
    • Prueba intdobleaprox con valores de $n$ y $m$ distintos de 6 y 4 y compara con el resultado que se obtuvo utilizando int.
    • ¿Y si el rectángulo no es $[-1,2]\times[0,2]$? Modifica intdobleaprox con objeto que sirva para un rectángulo genérico de la forma $[a,b]\times[c,d]$.
    • Añade también el cálculo simbólico de la integral doble correspondiente y la comparación de ambos resultados, incluyendo como variable de salida la diferencia entre el valor aproximado y el simbólico.
  4. Finalmente, modifica intdobleaprox para que sirva para cualquier función $z=f(x,y)$.

Resolución del primer apartado

Paso 1

Establecer la suma que ha de calcularse. En este caso, estamos tomando la definición de suma de Riemann para una partición en que todos los subrectángulos son de igual área. ¿Cuáles son las dimensiones de cada subrectángulo? Piénsalo y pulsa en 'Ver'.
Ver
El intervalo $[-1,2]$ se divide en 6 subintervalos iguales, luego cada uno tendrá longitud $\Delta x=0.5$; el intervalo $[0,2]$ se divide en 4 subintervalos, así que también $\Delta y=0.5$. El área de cada subrectángulo de la partición es $\Delta A=0.25$. Por tanto la suma de Riemann que hemos de calcular será $$S=0.25\sum_{k=1}^{24} f(x_k,y_k)$$ siendo $(x_k,y_k)$ el punto medio de cada subrectángulo.

Paso 2

Escribir los puntos $(x_k,y_k)$ sobre los que se evalúa la función. En la siguiente figura puedes verlos marcados en verde.

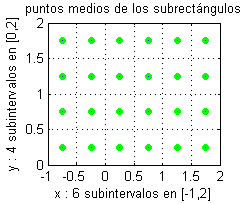
Gráfica

El punto medio del subrectángulo $R_1=[-1,-0.5]\times[0,0.5]$ es $P_1=(-0.75,0.25)$. Así podemos ver que
  • las abscisas de esos puntos medios comenzarán en $-0.75$ y estarán distanciadas $\Delta x=0.5$ hasta llegar a $1.75$;
  • las ordenadas de los puntos medios comenzarán en $0.25$ y, distanciadas $\Delta y=0.5$, llegarán a $1.75$.
Ahora ya tenemos toda la información para pedirle al ordenador que calcule esa suma de Riemann.

Paso 3

Escribir las líneas para calcular esa suma de Riemann: en cada fase piénsalo y pulsa en 'Continuar'
  • define un vector con las abscisas de los puntos medios: 
x=-.75:.5:1.75;
  • define un vector con las ordenadas de los puntos medios: 
y=.25:.5:1.75;
  • genera una malla con los puntos de los vectores x e y: 
[X,Y]=meshgrid(x,y);
  • define una matriz con los valores $f(x_k,y_k)$: 
Z=cos(X.^2)+cos(X.*Y.^2);
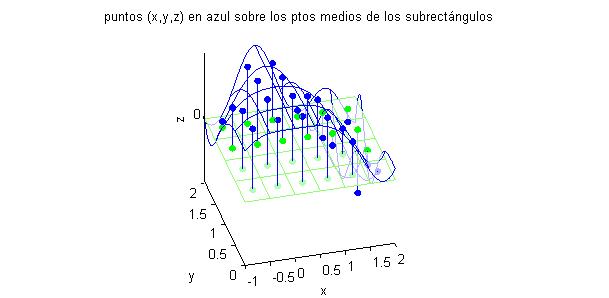
Los valores de esta matriz Z son las terceras componentes de los puntos azules de la siguiente figura Gráfica
  • suma los valores de la matriz Z multiplicados por $\Delta A=0.25$: 
.25*sum(Z(:))
El resultado de ejecutar todas las líneas que hemos ido escribiendo: 
x=-.75:.5:1.75; 			% abscisas de los puntos medios
y=.25:.5:1.75; 				% ordenadas de los puntos medios
[X,Y]=meshgrid(x,y); 		% malla de puntos medios
Z=cos(X.^2)+cos(X.*Y.^2);   % valores de la función en los puntos medios
.25*sum(Z(:)) 				% suma de Riemann
es $5.7963$. Este valor es la suma de los 'volúmenes' (con signo negativo si la tercera componente del punto azul es negativa):

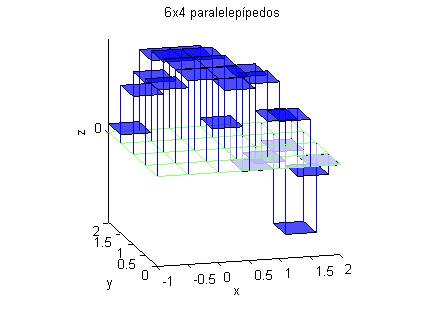
Gráfica

Debemos compararlo con el valor obtenido utilizando el comando int del paquete simbólico: 
syms xs ys % declaramos xs e ys como variables simbólicas
double(int(int(cos(xs^2)+cos(xs*ys^2),xs,-1,2),ys,0,2)) % cálculo de las dos integrales iteradas
el valor obtenido así es $5.8049$. Este valor es el 'volumen' que queda entre la gráfica de $z=f(x,y)$ en $R$ y el plano $z=0$, entendiendo que lo que aporta la parte que está en $z<0$ es un número negativo:

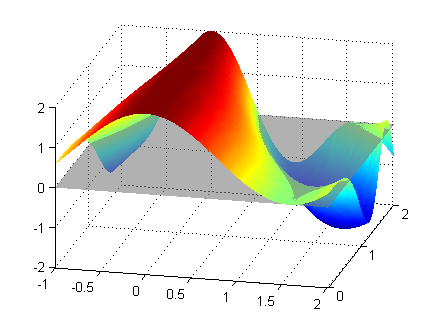
Gráfica

Resolución del segundo apartado

El número de subintervalos tomados en $[-1,2]$ y en $[0,2]$ es ahora variable; por tanto, los tamaños $\Delta x$ y $\Delta y$, que son también las distancias en horizontal y vertical de los puntos medios sobre los que se evalúa la función, deberán ser calculados dentro de la función intdobleaprox. Escribimos esa función siguiendo las siguientes fases:
  • define intdobleaprox como función, con sus variables de entrada y de salida; recuerda que el fichero .m donde escribas esta función debe llamarse intdobleaprox.m: 
function s=intdobleaprox(n,m)
  • genera un vector con los dos incrementos, $\Delta x$ y $\Delta y$, teniendo en cuenta las longitudes de $[-1,2]$ y de $[0,2]$:
h=[3 2]./[n m];
  • genera un vector con las abscisas de los puntos medios:
x=-1+h(1)/2:h(1):2-h(1)/2;
  • genera un vector con las ordenadas de los puntos medios:
y=h(2)/2:h(2):2-h(2)/2;
  • genera una malla con los puntos medios y una matriz con los valores de f en ella:
[X,Y]=meshgrid(x,y);
Z=cos(X.^2)+cos(X.*Y.^2);
  • calcula la suma de Riemann (ten en cuenta que $\Delta A=\Delta x\Delta y$), llámala s y termina la función:
s=prod(h)*sum(Z(:));
end
Escritas todas las líneas seguidas resulta 
function s=intdobleaprox(n,m)  % declaración de función
h=[3 2]./[n m];                % cálculo de los incrementos
x=-1+h(1)/2:h(1):2-h(1)/2;     % abscisas de los puntos medios
y=h(2)/2:h(2):2-h(2)/2;		   % ordenadas de los puntos medio
[X,Y]=meshgrid(x,y);           % malla de puntos medios
Z=cos(X.^2)+cos(X.*Y.^2);	   % valores de f sobre la malla
s=prod(h)*sum(Z(:));           % suma de Riemann
end							   % fin de la función
Si en la ventana de comandos ejecutamos 
>> s=intdobleaprox(12,8)
obtendremos $s= 5.8045$, que se aproxima más al valor obtenido en simbólico.

Resolución del tercer apartado

¿Qué se ha de cambiar en la función intdobleaprox escrita arriba para nos sirva para cualquier rectángulo? Cambiarán $\ldots$
sólo una línea
tres líneas
más de cuatro líneas
cuatro líneas
Debe cambiarse más de una línea
Deben cambiarse más de tres líneas
No deben cambiarse más de cuatro líneas
Deben cambiarse cuatro líneas: la definición de la función, el cálculo de los incrementos y las definiciones de abscisas y ordenadas de los puntos medios. Realiza esos cambios y pulsa en 'Continuar'.
La función modificada es 
function s=intdobleaprox(a,b,c,d,n,m) % declaración de función
h=[b-a d-c]./[n m];						% cálculo de los incrementos
x=a+h(1)/2:h(1):b-h(1)/2;				% abscisas de los puntos medios
y=c+h(2)/2:h(2):d-h(2)/2;				% ordenadas de los puntos medio
[X,Y]=meshgrid(x,y);					% malla de puntos medios
Z=cos(X.^2)+cos(X.*Y.^2);				% valores de f sobre la malla
s=prod(h)*sum(Z(:));					% suma de Riemann
end									% fin de la función
Ahora debemos adaptarla para que dé como salida también la diferencia entre el valor aproximado (suma de Riemann) y el valor calculado con el paquete simbólico.
  1. cambiamos la declaración de la función 
    function [s, dif]=intdobleaprox(a,b,c,d,n,m)
  2. añadimos las líneas del cálculo de la integral y de la diferencia 
    syms xs ys
intex=double(int(int(cos(xs^2)+cos(xs*ys^2),xs,a,b),ys,c,d))
dif=abs(s-intex);
La nueva función será 
function [s, dif]=intdobleaprox(a,b,c,d,n,m)   % declaración de función
h=[b-a d-c]./[n m];						% cálculo de los incrementos
x=a+h(1)/2:h(1):b-h(1)/2;				% abscisas de los puntos medios
y=c+h(2)/2:h(2):d-h(2)/2;				% ordenadas de los puntos medio
[X,Y]=meshgrid(x,y);					% malla de puntos medios
Z=cos(X.^2)+cos(X.*Y.^2);				% valores de f sobre la malla
s=prod(h)*sum(Z(:));					% suma de Riemann
syms xs ys 							% declaramos xs e ys como variables simbólicas
intex=double(int(int(cos(xs^2)+cos(xs*ys^2),xs,a,b),ys,c,d)) % cálculo de las dos integrales iteradas
dif=abs(s-intex);						% cálculo de la diferencia
end										% fin de la función

Resolución del cuarto apartado

Finalmente debemos modificar esta función de manera que sirva para cualquier función $z=f(x,y)$. En una primera opción modificaremos la función que da únicamente la aproximación, sin incluir el cálculo de la exacta con el paquete simbólico. Después modificaremos la versión de intdobleaprox que sí incluía ese cálculo.
  • Poder ejecutar intdobleaprox para una función $f$ genérica significa incorporar otra variable de entrada en la definición de intdobleaprox; la función se introducirá como un string (cuando se ejecute intdobleaprox, esta primera variable deberá ir entre comillas simples) 
    function s=intdobleaprox(f,a,b,c,d,n,m)
    Las líneas de preparación de la malla permanecerán igual, y sólo habrá que modificar la línea en la que se evalua la función sobre la malla, para lo cual hay que vectorizarla previamente: 
    f=vectorize(inline(f));
Z=f(X,Y);
    La función completa será: 
    function s=intdobleaprox(f,a,b,c,d,n,m) % declaración de función
h=[b-a d-c]./[n m];				% cálculo de los incrementos
x=a+h(1)/2:h(1):b-h(1)/2;		% abscisas de los puntos medios
y=c+h(2)/2:h(2):d-h(2)/2;		% ordenadas de los puntos medio
[X,Y]=meshgrid(x,y);			% malla de puntos medios
f=vectorize(inline(f));			% se vectoriza la función
Z=f(X,Y);						% valores de f sobre la malla
s=prod(h)*sum(Z(:));			% suma de Riemann
end								% fin de la función
    Si ahora ejecutamos, desde la ventana de comandos, 
     s=intdobleaprox('x*y',-1,2,0,2,20,10)
    el programa nos devolverá $3.000$, que es el valor de la suma de Riemann para $z=xy$ en el rectángulo $R=[-1,2]\times[0,2]$ con una partición de $20\times10$ rectángulos, evaluando la función en los puntos medios de cada subrectángulo.
  • ¿Y cómo hacemos para incorporar el cálculo de la integral utilizando simbólico? Una opción es introducir la función genérica en simbólico. Para ello, antes de ejecutar intdobleaprox tendremos que haber declarado antes dos variables simbólicas. Veamos primero qué modificaciones deben hacerse en el fichero intdobleaprox.m y después ya nos ocuparemos de cómo ejecutar intdobleaprox.
    • En la declaración de la función volveremos a incorporar la diferencia, dif, que queremos como variable de salida y la función,f, que queremos como nueva variable de entrada: 
      function [s,dif]=intdobleaprox(f,a,b,c,d,n,m)
      y para que pueda evaluar la función sobre los puntos de la malla, antes de vectorizar hemos de pasarla a tipo carácter: 
      f=vectorize(inline(char(f)));
Z=f(X,Y);
      Así, el programa resultaría 
      function [s,dif]=intdobleaprox(f,a,b,c,d,n,m)% declaración de función
syms xs ys					% declaramos xs e ys como variables simbólicas
intex=double(int(int(f,xs,a,b),ys,c,d))% cálculo de las dos integrales iteradas
h=[b-a d-c]./[n m];			% cálculo de los incrementos
x=a+h(1)/2:h(1):b-h(1)/2;	% abscisas de los puntos medios
y=c+h(2)/2:h(2):d-h(2)/2;	% ordenadas de los puntos medio
[X,Y]=meshgrid(x,y);		% malla de puntos medios
f=vectorize(inline(char(f)));% se vectoriza la función
Z=f(X,Y);					% valores de f sobre la malla
s=prod(h)*sum(Z(:));		% suma de Riemann
dif=abs(s-intex); 			% cálculo de la diferencia
end							% fin de la función
    • Una vez así construida, para ejecutarla pondremos en la ventana de comandos 
      syms xs ys
[s,int]=intdobleaprox(xs*ys,-1,2,0,2,20,10)