Integración múltiple

Cambio de variables

TEOREMA (Cambio de variable en una integral doble).

Hipótesis:

$\bullet $ las regiones $R$ y $D$ de los planos $XY$ y $ST$ respectivamente, están relacionadas por las ecuaciones $$x = x(s,t)\;\;,\;\;y = y(s,t)$$

$\bullet $ esa relación entre $R$ y $D$ es biyectiva (cada punto de $R$ es imagen de uno y sólo un punto de $D$).

$\bullet $ las funciones del cambio, $x(s,t)$ e $y(s,t)$ , admiten derivadas parciales continuas en $D$.

$\bullet $ la función es continua en la región R.

Tesis: $$\int \int_R \,f(x,y){\kern 1pt} dx{\kern 1pt} dy = \int \int_D \,f(x(s,t),y(s,t)){\kern 1pt} \left| {{{\partial (x,y)} \over {\partial (s,t)}}} \right|ds{\kern 1pt} dt$$ siendo, $${{\partial (x,y)} \over {\partial (s,t)}} = \left| {\matrix{
{{{x'}_s}} & {{{x'}_t}} \cr
{{{y'}_s}} & {{{y'}_t}} \cr

} } \right|$$

OBSERVACIONES

El factor $J = {{\partial (x,y)} \over {\partial (s,t)}}$ se llama jacobiano del cambio

El valor absoluto del jacobiano da la relación entre un elemento diferencial de área del plano $XY$ y un elemento diferencial del plano $ST$: $$dx{\kern 1pt} dy = |J|{\kern 1pt} ds{\kern 1pt} dt$$ Puesto que tanto $dx{\kern 1pt} dy$ como $ds{\kern 1pt} dt$ son positivos, el cociente entre ellos es positivo: recuerda que el jacobiano siempre se introduce en la integral en valor absoluto.

Si el cambio de variables fuera el inverso, es decir, el que escribe las coordenadas $s$ y $t$ en función de $x$ e $y$ , entonces el jacobiano sería el inverso, es decir $$\,{{\partial (s,t)} \over {\partial (x,y)}} = {1 \over {{{\partial (x,y)} \over {\partial (s,t)}}}}$$

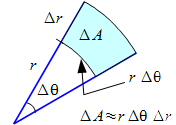
Cambio de coordenadas a polares

Este es uno de los cambios de variables más habituales. Las fórmulas del cambio son $$x = r{\kern 1pt} \cos\theta \;\;,\;\;y = r{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta $$ establecidas de forma biyectiva entre dos conjuntos $S$ y $R$, siendo $r$ positiva.

Esquema polares

El jacobiano es $$J = {{\partial (x,y)} \over {\partial (r,\theta )}} = \left| {\matrix{ {\cos \theta } {\kern 4pt}{ - r{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta } \cr {{\kern 1pt} \mbox{sen}{\kern 1pt} {\kern 1pt} \theta } {{\kern 4pt}r\cos \theta } \cr } } \right| = r$$ Resultando, $$\int \int_R \,f(x,y){\kern 1pt} dx{\kern 1pt} dy = \int \int_S \,f(r\cos \theta ,r{\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta ){\kern 1pt} r{\kern 1pt} dr{\kern 1pt} d\theta $$