Enunciado
Se considera la ecuación
$$x^2\frac{d^2y}{dx^2}-4x\frac{dy}{dx}+6y=x^3$$ en el dominio $x>0$.
- Comprueba que el cambio de variable independiente $$x=e^t$$ transforma la ecuación en una de coeficientes constantes.
- Encuentra la solución general de la ecuación transformada (funciones $y(t)$) y la solución general de la inicial (funciones $y(x)$).
- Halla la familia de soluciones $y(x)$ que pasan por el punto $P(1,2)$. Representa una muestra con el ordenador en el intervalo $[0.5,1.5]$. ¿Cuál es la familia correspondiente en las funciones $y(t)$?
- Halla la familia de soluciones $y(x)$ que tienen pendiente $-1/2$ en los puntos de la forma $(1,y(1))$. Representa una muestra en el intervalo $[0.5,1.5]$ con el ordenador. ¿Cuál es la familia correspondiente en las funciones $y(t)$?
- Determina y representa la solución $y(x)$ que cumple las dos condiciones que determinan las familias de los dos apartados anteriores. ¿Cuál es su correspondiente $y(t)$?
Resolución del primer apartado
Paso 1
Hemos de escribir la ecuación diferencial en términos de $t$, $y(t)$ y las derivadas de $y(t)$ respecto de $t$. Para ello hay que saber cómo expresar las derivadas de $y$ respecto de $x$ en función de las derivadas de $y$ respecto de $t$: para ello basta aplicar la regla de la cadena o regla de la derivación compuesta, considerando que $y$ es función de $t$ que a su vez es función de $x$: $$\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$$ pero puesto que $x=e^t$, $$\frac{dy}{dx}=\frac{dy}{dt}e^{-t}$$ Observa que hemos de dejar todos los factores de la derivada escritos en función de $t$. Ahora haz tú lo mismo para la segunda derivada, teniendo en cuenta que la segunda derivada no es otra cosa que la derivada de la derivada. Pulsa en 'Ver' cuando lo tengas.
Ver
$$\frac{d^2y}{dx^2}\stackrel{(1)}{=}\frac{d}{dx}\left(\frac{dy}{dx}\right)\stackrel{(2)}{=}\frac{d}{dt}\left(\frac{dy}{dx}\right)\frac{dt}{dx}\stackrel{(3)}{=}\frac{d}{dt}\left(\frac{dy}{dt}e^{-t}\right)e^{-t}\stackrel{(4)}{=}$$
$$\stackrel{(4)}{=}\left(\frac{d^2y}{dt^2}e^{-t}-\frac{dy}{dt}e^{-t}\right)e^{-t}\stackrel{(5)}{=}\left(\frac{d^2y}{dt^2}-\frac{dy}{dt}\right)e^{-2t}$$
donde hemos aplicado
- en (1): que la derivada segunda es la derivada de la primera
- en (2): la regla de la derivación compuesta, para derivar respecto de $x$ hemos de derivar respecto de $t$ y multiplicar por la derivada de $t$ respecto de $x$
- en (3): que ya conocemos $dy/dx$ en función de $t$ y la $dt/dx$
- en (4): la derivada de un producto
- en (5): sacar factor común
Paso 2
Ahora hemos de cambiar en la ecuación inicial las expresiones de $x$ por sus correspondientes en $t$, es decir $$x=e^t \hspace{.5cm},\hspace{.5cm} \frac{dy}{dx}=\frac{dy}{dt}e^{-t} \hspace{.5cm},\hspace{.5cm} \frac{d^2y}{dx^2}=\left(\frac{d^2y}{dt^2}-\frac{dy}{dt}\right)e^{-2t}$$ hazlo tú y pulsa en 'Ver'.
Ver
Al hacer esas sustituciones y simplificar, se obtiene la ecuación diferencial
$$\frac{dy^2}{dt^2}-5\frac{dy}{dt}+6y=e^{3t}$$
que está definida en todos los reales y es lineal de coeficientes constantes.
Resolución del segundo apartado
Construiremos la solución general de esta última ecuación como suma de la solución general de la homogénea asociada más una solución particular de la completa.Paso 1
Encontrar la solución general de la homogénea asociada: $$y''_h-5y'_h+6y_h=0$$ Hallando las raíces de la ecuación característica, sabemos que ...
$$y_h(x)=C_1e^{-2x}+C_2e^{3x}$$
$$y_h(x)=C_1e^{2x}+C_2e^{3x}$$
Ninguna es correcta.
No es correcta.
No es correcta, las raíces están bien calculadas, pero hemos de mantener el nombre de la variable, pues $x$ es otra variable que existe, diferente de $t$.
En efecto, la solución general de la homogénea asociada es
$$y_h(t)=C_1e^{2t}+C_2e^{3t}$$
Paso 2
Hallar una solución particular de la ecuación completa $$y''(t)-5y'(t)+6y(t)=e^{3t}$$ Podemos hacerlo por cualquiera de los dos métodos: método de variación de constantes o método de los coeficientes indeterminados. Consideramos el segundo más apropiado, por la sencillez del término independiente. Así pues, hemos de proponer una forma para la solución particular, podría ser...
$$y_p(t)=Ae^{3t}$$
Ninguna es correcta.
$$y_p(t)=(At+B)e^{3t}$$
$$y_p(t)=Ate^{3t}$$
Pero si esa función es solución de la homogénea, no puede ser solución de la completa.
Sí hay una correcta.
No hace falta poner el sumando $Be^{3t}$, pues es solución de la homogénea.
En efecto, esa es la forma adecuada para $y_p(t)$. Ahora debes derivar y sustituir en la ecuación para determinar el valor de $A$. Pincha en 'Continuar' cuando lo tengas.
$$y_p(t)=Ate^{3t} \hspace{.5cm}\Rightarrow \hspace{.5cm}
y'_p(t)=Ae^{3t}(1+3t)
\hspace{.5cm}\Rightarrow \hspace{.5cm} y''_p(t)=Ae^{3t}(6+9t)$$
con lo cual
$$y''_p(t)-5y''_p(t)+6y_p(t)=Ae^{3t}=e^{3t} \hspace{.5cm}\Rightarrow \hspace{.5cm} A=1
\hspace{.5cm}\Rightarrow \hspace{.5cm} y_p(t)=te^{3t}$$
y por tanto la solución general de la completa es
$$y(t)=C_1e^{2t}+C_2e^{3t}+te^{3t}$$
A partir de aquí, deshaciendo el cambio de variable, encontramos la solución general de la ecuación en $y(x)$. Pulsa en 'Ver' cuando la tengas.
Ver
$$e^t=x\hspace{.5cm}\Rightarrow \hspace{.5cm} y(x)=C_1x^2+C_2x^3+x^3\log x$$
es la solución general de la ecuación inicial, formada por funciones definidas en $x>0$.
Resolución del tercer apartado
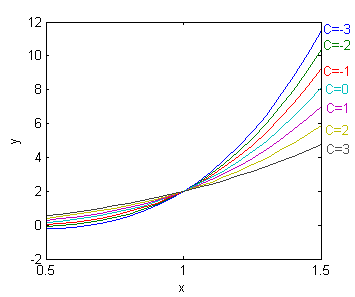
Las soluciones que pasan por el punto $P(1,2)$, deben cumplir que $y(1)=2$, es decir, $$C_1+C_2=2$$ así que podemos expresarlas como la familia $$y(x)=Cx^2+(2-C)x^3+x^3\log x$$ de funciones definidas en $x>0$. Representamos una muestra (las correspondientes a $C$ desde $-3$ a $3$ con paso 1) con el código
c=-3:3;
x=0.5:.05:1.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2+(2-C).*X.^3+X.^3.*log(X);
plot(x,Y)
xlabel('x');ylabel('y')
Ver
Serán las funciones $$y(t)=C_1e^{2t}+(2-C_1)e^{3t}+te^{3t}$$ definidas para cualquier $t$ real y cuyas gráficas pasan por el punto $(0,2)$ del plano (T,Y).
Resolución del cuarto apartado
Hemos de hallar ahora las soluciones que tienen pendiente $-1/2$ cuando cortan al eje $x=1$, es decir, las que cumplen que $y'(1)=-1/2$. Debemos derivar la expresión de la solución general $$y(x)=C_1x^2+C_2x^3+x^3\log x$$ e imponerle esa condición. Hazlo tú y pulsa en 'Ver' cuando tengas la familia de funciones.
Ver
La derivada de la solución general es
$$y'(x)=2C_1x+3C_2x^2+x^2(3\log x+1)$$
De imponer que $y'(1)=-1/2$, se obtiene que $$2C_1+3C_2=-\frac{3}{2}$$ y así sabemos que la familia de soluciones con pendiente $-1/2$ en los puntos $(1,y(1))$ se puede escribir como
$$y(x)=Cx^2-\frac{1}{3}(\frac{3}{2}+2C)x^3+x^3\log x$$
definidas en $x>0$.
Representamos una muestra (las correspondientes a $C$ desde $-3$ a $3$ con paso 1) con el código
c=-3:3;
x=0.5:.05:1.5;
[X,C]=meshgrid(x,c);
Y=C.*X.^2-(3/2+2*C).*X.^3/3+X.^3.*log(X);
plot(x,Y)
grid on
xlabel('x');ylabel('y')
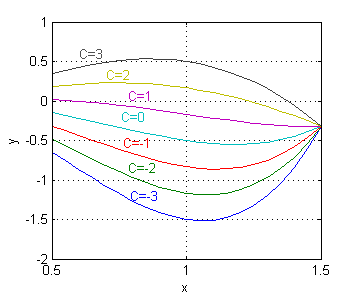
Resolución del quinto apartado
Debemos determinar la función que forma parte a la vez de las familias $$y(x)=Cx^2+(2-C)x^3+x^3\log x \hspace{.5cm}\mbox{e}\hspace{.5cm} y(x)=Cx^2-\frac{1}{3}(\frac{3}{2}+2C)x^3+x^3\log x$$ Si imponemos que el coeficiente de la $x^2$ sea el mismo, deberá cumplirse que $$2-C=-\frac{1}{3}(\frac{3}{2}+2C)$$ (también puedes hacerlo imponiendo que una de la segunda familia cumpla que $y(1)=2$). Encuentra la función y escribe el código para representarla; pulsa en 'Ver' después.
Ver
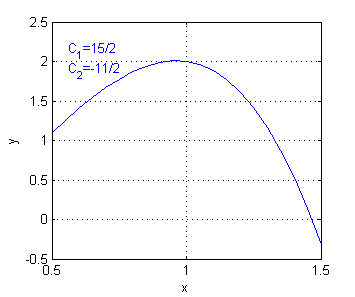
$$2-C=-\frac{1}{3}(\frac{3}{2}+2C) \hspace{.5cm} \Rightarrow \hspace{.5cm} C=\frac{15}{2}$$
La función buscada es
$$y(x)=\frac{15}{2} x^2-\frac{11}{2} x^3+x^3\log x$$
definida en $x>0$. La representamos en el intervalo $[0.5,1.5]$ con
x=0.5:.05:1.5;
plot(x,15*x.^2/2-11*x.^3/2+x.^3.*log(x))
grid on
xlabel('x');ylabel('y')