Enunciado
Dada la ecuación lineal de segundo orden
$$y''+y=2x\,\mbox{sen}\, x$$
- Encuentra la solución general de la homogénea asociada.
- Halla su solución general, utilizando el método de variación de constantes.
- Determina la solución que pasa por el punto $P(0,1)$, formando su recta tangente un ángulo de $3\pi/4$ radianes, en ese punto, con el eje horizontal positivo. Represéntala en el ordenador, primero para $x$ en $[-\pi/6,\pi/6]$, luego en el intervalo $[-2\pi,2\pi]$ y finalmente en $[-4\pi,4\pi]$.
Resolución del primer apartado
La ecuación homogénea asociada es $$y''_h+y_h=0$$ se trata de una ecuación lineal de segundo orden con coeficientes constantes y homogénea.
Paso 1
Escribir su ecuación característica:
$$r^2+r=0$$
Ninguna de las dos opciones es correcta.
$$r^2+1=0$$
No, fíjate bien.
Sí hay una correcta.
Esa es la ecuación característica correcta.
Paso 2
Calculamos las raíces de esta ecuación y formamos la solución general. Hazlo tú y pulsa en 'Continuar'.
Las raíces son $r_1=i$ y $r_2=-i$, luego las soluciones del sistema fundamental son
$$y_1(x)=\cos x \hspace{.5cm} \mbox{e} \hspace{.5cm} y_2(x)=\mbox{sen}\, x$$
y la solución general será la familia biparamétrica
$$y_h(x)=C_1\cos x+C_2\,\mbox{sen}\, x$$
Resolución del segundo apartado
La solución general de la ecuación completa es la suma de la solución general de la homogénea y una solución particular de la completa: $$y(x)=y_h(x)+y_p(x)$$ Del primer apartado conocemos el primer sumando, nos queda por tanto encontrar una solución particular de la completa; para este trabajo es para lo que usaremos el método de variación de constantes.Paso 1
Planteamos la solución particular $$y_p(x)=C_1(x)\cos x+C_2(x)\,\mbox{sen}\, x$$ con la condición añadida:
$$-C_1(x)\mbox{sen}\, x+C_2(x)\cos x=0$$
$$C'_1(x)\cos x+C'_2(x)\,\mbox{sen}\, x=1$$
$$C'_1(x)\cos x+C'_2(x)\,\mbox{sen}\, x=0$$
No es esa, fíjate bien.
No es esa, fíjate bien.
En efecto, esa es la condición que va a impedir que tengamos que manejar expresiones con las derivadas segundas de $C_1(x)$ y $C_2(x)$.
Paso 2
Deriva $y_p(x)$ dos veces y haz que cumpla la ecuación diferencial. Pulsa en 'Ver' cuando termines.
Ver
$$y_p(x)=C_1(x)\cos x+C_2(x)\,\mbox{sen}\, x \hspace{.3cm} \Rightarrow \hspace{.3cm}
y'_p(x)=C'_1(x)\cos x-C_1(x)\,\mbox{sen}\, x+C'_2(x)\,\mbox{sen}\, x +C_2(x) \cos x$$
pero puesto que $C'_1\cos x+C'_2\,\mbox{sen}\, x=0$, tendremos
$$y'_p(x)=-C_1(x)\,\mbox{sen}\, x+C_2(x) \cos x$$
Derivando de nuevo,
$$y''_p(x)=-C'_1(x)\,\mbox{sen}\, x-C_1(x)\cos x+C'_2(x) \cos x-C_2(x)\,\mbox{sen}\, x$$
Puesto que la función $y_p$ debe ser solución de la ecuación completa,
$$y''_p(x)+y_p(x)=2x\,\mbox{sen}\, x \hspace{.3cm} \Rightarrow \hspace{.3cm}
-C'_1(x)\,\mbox{sen}\, x+C'_2(x) \cos x=2x\,\mbox{sen}\, x$$
Paso 3
Debemos resolver el sistema $$\left\{\begin{array}{l} C'_1(x)\cos x+C'_2(x)\,\mbox{sen}\, x=0 \\ -C'_1(x)\,\mbox{sen}\, x+C'_2(x) \cos x=2x\,\mbox{sen}\, x \end{array}\right.$$ Hay muchas manera de encontrar $C'_1(x)$ y $C'_2(x)$; por ejemplo podemos multiplicar la primera ecuación por $\mbox{sen}\, x$, la segunda por $\cos x$ y sumarlas; tendremos $$C'_2(x)=2x\,\mbox{sen}\, x \cos x=x\,\mbox{sen}\, 2x$$ y utilizando la primera, $$C'_1(x)=-2x\,\mbox{sen}^2x $$Paso 4
Encontramos $C_1(x)$ y $C_2(x)$ mediante integración de sus derivadas. Para integrar $C'_1(x)$ escribimos el seno cuadrado en función del ángulo doble y aplicamos integración por partes; para encontrar $C_2(x)$ utilizamos también integración por partes. Inténtalas y pulsa en 'Ver' cuando la tengas.
Ver
$$C_1(x)=-2\int x\,\mbox{sen}^2x \, dx=-\int x(1-\cos 2x)\, dx=-\int x\, dx+\int x\cos 2x \, dx$$
Integrando por partes ($u=x$, $dv=\cos 2x\, dx$), tendremos
$$C_1(x)=-\frac{x^2}{2}+\frac{x}{2}\mbox{sen}\, 2x+\frac{1}{4}\cos 2x+C$$
Para $C_2(x)$,
$$C_2(x)=\int x\,\mbox{sen}\, 2x\, dx$$
integrando por partes ($u=x$, $dv=\mbox{sen}\, 2x\, dx$), tendremos
$$C_2(x)=-\frac{x}{2}\cos 2x+\frac{1}{4}\mbox{sen}\, 2x+C$$
Las constantes de integración podemos tomarlas como cero, puesto que sólo necesitamos una función $C_1(x)$ y una función $C_2(x)$.
Escribe cómo queda la solución particular de la completa y su solución general. Pulsa después en 'Continuar'.
Una solución particular de la completa es
$$y_p(x)=C_1(x)\cos x+C_2(x)\,\mbox{sen}\, x=$$
$$=-\frac{x^2}{2}\cos x+\frac{x}{2}\mbox{sen}\, 2x\cos x+\frac{1}{4}\cos 2x\cos x-
\frac{x}{2}\cos 2x\,\mbox{sen}\, x+\frac{1}{4}\mbox{sen}\, 2x\,\mbox{sen}\, x
$$
pero teniendo en cuenta que $\cos 2x=\cos^2x-\mbox{sen}^2x$, $\mbox{sen}\, 2x=2\,\mbox{sen}\, x\cos x$, $\cos^2 x=1-\,\mbox{sen}^2x$, $\mbox{sen}^2x=1-\cos^2x$,
$$y_p(x)=-\frac{x^2}{2}\cos x+\frac{1}{4}\cos x+\frac{1}{2}x\, \mbox{sen}\, x$$
y por tanto la solución general de la ecuación completa es
$$y(x)=C_1\cos x+C_2\,\mbox{sen}\, x+\frac{x}{2}\,\mbox{sen}\, x-\frac{x^2}{2}\cos x$$
(el factor $\frac{1}{4}\cos x$ que aparece en la solución particular se engloba en $C_1\cos x$).
Resolución del tercer apartado
Se pide ahora la solución particular de la ecuación $$y''+y=2x\,\mbox{sen}\, x$$ que pasa por el punto $P(0,1)$, formando su recta tangente en ese punto un ángulo de $3\pi/4$ radianes con el eje horizontal positivo. La solución particular calculada antes no nos sirve, pues pasa por el punto $(0,1/4)$, no por el punto $(0,1)$. Pero sí sabemos que debe ser una de la familia $$y(x)=C_1\cos x+C_2\,\mbox{sen}\, x+\frac{x}{2}\,\mbox{sen}\, x-\frac{x^2}{2}\cos x$$ Empezamos imponiendo que $y(0)=1$: $$y(0)=C_1=1$$ ¿Cómo haremos para determinar el valor de $C_2$? Piénsalo y pulsa en 'Ver'.
Ver
Puesto que el ángulo entre el eje $x$ positivo y la recta tangente es $3\pi/4$, la pendiente de esa recta es $-1$, lo que significa que $y'(0)=1$; hemos de derivar la expresión de $y(x)$ e imponer que la derivada cumpla esa condición:
$$y'(x)=-C_1\,\mbox{sen}\, x+C_2\cos x+\frac{1}{2}\mbox{sen}\, x+\frac{x}{2}\cos x-x\cos x+\frac{x^2}{2}\mbox{sen}\, x$$
luego
$$y'(0)=C_2=-1$$
Por tanto, la solución buscada es
$$y(x)=\left(1-\frac{x^2}{2}\right)\cos x+\left(\frac{x}{2}-1\right)\,\mbox{sen}\, x$$
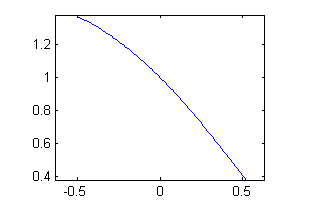
Para representarla en el ordenador con $x$ en $[-\pi/6,\pi/6]$, pondremos
>> x=linspace(-pi/6,pi/6); >> plot(x,(1-x.^2/2).*cos(x)+(x/2-1).*sin(x)) >> axis equalPedimos igual escala en los ejes para comprobar que efectivamente la pendiente de la gráfica en el punto $P(0,1)$ es $-1$:
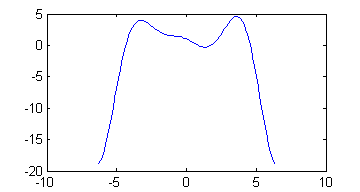
Las otras gráficas se obtienen con
>> x=linspace(-2*pi,2*pi); >> plot(x,(1-x.^2/2).*cos(x)+(x/2-1).*sin(x))
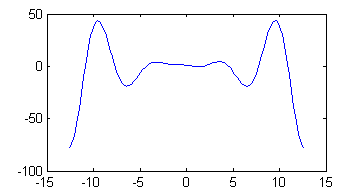
>> x=linspace(-4*pi,4*pi); >> plot(x,(1-x.^2/2).*cos(x)+(x/2-1).*sin(x))