Para encontrar esa relación entre las constantes $a$ y $b$ debemos comenzar ...

$$y=e^{mx} \ \ \Rightarrow\ \ y'=me^{mx} \ \ \Rightarrow\ \ y''=m^2e^{mx}$$ sustituyendo en la ecuación y sacando factor común $e^{mx}$, $$(2x-1)y''+(ax+b)y'-8y=0 \ \ \Rightarrow\ \ e^{mx}[(2x-1)m^2+(ax+b)m-8]=0$$ y puesto que $e^{mx}$ no se anula nunca, deberá ocurrir que $$(2x-1)m^2+(ax+b)m-8=0$$ De aquí se deduce que $$m=\frac{-(ax+b)\pm \sqrt{(ax+b)^2+32(2x-1)}}{2(2x-1)}$$

$$2m^2+am=0 \ \ \Rightarrow\ \ \ \ m=0 \ \ \mbox{o}\ \ m=-\frac{a}{2}$$ Pero puesto que $m=0$ no es solución de $-m^2+bm-8=0$, debe ocurrir que $m=-\frac{a}{2}$. Con esto, $$-m^2+bm-8=0\ \ \Rightarrow\ \ -\frac{a^2}{4}-\frac{ab}{2}-8=0 \ \ \Rightarrow\ \ a^2+2ab+32=0 \ \ \Rightarrow\ \ b=-\frac{32+a^2}{2a}$$ Conclusión: para que $e^{mx}$ sea solución de $(2x-1)y''+(ax+b)y'-8y=0$ debe ocurrir que $b=-\frac{32+a^2}{2a}$ y si se cumple eso, entonces $m=-\frac{a}{2}$. Continuar

Resolución del segundo apartado

En primer lugar, hemos de construir la ecuación correspondinte a ese valor de $a$: $$a=2\ \ \ \Rightarrow\ \ \ b=-\frac{32+4}{4}=-9 \ \ \mbox{y}\ \ m=-1$$ con lo cual sabemos que la ecuación es $$(2x-1)y''+(2x-9)y'-8y=0$$ y que una de sus soluciones es $y=e^{-x}$. Para hallar la solución general,

$$y_2=ve^{-x}\ \ \ \Rightarrow\ \ \ {y'}_2=e^{-x}(v'-v)\ \ \ \Rightarrow\ \ \ {y''}_2=e^{-x}(v''-2v'+v)$$ Sustituyendo en la ecuación $$e^{-x}[(2x-1)(v''-2v'+v)+(2x-9)(v'-v)-8v]=0$$ reordenando y agrupando en $v''$, $v'$ y $v$ y puesto que $e^{-x}$ no se anula, $$(2x-1)v''+(-4x+2+2x-9)v'+(2x-1-2x+9-8)v=0$$ o bien $$(2x-1)v''-(2x+7)v'=0$$ Esta es la ecuación que debe satisfacer $v'$. Se trata de una ecuación de variables separables en $v'$ y $x$. Resuélvela y pulsa en 'Continuar'. Continuar

$$(2x-1)v''-(2x+7)v'=0\ \ \ \Rightarrow\ \ \ \frac{v''}{v'}=\frac{2x+7}{2x-1}\ \ \mbox{o}\ \ x=\frac{1}{2}$$ $x=\frac{1}{2}$ es solución de $(2x-1)v''-(2x+7)v'=0$ pero no nos sirve en la búsqueda de $v(x)$; debemos seguir con la primera opción $$\frac{v''}{v'}=\frac{2x+7}{2x-1}\ \ \ \Rightarrow$$$$\Rightarrow\ \ \ \log|v'(x)|=\int\frac{2x+7}{2x-1}\, dx=\int\left(\frac{2x-1}{2x-1}+\frac{8}{2x-1}\right)\, dx=x+4\log|2x-1|+C \ \ \ \Rightarrow$$ $$\Rightarrow\ \ \ v'(x)=e^{x+4\log|2x-1|+C}=ke^x(2x-1)^4$$ Podemos tomar $k=1$ porque sólo necesitamos una función $v'(x)$ de esa familia, no la solución general. Ahora que tenemos $v'(x)$ obtendremos $v(x)$ por integración directa. Podemos utilizar Matlab u otro programa de cálculo simbólico o bien hacerla a mano. En este último caso recurriríamos a integración por partes para encontrar iterativamente la primitiva. Si recurrimos a Matlab, ejecutaremos

>> syms x
>> int(exp(x)*(2*x-1)^4)
 

obteniendo

exp(x)*(16*x^4 - 96*x^3 + 312*x^2 - 632*x + 633)

Con esto podemos concluir que $$y_2(x)=v(x)e^{-x}=16x^4 - 96x^3 + 312x^2 - 632x + 633$$ y que la solución general de la ecuación $$(2x-1)y''+(2x-9)y'-8y=0$$ es $$y(x)=C_1e^{-x}+C_2(16x^4 - 96x^3 + 312x^2 - 632x + 633)$$ Continuar

Resolución del tercer apartado

Antes de escribir las líneas de código debemos expresar los coeficientes $C_1$ y $C_2$ presentes en la solución general en función del punto de paso $(0,y_0)$ y la pendiente en ese punto. Encuentra esas expresiones y pulsa en 'Continuar'. Continuar

$$y(x)=C_1e^{-x}+C_2(16x^4 - 96x^3 + 312x^2 - 632x + 633)\ \ \Rightarrow\ \ y(0)=C_1+633C_2$$ Derivando y sustituyendo en $x=0$, $$y'(x)=-C_1e^{-x}+C_2(64x^3 -288x^2 +624x - 632)\ \ \Rightarrow\ \ y'(0)=-C_1-632C_2$$ Tenemos así un sistema de dos ecuaciones en las incógnitas $C_1$ y $C_2$: $$y(0)=C_1+633C_2\ \ \ ,\ \ \ y'(0)=-C_1-632C_2$$ Sumando estas ecuaciones llegamos a $$C_2=y(0)+y'(0)$$ y despejando $C_1$ en la primera tendremos $C_1=y(0)-633(y(0)+y'(0))$ o bien $$C_1=-632y(0)-633y'(0)$$ Ahora ya podemos escribir la solución general en función de $y(0)$, que es la ordenada del punto de corte de la curva solución con el eje $0Y$, y la pendiente $y'(0)$ en ese punto: $$y(x)=-[632y(0)+633y'(0)]e^{-x}+[y(0)+y'(0)](16x^4 - 96x^3 + 312x^2 - 632x + 633)$$ y con ella construir la función Matlab descrita en el enunciado. En cada fase que se plantea a continuación piensa cómo hacerlo y pulsa en 'Continuar':

• Escribe la cabecera de la función, el nombre de la función será dibujasol y el de las tres variables de entrada será a, ordenadas y pendientes:

Continuar

function dibujasol(a,ordenadas,pendientes)

• Genera un vector x con valores entre $-a$ y $a$

Continuar

x=linspace(-a,a,50);

• Guarda en una variable llamada numo el número de ordenadas y en nump el número de pendientes:

Continuar

numo=length(ordenadas); nump=length(pendientes);

• Supondremos que en el fichero que contenga al código de esta función se definirá a continuación de ésta una función auxiliar, llamada dibujasolaux, que tiene como variables de entrada un vector de abscisas, una ordenada y una pendiente y dibuja la curva solución que pasa por el punto del eje $0Y$ con esa ordenada y esa pendiente. Escribe las líneas de código de dos ciclos for enlazados que vaya leyendo las componentes de ordenadas y las de pendientes y dibuje las correspondientes soluciones:

Continuar

for n=1:numo
    for m=1:nump
        dibujasolaux(x,ordenadas(n),pendientes(m))
        hold on
    end
end

• Añade una malla a la figura, ciérrala y termina la función:

Continuar

grid on
hold off
end

• Tenemos ahora que escribir la función auxiliar. Escribe el código restante si la cabecera es:

 function dibujasolaux(x,y0,p0) 

Continuar

y=-(632*y0+633*p0)*exp(-x)+(y0+p0)*(16*x.^4-96*x.^3+312*x.^2-632*x+633);
plot(x,y)
end

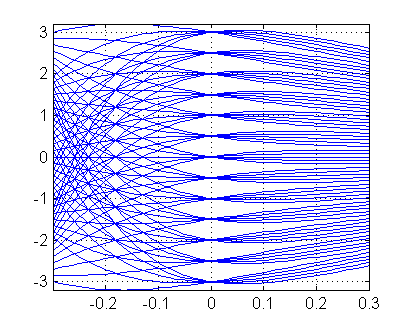
• Con esto ya está terminado el código. Escribe ahora la línea que ejecutas para dibujar en el intervalo $[-a,a]$ las soluciones que pasan por los puntos $(0,-3)$, $(0,-2.5)$, $(0,-2)$, $(0,-1.5)$, $(0,-1)$, $(0,-0.5)$, $(0,0)$, $(0,0.5)$, $(0,1)$, $(0,1.5)$, $(0,2)$, $(0,2.5)$ y $(0,3)$ y tienen pendientes $-2$, $-1$, $0$, $1$ y $2$:

Continuar

dibujasol(.3,-3:.5:3,-2:2)

La figura resultante es