Enunciado
A un problema de valores en la frontera del tipo
$$y''(x)-\sqrt{12} y'(x)+\lambda y(x)=0 \hspace{.5cm} ,\hspace{.5cm} y(0)=0
\hspace{.5cm} ,\hspace{.5cm} y(\pi)=0$$
se le denomina problema de valores propios. Puesto que la ecuación es homogénea, la solución $y(x)=0$ (solución trivial) es válida para cualquier valor del parámetro $\lambda$, pero no es interesante. Lo que interesa son precisamente las soluciones no triviales.
- Analiza para qué valores de $\lambda$ el problema anterior tiene soluciones no triviales y halla esas soluciones.
- Genera una función para el ordenador que represente una muestra de soluciones para un valor del parámetro.
Resolución del primer apartado
Paso 1
El parámetro $\lambda$ puede en principio tomar cualquier valor real, pero no depende de la variable $x$, así que la ecuación es una ecuación lineal de coeficientes constantes y homogénea; procederemos escribiendo su ecuación característica y las raíces de ésta. Hazlo tú y pulsa en 'Ver'.
Ver
La ecuación característica es $$r^2-\sqrt{12} r+\lambda=0$$ de raíces
$$r=\frac{\sqrt{12}\pm\sqrt{12-4\lambda}}{2}=\frac{2\sqrt{3}\pm 2\sqrt{3-\lambda}}{2}=
\sqrt{3}\pm \sqrt{3-\lambda}$$
Paso 2
La solución general es por tanto
$$y(x)=e^{\sqrt{3}x}(A\cos \sqrt{3-\lambda}x +B\,\mbox{sen}\, \sqrt{3-\lambda}x)$$
$$y(x)=e^{\sqrt{3}x}(Ae^{\sqrt{3-\lambda}x} +Be^{-\sqrt{3-\lambda}x})$$
$$y(x)=e^{\sqrt{3}x}(A+Bx)$$
Ninguna de las presentadas es la solución general para cualquier $\lambda$.
Las raíces de la ecuación característica serán complejas si $3-\lambda< 0$; pero entonces, la parte imaginaria de esas raíces no es $\sqrt{3-\lambda}$.
Esa forma para la solución general sería correcta sólo en el caso en que $3-\lambda>0$
Esa forma para la solución general sería correcta sólo en el caso en que $3-\lambda=0$
En efecto, la forma de la solución general depende del signo de $3-\lambda$. Debemos pues estudiar separadamente los tres casos que se producen según el signo de $3-\lambda$.
Caso 1
$3-\lambda>0$, es decir, si $\lambda<3$
Paso 1 para el Caso 1
Para simplificar la escritura, podemos llamar $\alpha^2=3-\lambda$, siendo $\alpha>0$. Las dos raíces reales y distintas de la ecuación característica son $$r=\sqrt{3}\pm\alpha$$Paso 2 para el Caso 1
La solución general es $$y(x)=e^{\sqrt{3}x}(Ae^{\alpha x} +Be^{-\alpha x})$$Paso 3 para el Caso 1
Imponemos las condiciones de contorno. Realiza tú este paso y pulsa en 'Ver'.
Ver
$$y(0)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(0)=A+B=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} A=-B$$
$$y(\pi)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(\pi)=Ae^{\sqrt{3}\pi}(e^{\alpha \pi} -e^{-\alpha \pi})=0$$
Puesto que $\alpha$ no es cero, no puede ser que $e^{\alpha \pi} -e^{-\alpha \pi}$ sea cero, así que lo que debe anularse es el coeficiente $A$. Por tanto, la única solución posible en este caso es $y(x)=0$; para cualquier $\lambda$ de valor inferior a $3$, la única solución del problema de valores en la frontera es la trivial.
Caso 2
$3-\lambda=0$, es decir, si $\lambda=3$
Paso 1 para el Caso 2
En este caso la única solución de la ecuación caracteristica es $$r=\sqrt{3}$$Paso 2 para el Caso 2
La solución general es $$y(x)=e^{\sqrt{3}x}(A+Bx)$$Paso 3 para el Caso 2
Imponemos las condiciones de contorno. Realiza tú este paso y pulsa en 'Ver'.
Ver
$$y(0)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(0)=A=0$$
$$y(\pi)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(\pi)=e^{\sqrt{3}\pi}B\pi=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} B=0$$
Concluimos que la única solución posible también en este caso es $y(x)=0$.
Caso 3
$3-\lambda<0$, es decir, si $\lambda>3$
Paso 1 para el Caso 3
Igual que el caso 1, simplificamos la notación introduciendo el parámetro $\alpha$ que cumple $-\alpha^2=3-\lambda$, $\alpha>0$. Las raíces de la ecuación caracteristica son entonces $$r=\sqrt{3}\pm\sqrt{-\alpha^2}$$ Puesto que ese radicando es negativo, las escribimos como $$r=\sqrt{3}\pm i\sqrt{\alpha^2}=\sqrt{3}\pm i\alpha$$Paso 2 para el Caso 3
La solución general es ... escríbela y pulsa en 'Ver'
Ver
$$y(x)=e^{\sqrt{3}x}(A\cos \alpha x +B\,\mbox{sen}\,\alpha x)$$
Paso 3 para el Caso 3
Imponemos las condiciones de contorno: $$y(0)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(0)=A=0$$ $$y(\pi)=0 \hspace{.5cm} \Rightarrow \hspace{.5cm} y(\pi)=e^{\sqrt{3}\pi}B\,\mbox{sen}\,\alpha\pi=0$$ Esto significa que
Tanto $A$ como $B$ deben ser nulas.
Ninguna es correcta.
El único valor posible de $\alpha$ (para conseguir solución $y(x)$ no trivial), es $\alpha=0$.
$\mbox{sen}\,\alpha\pi$ debe ser nulo.
La expresión $e^{\sqrt{3}\pi}B\,\mbox{sen}\,\alpha\pi=0$ puede ser cierta sin que $B$ sea cero.
Sí hay una correcta.
Es cierto que la expresión $e^{\sqrt{3}\pi}B\,\mbox{sen}\,\alpha\pi=0$ es cumple si $\alpha=0$, pero también lo cumple con otros valores de $\alpha$
En efecto, puesto que estamos buscando soluciones no triviales, debemos intentar que $B$ no sea cero. Para que cumpla la expresión $e^{\sqrt{3}\pi}B\,\mbox{sen}\,\alpha\pi=0$, debemos imponer que
$$\mbox{sen}\,\alpha\pi=0$$
Esto ocurriría para cualquier valor $\alpha$ entero. Puesto que pusimos como condición para $\alpha$ que fuera positivo, eso nos quita los negativos y el cero, así que tendremos un valor posible de $\alpha$ para cada número natural: $$\alpha_n=n \hspace{.5cm} ,\hspace{.5cm} n\in{\bf N}$$
que nos genera por tanto una sucesión de valores posibles del parámetro $\lambda$ (recuerda que
$-\alpha^2=3-\lambda$):
$$\lambda_n=3+n^2 \hspace{.5cm} ,\hspace{.5cm} n\in{\bf N}$$
Observa que de imponer las dos condiciones en la frontera no se obtiene ninguna restricción para el valor del coeficiente $B$, de manera que cualquier función de la forma
$$y(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,n x$$ es solución del problema correspondiente a $\lambda_n=3+n^2$. Esto no es extraño, pues tratándose de una ecuación homogénea acompañada de condiciones también homogéneas, los múltiplos de una solución también deben ser soluciones.
Conclusión
A cada uno de los valores de $\lambda$ de la forma $\lambda_n=3+n^2$ con $n$ natural le corresponde una ecuación diferencial distinta y por tanto una familia de soluciones no triviales propia. Por ejemplo, para $n=1$ tendremos que $\lambda_1=4$, la ecuación es $$y''(x)-\sqrt{12} y'(x)+4 y(x)=0$$ Las soluciones de esta ecuación cumpliendo que $y(0)=0$ y que $y(\pi)=0$ son $$y_1(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,x$$ Para $n=2$, la ecuación es $$y''(x)-\sqrt{12} y'(x)+7 y(x)=0$$ y sus soluciones con $y(0)=0$ e $y(\pi)=0$ son $$y_2(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,2x$$ En general, cada problema de la forma $$y''_n(x)-\sqrt{12} y'_n(x)+(3+n^2) y_n(x)=0 \hspace{.5cm} ,\hspace{.5cm} y(0)=0 \hspace{.5cm} ,\hspace{.5cm} y(\pi)=0$$ con $n$ un número natural, tiene como conjunto de soluciones $$y_n(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,nx$$Resolución del segundo apartado
El objetivo de este apartado es generar una función para el ordenador que tome como variable de entrada un valor natural, $n$, y represente una muestra de las soluciones del correspondiente problema: $$y''_n(x)-\sqrt{12} y'_n(x)+(3+n^2) y_n(x)=0 \hspace{.5cm} ,\hspace{.5cm} y(0)=0 \hspace{.5cm} ,\hspace{.5cm} y(\pi)=0$$ que sabemos que son $$y_n(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,nx$$ Es decir, debemos dar un conjunto de valores al parámetro $B$ y dibujar las funciones en el intervalo $[0,\pi]$. Si escribimos en el fichero 'curvassol.m' la siguiente definición
function curvassol(n)
%%% muestra de la familia de soluciones de y''-sqrt(12)y'+(3+n^2)y=0, y(0)=0,y(pi)=0
b=.4:.4:2;
x=linspace(0,pi);
[X,B]=meshgrid(x,b);
Y=B.*exp(sqrt(3)*X).*sin(n*X);
plot(x,Y)
xlabel('x');ylabel('y')
end
y ejecutamos en la ventana de comandos
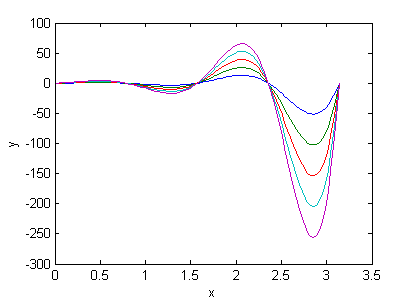
>> curvassol(1)obtendremos una figura con las cinco soluciones $$y_1(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,x$$ correspondientes a $B=0.4$, $B=0.8$, $B=1.2$, $B=1.6$ y $B=2$.
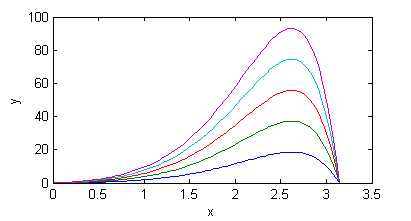
>> curvassol(2)tendremos las cinco soluciones $$y_2(x)=Be^{\sqrt{3}x}\,\mbox{sen}\,2x$$ para los mismos valores de $B$:
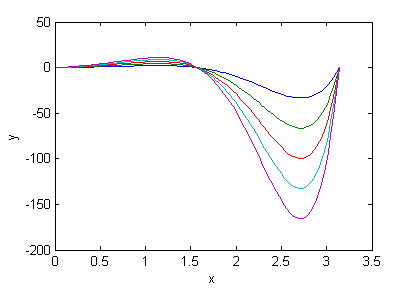
>> curvassol(3)
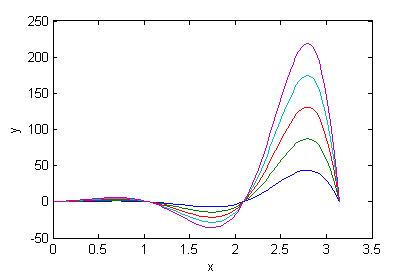
>> curvassol(4)