Enunciado
Considera la ecuación lineal de coeficientes constantes homogénea siguiente
$$y''+3y'+qy=0$$
- Escoge un valor de $q$ para el cual la solución general de esa ecuación sea de la forma
$$y(x)=C_1e^{r_1x}+C_2e^{r_2x}\hspace{.7cm}\mbox{con}\hspace{.7cm} C_1\ ,\ C_2 \in {\bf R}$$
siendo $r_1$ y $r_2$ dos números reales diferentes.
- Fija un punto de paso y escribe las líneas para el ordenador con las que dibujas seis de esas soluciones que pasen por el punto fijado.
- Fija una pendiente en $x=0$ y escribe las órdenes con las que dibujas seis soluciones, diferentes a las del apartado anterior, que tengan esa pendiente en $x=0$.
- Escoge un valor de $q$ para el cual la solución general de la ecuación sea de la forma
$$y(x)=e^{ax}(C_1\cos bx+C_2\,\mbox{sen}\, bx)\hspace{.7cm}\mbox{con}\hspace{.7cm} C_1\ ,\ C_2 \in {\bf R}$$
siendo $a$ y $b$ números reales.
- Fija unas condiciones iniciales y encuentra la solución particular correspondiente. Represéntala en un intervalo apropiado.
- Considera que la ecuación fuera válida en el intervalo $[0,\frac{\pi}{\sqrt{4q-p}}]$ (siendo $q$ el valor escogido por tí). Fija unas condiciones de frontera y encuentra la solución correspondiente. Represéntala en el intervalo $[0,\frac{\pi}{\sqrt{4q-p}}]$.
- Fija un punto de paso y escribe las líneas para el ordenador con las que dibujas seis de esas soluciones que pasen por el punto fijado.
- Fija una pendiente en $x=0$ y escribe las órdenes con las que dibujas seis soluciones, diferentes a las del apartado anterior, que tengan esa pendiente en $x=0$.
- Fija unas condiciones iniciales y encuentra la solución particular correspondiente. Represéntala en un intervalo apropiado.
- Considera que la ecuación fuera válida en el intervalo $[0,\frac{\pi}{\sqrt{4q-p}}]$ (siendo $q$ el valor escogido por tí). Fija unas condiciones de frontera y encuentra la solución correspondiente. Represéntala en el intervalo $[0,\frac{\pi}{\sqrt{4q-p}}]$.
Resolución del primer apartado
Para resolver este apartado nos basamos en la construcción de la solución general de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes. Para la ecuación del enunciado, la ecuación característica y sus raíces son ... búscalas y pulsa en 'Ver' cuando las tengas.
Ver
La ecuación característica es $$r^2+3r+q=0$$ cuyas raíces son
$$r=\frac{-3\pm \sqrt{9-4q}}{2}$$
En este apartado debemos elegir un valor de $q$ que haga que $9-4q$ sea positivo, para que estas raíces sean reales y distintas. Por tanto podemos elegir cualquier valor de $q$ tal que $$q<\frac{9}{4}$$
Por ejemplo, con $q=2$ las raíces son $r_1=-2$ y $r_2=-1$, luego la solución general de la ecuación
$$y''+3y'+2y=0$$ es $$y(x)=C_1e^{-2x}+C_2e^{-x} \hspace{.5cm},\hspace{.5cm}C_1\, ,\ C_2 \in {\bf{R}}$$
Apartado 1a)
Fijamos como punto de paso $P(0,1)$: imponemos que $y(0)=1$, con lo cual
Sólo podría ser $q=0$, pues $y'$ e $y''$ serían cero.
$C_1+C_2=1$
$y'$ e $y''$ no son cero, pues no se deriva lo que vale $y$ en un punto. Trabajamos sobre la expresión de la solución general.
En efecto, $C_1$ y $C_2$ están relacionadas según $C_1+C_2=1$. Podemos despejar una en función de la otra y sustituir en la solución general. Por ejemplo, con $C_2=1-C_1$, obtenemos que la soluciones que pasan por el punto $P(0,1)$ son las de la familia uniparamétrica
$$y(x)=C_1e^{-2x}+(1-C_1)e^{-x} \hspace{.5cm},\hspace{.5cm}C_1 \in {\bf{R}}$$
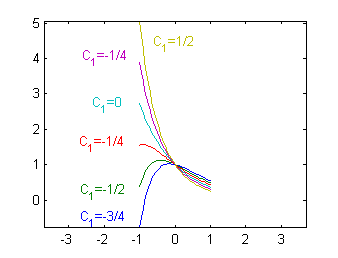
Debemos ahora dibujar seis de esas curvas en el ordenador. Tomaremos los siguientes valores para $C_1$:
$$\frac{-3}{4},\ \frac{-1}{2},\ \frac{-1}{4},\ 0 ,\ \frac{1}{4},\ \frac{1}{2}$$ para dibujar las correspondientes curvas en el intervalo $[-1,1]$.
Una opción es utilizar un ciclo 'for' que las vaya dibujando.
c=(-3:2)/4;
x=-1:.05:1;
for k=1:6
plot(x,c(k)*exp(-2*x)+(1-c(k))*exp(-x))
hold on
end
hold off
axis equal
Con este código obtendremos la figura:
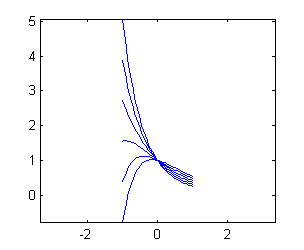
c=(-3:2)/4; x=-1:.05:1; [X,C]=meshgrid(x,c); Y=C.*exp(-2*X)+(1-C).*exp(-X); plot(x,Y) axis equal

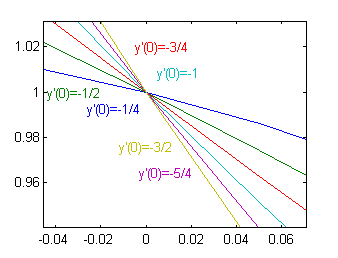
Hemos elegido varios valores del parámetro sin interesarnos por su relación con las pendientes de las curvas resultantes en el punto común, $P(0,1)$. Podemos analizar cúales son esas pendientes, calculando la derivada de esas funciones en $x=0$:
$$y(x)=C_1e^{-2x}+(1-C_1)e^{-x} \hspace{.7cm}\Rightarrow\hspace{.7cm} y'(x)=-2C_1e^{-2x}-(1-C_1)e^{-x}
\hspace{.7cm}\Rightarrow\hspace{.7cm} y'(0)=-C_1-1$$
Así que las pendientes en $P(0,1)$ de las curvas que hemos dibujado son
$$\frac{-1}{4},\ \frac{-1}{2},\ \frac{-3}{4},\ -1 ,\ \frac{-5}{4},\ \frac{-3}{2}$$
que podemos observar si aumentamos el zoom cerca del punto $P(0,1)$:
Apartado 1b)
De la solución general $$y(x)=C_1e^{-2x}+C_2e^{-x} \hspace{.5cm},\hspace{.5cm}C_1\, ,\ C_2 \in {\bf{R}}$$ debemos extraer las curvas que tengan una pendiente fijada por nosotros en el punto correspondiente a $x=0$. Si por ejemplo fijamos esa pendiente para que sea 1, las curvas serán... búscalas y pulsa en 'Ver'.
Ver
$$y'(x)=-2C_1e^{-2x}-C_2e^{-x}\hspace{.7cm}\Rightarrow\hspace{.7cm} y'(0)=-2C_1-C_2=1$$
Podemos tomar $C_2=-2C_1-1$, con lo cual la familia uniparamétrica de soluciones que tienen pendiente 1 cuando $x=0$ es
$$y(x)=C_1e^{-2x}-(2C_1+1)e^{-x}\ ,\ C_1\in{\bf R}$$
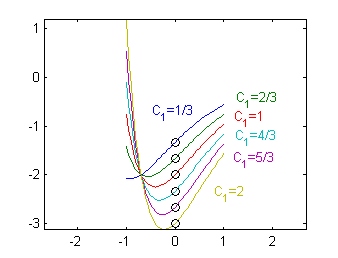
Cada una de estas curvas pasa por el punto $P(0,-C_1-1)$.
Dibujamos las corrrespondientes a $C_1=n/3$ para $n=1$ a $n=6$ y marcamos el punto de corte con el eje $x=0$:
c=(1:6)/3; x=-1:.05:1; [X,C]=meshgrid(x,c); Y=C.*exp(-2*X)-(2*C+1).*exp(-X); plot(x,Y) hold on plot(zeros(1,6),-c-1,'ok') axis equal hold off
Resolución del segundo apartado
Recordamos de nuevo la construcción de la solución general de una e.d.o. lineal de segundo orden homogénea de coeficientes constantes. Debemos ahora caracterizar los valores de $q$ para los cuales las raíces de la ecuación característica sean complejas, es decir, $$9-4q<0$$ o bien $$q>\frac{9}{4}$$ Por ejemplo, con $q=3$, la ecuación diferencial es $$y''+3y'+3y=0$$ y su solución general es $$y(x)=e^{-3x/2}\left(C_1\cos \frac{\sqrt{3}}{2}x+C_2 \,\mbox{sen}\,\frac{\sqrt{3}}{2}x \right) \hspace{.5cm},\hspace{.5cm}C_1\, ,\ C_2 \in {\bf{R}}$$Apartado 2a)
Hemos de imponer ahora unas condiciones iniciales, como por ejemplo (selecciona)
$y(0)=0$, $y'(\pi)=1$
$y(0)=1$, $y(\pi/\sqrt{3})=-1$
$y(0)=1$, $y'(0)=-1$
Eso no son condiciones iniciales.
Eso no son condiciones iniciales.
Estas sí son condiciones iniciales, pues dan el valor de la función y el de su derivada para un mismo valor de $x$, en este caso $x=0$. Encuentra para estas condiciones los valores correspondientes de los parámetros $C_1$ y $C_2$ de la solución
$$y(x)=e^{-3x/2}\left(C_1\cos \frac{\sqrt{3}}{2}x+C_2 \,\mbox{sen}\,\frac{\sqrt{3}}{2}x \right)$$
y pulsa en 'Continuar' cuando termines.
Imponiendo que $y(0)=1$ obtendremos que $C_1=1$, y la condición $y'(0)=-1$ implica que $-3C_1+\sqrt{3}C_2=-2$ de donde $C_2=1/\sqrt{3}$. Así que la solución particular, que pasa por el punto $P(0,1)$ con pendiente $-1$ es $$y(x)=e^{-3x/2}\left(\cos \frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{3} \,\mbox{sen}\,\frac{\sqrt{3}}{2}x \right)$$
que representamos con el código
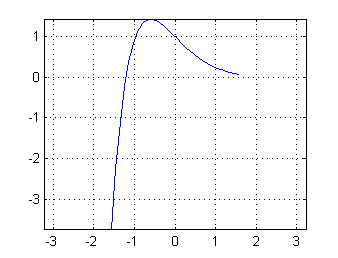
x=linspace(-pi/2,pi/2,30); r=sqrt(3); plot(x,exp(-3*x/2).*(cos(r*x/2)+r*sin(r*x/2)/3)) axis equal grid on

Apartado 2b)
Puesto que tomamos $q=3$, el intervalo en que se considera la ecuación $y''+3y'+3y=0$ es $[0,\pi/\sqrt{3}]$. Unas condiciones de frontera podrían ser
$y(0)=-1$, $y'(\pi/\sqrt{3})=1$
$y'(0)=1$, $y(\pi/\sqrt{3})=-1$
$y(0)=1$, $y(\pi/\sqrt{3})=-1$
Eso no son condiciones de frontera.
Eso no son condiciones de frontera.
Estas sí son condiciones de frontera, pues dan el valor de la función en los extremos del intervalo. Encuentra para estas condiciones los valores correspondientes de los parámetros $C_1$ y $C_2$ de la solución
$$y(x)=e^{-3x/2}\left(C_1\cos \frac{\sqrt{3}}{2}x+C_2 \,\mbox{sen}\,\frac{\sqrt{3}}{2}x \right)$$ y pulsa en 'Continuar' cuando termines.
Imponiendo que $y(0)=1$ obtendremos que $C_1=1$, y la condición $y(\pi/\sqrt{3})=-1$ implica que
$$e^{-\sqrt{3}\pi/2}C_2=-1$$ de donde obtenemos $C_2$. Así que la solución particular, que pasa por los puntos $P(0,1)$ y $Q(\pi/\sqrt{3},-1)$ es
$$y(x)=e^{-3x/2}\left(\cos \frac{\sqrt{3}}{2}x-e^{\sqrt{3}\pi/2}\,\mbox{sen}\,\frac{\sqrt{3}}{2}x \right)$$
que representamos con el código
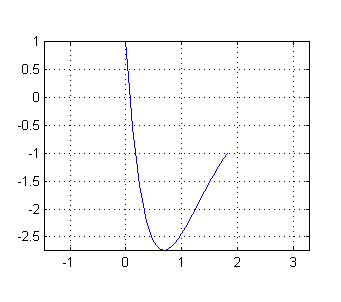
r=sqrt(3); x=linspace(0,pi/r,30); plot(x,exp(-3*x/2).*(cos(r*x/2)-exp(r*pi/2)*sin(r*x/2))) axis equal grid on
