Enunciado
Un depósito contiene inicialmente 100 gramos de sal disueltos en 6 litros de disolución. Durante los primeros 5 minutos se vierte disolución a razón de 5 dl/min. con 12 gr/l. Tras esos 5 minutos se abre un orificio de salida (el flujo de entrada se mantiene igual y con la misma concentración).
- CASO 1: Supón que el flujo de salida es 5 dl/min. Calcula en ese supuesto la cantidad de sal en el depósito cuando hayan transcurrido 5 minutos más.
- CASO 2: Supón que el flujo de salida es 3 dl/min. Calcula en ese supuesto la cantidad de sal en el depósito cuando se empiece a desbordar, sabiendo que su capacidad total es 10 litros.
Resolución
Este es un problema de disolución en un depósito que debe estudiarse en dos fases: en la primera fase (primeros 5 minutos) entra disolución pero no sale; en la segunda fase (5 minutos siguientes) entra y sale disolución. Podemos esquematizar esta información en las siguientes tablas:
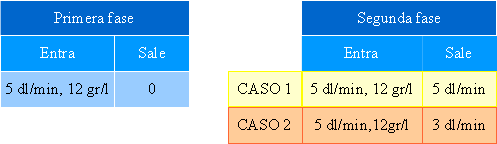
Estudio de la primera fase
La tasa de entrada de disolución, en litros por minutos, es de $1/2$; la concentración de sal en este flujo de entrada es de 12 gramos en cada litro. Eso significa que cada minuto:- el volumen de disolución en el depósito aumenta $1/2$ litro
- la cantidad de sal presente en el depósito aumenta en 6 gramos
Ver
Cuando hayan transcurrido 5 minutos, el volumen será $$V_1=6+\frac{5}{2}=\frac{17}{2}$$
y la cantidad de sal será $$S_1=100+6\cdot 5=130$$
Estudio de la segunda fase para el CASO 1
El balance de masa en el depósito es $$\mbox{Tasa de cambio}=\mbox{Tasa de entrada}-\mbox{Tasa de salida}$$ Si llamamos- $V$ al volumen de disolución en el depósito,
- $S$ a la cantidad de sal en el depósito,
$\frac{dS}{dt}=6-\frac{130}{17}$
ya que al comienzo de esta fase, $S=S_1=130$ y $V=V_1=17/2$.
$\frac{dS}{dt}=6-\frac{S}{12+t}$
ya que $V=6+t/2$ (al entrar $1/2$ litro por minuto)
$\frac{dS}{dt}=6-\frac{S}{12}$
porque al entrar el mismo volumen que salir, $V=6$.
Ninguna de las ecuaciones es correcta.
$\frac{dS}{dt}=6-\frac{S}{17}$
debido a que entra el mismo volumen que sale, $V=V_1=17/2$
No es correcto. $S$ es variable con el tiempo: $S=130$ sólo es para $t=5$.
No es correcto. $V=6+t/2$ en la primera fase (primeros 5 minutos)
No es correcto. Es cierto que el volumen es constante, pero no es igual a 6 litros.
Sí hay una correcta.
En efecto, esa es la ecuación, que irá acompañada de la condición inicial $S(5)=S_1=130$. Encuentra la solución de ese problema de valor inicial y pulsa en 'Continuar'.
Se trata de una ecuación de variables separables:
$$\frac{dS}{102-S}=\frac{dt}{17}\hspace{1cm}\Rightarrow \hspace{1cm} -\log|102-S|=\frac{t}{17}+C_1$$
o bien $$S(t)=102+Ce^{-t/17}$$
Imponiendo que $S(5)=130$,
$$S(5)=102+Ce^{-5/17}=130 \hspace{1cm}\Rightarrow \hspace{1cm} C=28e^{5/17}$$
obtenemos la particular $$S(t)=102+28e^{(5-t)/17}$$
Por tanto, cuando hayan transcurrido 5 minutos más, la cantidad de sal disuelta en el depósito será
$$S(10)=102+28e^{-5/17}\approx 122.86$$
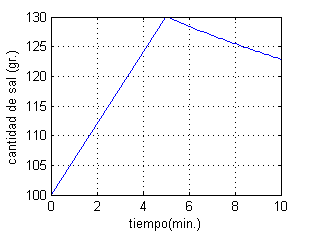
Prepara el código para dibujar la gráfica de la función cantidad de sal respecto del tiempo para $t$ desde $t=0$ hasta $t=10$ y pulsa en 'Ver'.
Ver
Durante los primeros 5 minutos, la función cantidad es una recta, luego no le daremos más que el primer punto ($t=0$, $S=100$) y el último (que es el primero del segundo tramo):
%caso 1
t=5:.1:10;
plot([0 t],[100 102+28*exp((5-t)/17)] )
grid on
xlabel('tiempo (min.)');ylabel('cantidad de sal (gr.)')
Estudio de la segunda fase para el CASO 2
Igual que antes, el balance de masa en el depósito es $$\mbox{Tasa de cambio}=\mbox{Tasa de entrada}-\mbox{Tasa de salida}$$ Como en el caso anterior, dejaremos el origen de tiempos al comienzo de la primera fase, considerando por tanto que el comienzo de esta segunda fase es $t=5$. La diferencia con el caso 1 estriba en el volumen, ya que ahora no son iguales el de entrada y el de salida. El flujo de entrada es $1/2$ l/min y el de salida es $3/10$ l/min, siendo el volumen inicial $V_1=17/2$; por tanto el volumen será la función ...
$V(t)=\frac{17}{2}+\left(\frac{1}{2}-\frac{3}{10}\right)t$
$V(t)=\frac{17}{2}+\left(\frac{3}{10}-\frac{1}{2}\right)t$
$V(t)=\frac{17}{2}\left(\frac{1}{2}-\frac{3}{10}\right)t$
Ninguna de las propuestas es correcta.
Cuidado con el origen de tiempos. Con esa expresión para el volumen, para $t=5$ (origen en esta fase), el volumen sería $19/2$ y no $17/2$.
No es correcta por dos razones.
Estás multiplicando el volumen inicial por la variación del volumen. No es correcto.
En efecto, ninguna de las expresiones es correcta. Lo correcto es
$$V(t)=\frac{17}{2}+\left(\frac{1}{2}-\frac{3}{10}\right)(t-5)=
\frac{17}{2}+\frac{1}{5}(t-5)=\frac{15}{2}+\frac{t}{5}$$
pues es en $t=5$ cuando se abre el orificio de salida.
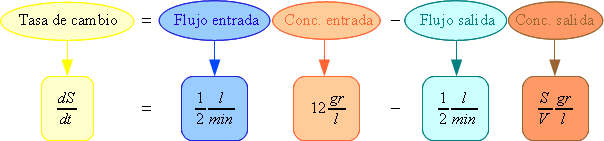
Escribe ahora la ecuación diferencial para $S$ siguiendo el esquema
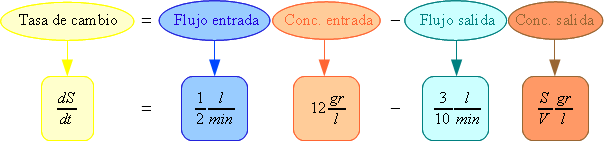
La ecuación es
$$\frac{dS}{dt}=6-3\frac{S(t)}{75+2t}$$
que es lineal:
$$\frac{dS}{dt}+\frac{3}{75+2t}S(t)=6$$
Podemos resolverla por tanto mediante la
aplicación del factor integrante $$\mu(t)=e^{\int p(t)\, dt}\hspace{1cm} \mbox{siendo} \hspace{1cm} p(t)=\frac{3}{75+2t}$$
Encuentra con este método la solución general y luego pulsa en 'Ver'.
Ver
La solución general resulta $$S(t)=12\left(\frac{15}{2}+\frac{t}{5}\right)+C\left(\frac{15}{2}+\frac{t}{5}\right)^{-3/2}$$
Imponiendo la condición $S(5)=130$ obtenemos la particular
$$S(t)=12\left(\frac{15}{2}+\frac{t}{5}\right)+28\left(\frac{17}{15+2t/5}\right)^{3/2}$$
Ahora debemos averiguar el valor de esta función cuando el depósito empieza a desbordar. Para ello debemos primero determinar cuál es el valor del tiempo en que el volumen alcanza el máximo (10 litros) y después evaluar $S$ en ese valor del tiempo. Haz las dos operaciones y pulsa en 'Continuar'.
Si $t_f$ es el momento en que el volumen llega al máximo,
$$V(t_f)=\frac{15}{2}+\frac{t_f}{5}=10 \hspace{1cm}\Rightarrow \hspace{1cm} t_f=\frac{25}{2}$$
La cantidad de sal en ese momento es
$$S\left(\frac{25}{2}\right)=120+28\left(\frac{17}{20}\right)^{3/2}\approx 141.94$$
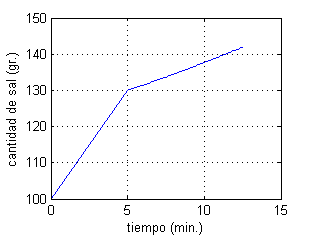
Aunque no se pida en el enunciado, podemos dibujar la gráfica de la cantidad de sal para $t$ desde $t=0$ hasta $t=t_f$:
tf=25/2;
t=5:.1:tf;
% caso 2
plot([0 t],[100 12*(15/2+t/5)+28*(17./(15+2*t/5)).^(3/2)] )
grid on
xlabel('tiempo (min.)');ylabel('cantidad de sal (gr.)')