Enunciado
Dada la ecuación diferencial de primer orden $$\left(4x^2-6xy+\frac{y^2}{x}\right)\, dx=2(x^2-y)\, dy$$
- Analiza si es exacta.
- Analiza si admite un factor integrante que sea sólo función de $x$ y en ese caso encuéntralo.
- Resuelve la ecuación.
- Dibuja una muestra de soluciones utilizando el comando 'contour'.
- Halla y representa la solución que pasa por el punto $(1,2)$
- Halla y representa la solución que pasa por el punto $(2,2)$
Resolución del primer apartado
Escribe la ecuación en la forma $M(x,y)\, dx+N(x,y)\, dy=0$, para identificar cuáles son en este caso las funciones $M(x,y)$ y $N(x,y)$ y aplicar el test de exactitud . Pulsa en 'Ver' cuando lo hayas comprobado.
Ver
Escrita de la forma
$$\left(4x^2-6xy+\frac{y^2}{x}\right)\, dx+2(y-x^2)\, dy=0$$
vemos que $$M(x,y)=4x^2-6xy+\frac{y^2}{x} \hspace{1cm},\hspace{1cm} N(x,y)=2(y-x^2)$$
que evidentemente admiten derivadas parciales continuas en $x\neq 0$, luego podemos aplicar el test de exactitud en esa región.
Derivamos $M$ respecto de $y$ y $N$ respecto de $x$,
$$M'_y(x,y)=-6x+2\frac{y}{x} \hspace{1cm},\hspace{1cm} N'_x(x,y)=-4x$$
dado que estas derivadas no son iguales, la ecuación no es exacta.
Resolución del segundo apartado
Paso 1
Si la ecuación admite un factor integrante de la forma $\mu=\mu(x)$, éste de ser tal que $$\mu(x)M(x,y)\, dx+\mu(x)N(x,y)\, dy=0$$ sea exacta. Debemos por tanto imponer que esta última ecuación cumpla el test de exactitud, para lo cual calculamos las correspondientes derivadas, que en este caso son ...
$$\frac{\partial}{\partial y}(\mu(x) M(x,y))=\frac{\partial \mu(x)}{\partial y} M(x,y)+\mu(x) \frac{\partial M}{\partial y}(x,y)$$
$$\frac{\partial}{\partial x}(\mu(x) N(x,y))=\frac{\partial \mu(x)}{\partial x} N(x,y)+\mu(x) \frac{\partial N}{\partial x}(x,y)$$
Ninguna de las dos opciones es correcta.
$$\frac{\partial}{\partial y}(\mu(x) M(x,y))=\mu(x) \frac{\partial M}{\partial y}(x,y)$$
$$\frac{\partial}{\partial x}(\mu(x) N(x,y))=\mu'(x) \frac{\partial N}{\partial x}(x,y)$$
$$\frac{\partial}{\partial y}(\mu(x) M(x,y))=\mu(x) \frac{\partial M}{\partial y}(x,y)$$
$$\frac{\partial}{\partial x}(\mu(x) N(x,y))=\mu '(x) N(x,y)+\mu(x) \frac{\partial N}{\partial x}(x,y)$$
No es correcto, pues la función $\mu$ sólo depende de $x$ y no de $y$, luego no tiene sentido hablar de sus derivadas parciales.
Sí hay una correcta.
No es correcto, cuidado con la derivada del producto $\mu(x) N(x,y)$.
En efecto,
$$\frac{\partial}{\partial y}(\mu(x) M(x,y))=\mu(x) \frac{\partial M}{\partial y}(x,y) = \mu(x)\left(-6x+2\frac{y}{x}\right)$$
$$\frac{\partial}{\partial x}(\mu(x) N(x,y))=\mu '(x) N(x,y)+\mu(x) \frac{\partial N}{\partial x}(x,y) = 2\mu'(x)(y-x^2)+\mu(x)(-4x)$$
Una vez encontradas estas derivadas, el segundo paso es imponer que sean iguales para saber qué ecuación debe cumplir $\mu(x)$. Inténtalo y pulsa en 'Continuar'.
Paso 2
Igualando las derivadas parciales tendremos (obviamos la dependencia de $x$ para simplificar la escritura) $$\left(-6x+2\frac{y}{x}\right)\mu=-4x\mu+2(y-x^2)\mu' \hspace{1cm}\Rightarrow \hspace{1cm} 2(y-x^2)\mu'=2\frac{y-x^2}{x}\mu \hspace{1cm}\Rightarrow \hspace{1cm} \mu'=\mu\frac{1}{x}$$ Esta última expresión confirma la existencia de un factor integrante que sólo depende de $x$. El siguiente paso es resolver esta ecuación diferencial. Inténtalo y pulsa en 'Ver'.
Ver
Se trata de una ecuación separable en $\mu$ y $x$:
$$\mu'=\mu\frac{1}{x} \hspace{1cm}\Rightarrow \hspace{1cm} \frac{\mu'}{\mu}=\frac{1}{x}
\hspace{1cm}\Rightarrow \hspace{1cm} \log |\mu|=\log |x|+C$$
Luego cualquier función de la forma $\mu=Kx$ con $K\neq 0$ nos sirve como factor integrante de la ecuación inicial.
Resolución del tercer apartado
Para resolver la ecuación inicial, $\left(4x^2-6xy+\frac{y^2}{x}\right)\, dx+2(y-x^2)\, dy=0$, elegimos de entre los encontrados antes el factor integrante $$\mu(x)=x$$ de forma que el problema consiste ahora en resolver la ecuación exacta $$(4x^3-6x^2y+y^2)\, dx+2x(y-x^2)\, dy=0$$ para lo cual hemos de encontrar una función $u(x,y)$ tal que $du=(4x^3-6x^2y+y^2)\, dx+2x(y-x^2)\, dy$. Inténtalo y pulsa en 'Ver'.
Ver
Debe cumplirse que
$$u'_x(x,y)=4x^3-6x^2y+y^2 \hspace{1cm} ,\hspace{1cm} u'_y(x,y)=2(xy-x^3)$$
Integrando la primera, $$u(x,y)=x^4-2x^3y+xy^2+C(y)$$
y derivando esta expresión respecto de $y$,
$$u'_y(x,y)=-2x^3+2xy+C'(y)$$
Debe ocurrir que $$u'_y(x,y)=-2x^3+2xy+C'(y)=2(xy-x^3)$$
con lo cual $C'(y)=0$, es decir, $C$ es constante. Por tanto $$u(x,y)=x^4-2x^3y+xy^2+C$$
Por tanto la solución general de la ecuación inicial es
$u(x,y)=x^4-2x^3y+xy^2+C$
Ninguna de las opciones presentadas es correcta.
$x^3-2x^2y+y^2=\frac{C}{x}$
Hay más de una opción correcta.
$x^4-2x^3y+xy^2=K$
La solución general de una ecuación diferencial de primer orden es una familia, uniparamétrica, de curvas. En la propuesta que has elegido no hay curvas pues se trata de superficies (una distinta para cada valor de $C$). A continuación puedes ver dibujada la porción de la superficie correspondiente a $C=0$ sobre el rectángulo $[-10,10]\times[-5,5]$:
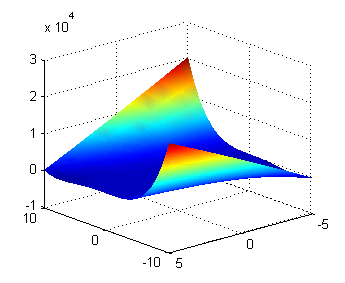
Una de las opciones es correcta.
¿Piensas que hay que dividir por el factor integrante? Pues no. La solución de $x(M\, dx+N\, dy)=0$ es la solución de $M\, dx+N\, dy=0$
Sólo una de las opciones es correcta.
En efecto, puesto que la ecuación diferencial es $du=0$, su solución general es $u=K$. Si por ejemplo tomamos $u(x,y)=x^4-2x^3y+xy^2$

Resolución del cuarto apartado
Puesto que las soluciones de la ecuación son las curvas de nivel de una superficie, podemos utilizar el comando 'contour' de la siguiente manera:[X,Y]=meshgrid(-10:10,-5:5); Z=X.^4-2*X.^3.*Y+X.*Y.^2; contour(X,Y,Z)
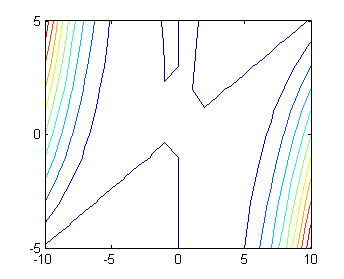
Resolución del quinto apartado
Debemos buscar la curva de la familia $x^4-2x^3y+xy^2=K$ que pasa por el punto $(1,2)$. Hazlo tú y pulsa en 'Ver' cuando la tengas.
Ver
Sustituyendo $x=1$ e $y=2$, tendremos que $K=1$, luego la solución particular pedida es
$$x^4-2x^3y+xy^2=1$$
Para representarla en el ordenador podemos recurrir al comando 'ezplot'. Ejecutando
f=@(x,y) x^4-2*x^3*y+x*y^2-1; ezplot(f) grid onse obtiene la figura
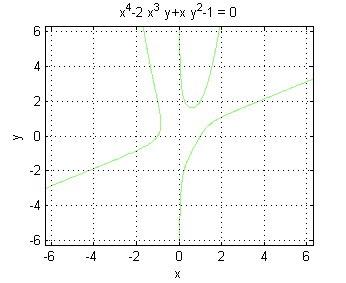
Resolución del sexto apartado
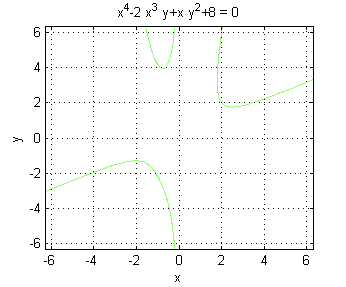
Igual que el apartado anterior, determinamos el valor de la constante para que la curva solución pase por el punto $(2,2)$, obteniendo $$x^4-2x^3y+xy^2=-8$$ Represéntala en el ordenador y pulsa en 'Ver'.
Ver
Ejecutando
f=@(x,y) x^4-2*x^3*y+x*y^2+8; ezplot(f) grid onse obtiene la figura