Enunciado
Dada la familia de curvas, expresadas en polares, $r=Ce^{\theta}$, se pide
- Escribe la expresión de la familia en coordenadas rectangulares, $(x,y)$, y obtén la ecuación diferencial ordinaria de primer orden cuya solución general es esa familia.
- Utiliza el apartado anterior para encontrar la familia de curvas que se cortan con la familia inicial formando un grado de $\pi/4$ radianes. Después expresa esta segunda familia en coordenadas polares.
- Dibuja en el ordenador las seis curvas $r=Ce^{\theta}$ para $C=-3:3$ y tres curvas de la familia oblicua calculada en el apartado anterior.
Resolución del primer apartado
Puesto que la relación entre las coordenadas polares y las cartesianes es
$$r=\sqrt{x^2+y^2}\hspace{1cm} ,\hspace{1cm} \theta=\mbox{arctg}\frac{y}{x}$$
la expresión cartesiana de la familia de curvas del enunciado es
$$\sqrt{x^2+y^2}=Ce^{\mbox{arctg}\frac{y}{x}}$$
Para obtener la ecuación cuya solución general es esa familia debemos derivar y eliminar el parámetro.
Paso 1
Derivar: esta derivación resulta más cómoda si previamente elevamos al cuadrado la expresión. Deriva el cuadrado de la expresión de la familia y pulsa en 'Ver'.
Ver
$$x^2+y^2=C^2e^{2\mbox{arctg}\frac{y}{x}}\hspace{1cm} \Rightarrow \hspace{1cm}
2x+2yy'=C^2\frac{2}{1+\frac{y^2}{x^2}}\frac{xy'-y}{x^2}e^{2\mbox{arctg}\frac{y}{x}}
\hspace{1cm} \Rightarrow $$
$$\Rightarrow \hspace{1cm} x+yy'=C^2\frac{xy'-y}{x^2+y^2}e^{2\mbox{arctg}\frac{y}{x}}$$
Paso 2
Eliminar el parámetro: puesto que el factor $C^2e^{2\mbox{arctg}\frac{y}{x}}$ está presente tanto en la expresión de la familia como en el de la derivada, podemos escribir $$x+yy'=\frac{xy'-y}{x^2+y^2}(x^2+y^2)$$ de donde obtenemos la ecuación buscada: $$y'=\frac{x+y}{x-y}$$Resolución del segundo apartado
Se trata de un problema de búsqueda de familia oblicua a una dada. El primer paso, encontrar la ecuación correspondiente a la familia inicial, ya está realizado en el apartado anterior. Debes por tanto encontrar ahora la ecuación correspondiente a la familia oblicua de ángulo $\beta=\pi/4$. Siguiendo la notación empleada en la teoría, $y_2$ es la nueva curva, $y_1$ es la inicial, que verifica $$y'_1=\frac{x+y}{x-y}$$ Intenta encontrar la ecuación diferencial para $y_2$ y pulsa en 'Ver'.
Ver
Puesto que $\mbox{tg}\beta=1$, se cumplirá $$y'_2=\frac{y'_1+1}{1-y'_1}$$ donde hemos de sustituir $y'_1$ en función de $x$ e $y$:
$$y'_2=\frac{\frac{x+y}{x-y}+1}{1-\frac{x+y}{x-y}}=\frac{2x}{-2y}=-\frac{x}{y}$$
La ecuación de las curvas oblicuas a $\pi/4$ radianes es por tanto
$$y'=-\frac{x}{y}$$
Sólo resta resolver esta ecuación, que es de variables separables:
$$y'=-\frac{x}{y} \hspace{1cm} \Rightarrow \hspace{1cm} y\,dy=-x\, dx \hspace{1cm} \Rightarrow \hspace{1cm}
y^2=-x^2+K \hspace{1cm} \Rightarrow \hspace{1cm} x^2+y^2=K$$
que en coordenadas polares es $r=C$. La familia inicial es una familia de espirales, las trayectorias que forman con ellas $\pi/4$ radianes son las circunferencias de centro el origen.
Resolución del tercer apartado
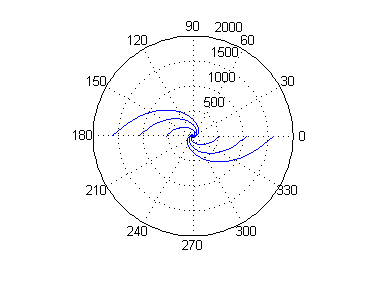
Para dibujar las seis curvas de $r=Ce^{\theta}$ para $C=-3:3$, podemos ejecutart=-2*pi:pi/50:2*pi; for c=-3:3 polar(t,c*exp(t)) hold on end
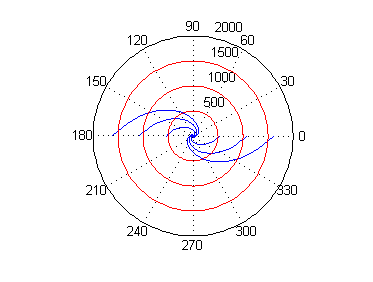
Superpondremos ahora tres curvas de la familia oblicua (circunferencias), trazándolas en otro color, por ejemplo en rojo. Si no observamos el dibujo anterior y tomamos por ejemplo $r=1$, $r=2$ y $r=3$, no se apreciará más que un punto rojo en el origen:
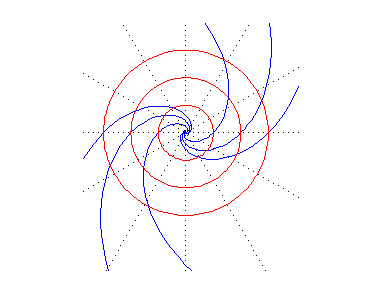
Si queremos ver las gráficas sin necesidad de aplicar zoom, podemos tomar radios mucho mayores como por ejemplo $r=500$, $r=1000$ y $r=1500$. Elige el código que añadiríamos al anterior para superponer las circunferencias a las espirales:
for c=1:3 polar(t,c*500,'r') end hold off
for c=1:3 polar(t,c*500*ones(length(t)),'r') end hold off
Todas las opciones dan error.
for c=1:3 polar(t,c*500*ones(size(t)),'r') end hold off
No es correcto, pues 'c*500' es un número, no un vector de la misma longitud que 't'
No es correcto, pues 'ones(length(t))' es una matriz cuadrada de dimensión la longitud de 't'
Hay una opción correcta.
Esta es correcta. Ejecutando todo se obtiene la figura