Enunciado
Se considera la ecuación diferencial de primer orden $$y'+y=2x+x^2$$
- Encuentra y representa la solución que pasa por el punto $(0,0)$.
- Encuentra y representa la solución que pasa por el punto $(1,0)$.
- Busca una solución que tenga un máximo y represéntala en el plano.
- ¿Existe alguna solución que tenga la primera y segunda derivadas nulas en algún punto?
Resolución del primer apartado
Paso 1
Encontrar la solución general de la ecuación: reconocemos que es lineal y que por tanto la podemos resolver mediante la aplicación del factor integrante . Encuentra la solución general aplicando ese método y pulsa en 'Ver'.
Ver
En este caso el factor integrante es $\mu(x)=e^x$ y por tanto la solución cumple que $$e^xy=\int (2x+x^2)e^x\, dx$$
Integrando por partes $x^2e^x$,
$$\int x^2e^x=x^2e^x-2\int xe^x\, dx$$
de donde $$e^x y=x^2e^x+C$$
y así la solución general es $$y=x^2+Ce^{-x}$$
Paso 2
Encontrar la solución particular: Inténtalo tú y pulsa en 'Ver'.
Ver
Imponiendo que $y=x^2+Ce^{-x}$ pase por $(0,0)$: $$y(0)=C=0 \hspace{1cm}\Rightarrow \hspace{1cm}y=x^2$$
A la figura con la gráfica de esta solución (en azul) le podemos añadir la curva formada por los puntos del plano donde la primera derivada de las soluciones es nula ($y=2x+x^2$ es la isoclina cero, en rojo) y la curva formada por los puntos del plano donde la segunda derivada es nula ($y=x^2-2$, en verde):
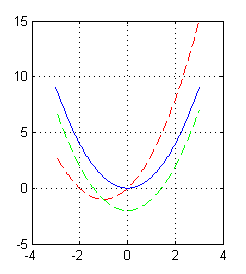
% curva solución pasando por (0,0), la roja es la iso. 0 y la verde y''=0 x=-3:.05:3; plot(x,x.^2,x,2*x+x.^2,'--r',x,x.^2-2,'--g') grid onPodemos observar que esta solución ($y=x^2$) es decreciente hasta que se corta con la isoclina cero (donde alcanza su mínimo) y que es siempre cóncava (está en la región $y>x^2-2$)
Resolución del segundo apartado
Tenemos la solución general, $y=x^2+Ce^{-x}$, determinada en el apartado anterior, luego pasamos directamente al cálculo de la solución particular: $$y(1)=1+Ce^{-1}=0\hspace{1cm}\Rightarrow \hspace{1cm} C=-e \hspace{1cm} \Rightarrow \hspace{1cm}y=x^2-e^{1-x}$$ Escribe el código con el que la dibujas en el ordenador para el intervalo $[-2,2]$, junto con la isoclina cero y la curva donde la segunda derivada de las soluciones es nula. Pulsa en 'Ver' cuando lo tengas
Ver
% curva solución pasando por (1,0), la roja es la iso. 0 y la verde y''=0 x=-2:.05:2; plot(x,x.^2-exp(1-x),x,2*x+x.^2,'--r',x,x.^2-2,'--g') grid on
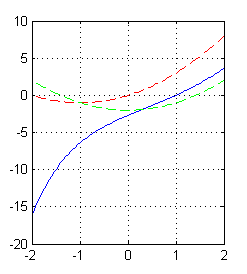
Resolución del tercer apartado
Debemos buscar una solución de la ecuación $y'+y=2x+x^2$ que tenga un máximo. Para ello...
Lo más adecuado es derivar la solución general e igualarla a cero.
Ninguna de las dos propuestas es correcta.
Lo mejor es utilizar directamente la ecuación y no la solución general.
No, esa no es la opción correcta.
Hay una opción correcta.
En efecto, la idea es construir una solución particular que pase por un punto del lugar geométrico donde las soluciones alcancen sus máximos. Puesto que la ecuación establece que $y'+y=2x+x^2$, los puntos extremos se alcanzan sobre la curva $y=2x+x^2$. Para buscar dónde se alcanzan los máximos, podemos calcular la segunda derivada de las soluciones e imponer que sea negativa. Inténtalo y pulsa en 'Continuar' cuando lo tengas.
$$y'=-y+2x+x^2\hspace{1cm}\Rightarrow \hspace{1cm} y''=-y' +2+2x \hspace{1cm}\Rightarrow \hspace{1cm} y''=2-x^2+y$$
Para los puntos de $y=2x+x^2$ será,
$$y''=2+2x$$
La segunda derivada es negativa en $x<-1$. Así que la solución buscada será ...
La que pasa por $(-2,1)$
La que pasa por $(-2,0)$
La que pasa por $(-3,3)$
Ninguna de las opciones presentadas es correcta.
Hay más de una opción correcta.
Si tomas $x=-2$, el valor de la segunda componente no puede ser 1 si quieres que este punto esté en la parábola $y=2x+x^2$, que es donde se alcanzan los extremos.
Esta opción es correcta, pero hay otra mejor.
Esta opción es correcta, pero hay otra mejor.
Sí hay una correcta.
En efecto, puede servirnos tanto la curva solución que pasa por $(-2,0)$ como la que pasa por $(-3,3)$, pues ambos son puntos de $y=2x+x^2$ con $x<-1$; podríamos tomar cualquiera que pase por un punto de la forma $(x,2x+x^2)$ con $x<-1$. Si elegimos la que pasa por $(-2,0)$, teniendo en cuenta que la solución general es $y=x^2+Ce^{-x}$,
$$y(-2)=4+Ce^2=0 \hspace{1cm} \Rightarrow \hspace{1cm} C=-4e^{-2}\hspace{1cm}
\Rightarrow \hspace{1cm} y=x^2-4e^{-(2+x)}$$
Obviamente el máximo se alcanzará en $x=-2$ y su valor será $0$.
Escribe el código para representarla en el intervalo $[-3,3]$ con el ordenador y pulsa en 'Continuar'.
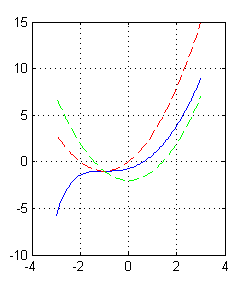
% curva solución pasando por (-2,0), la roja es la iso. 0 y la verde y''=0 x=-3:.05:3; plot(x,x.^2-4*exp(-(2+x)),x,2*x+x.^2,'--r',x,x.^2-2,'--g') grid on
Resolución del cuarto apartado
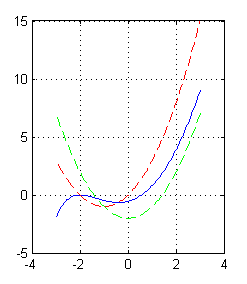
Debemos responder a la pregunta siguiente: ¿Existe alguna solución que tenga la primera y segunda derivadas nulas en algún punto? Para saberlo basta cortar las curvas donde se anulan esas derivadas:- $y'=0$: $y=2x+x^2$
- $y''=0$: $y=x^2-2$
Ver
Puesto que la solución general es $y=x^2+Ce^{-x}$,
$$y(-1)=1+Ce=-1 \hspace{1cm} \Rightarrow \hspace{1cm} C=-2e^{-1}\hspace{1cm}
\Rightarrow \hspace{1cm} y=x^2-2e^{-(1+x)}$$
% curva solución pasando por (-1,-1), la roja es la iso. 0 y la verde y''=0 x=-3:.05:3; plot(x,x.^2-2*exp(-(1+x)),x,2*x+x.^2,'--r',x,x.^2-2,'--g') grid on