Enunciado
Se considera la ecuación diferencial de primer orden $$y'+y=2(x+1)$$
- Comprueba que verifica las condiciones suficientes de existencia y unicidad de solución por cada punto $(x_0,y_0)$ del plano.
- Encuentra las regiones del plano donde sus soluciones son crecientes y donde son decrecientes. Analiza la existencia de extremos; en caso de existir determina su lugar geométrico en el plano y qué tipo de extremos son.
- Analiza la concavidad de las soluciones de la ecuación y la existencia y situación de puntos de inflexión.
- Contesta a la siguiente pregunta sin resolver la ecuación: la solución que pasa por el punto $(4,0)$ ¿es la misma que la que pasa por $(0,4)$?
Resolución del primer apartado
Tenemos que sabernos el teorema de
existencia y unicidad de solución de un p.v.i de primer orden.
Escribimos la ecuación como $$y'=f(x,y)=-y+2(x+1)$$ Comprueba que se cumplen las hipótesis y pulsa en 'Ver'.
Ver
Las hipótesis se cumplen puesto que:
- la función $f(x,y)=-y+2(x+1)$ es continua en todo el plano
- su derivada parcial respecto de $y$ es $f'_y(x,y)=-1$, que obviamente es continua en todo el plano
Resolución del segundo apartado
Utiliza la ecuación para hacer el análisis del comportamiento de las soluciones, no es preciso resolverla para saber el signo de la derivada en cada punto en función de las coordenadas $(x,y)$ del punto. Inténtalo y pulsa en 'Continuar'.
Las soluciones son crecientes donde su derivada sea positiva:
$$y'=-y+2(x+1)>0 \hspace{1cm} \Longrightarrow \hspace{1cm} y<2(x+1)$$
Esto quiere decir que las soluciones son crecientes cuando pasan por la región $y<2(x+1)$ y son decrecientes cuando pasan por la región $y>2(x+1)$. En cuanto a los extremos, teniendo en cuenta el teorema de existencia y unicidad y que la primera derivada de las soluciones se anula en la recta $y=2(x+1)$ ...
$y=2(x+1)$ no es solución, luego no existen extremos
$y=2(x+1)$ es solución, luego no existen extremos
$y=2(x+1)$ no es solución, luego existen extremos
En efecto $y=2(x+1)$ no es solución, pero la conclusión no es acertada.
$y=2(x+1)$ no es solución, pues para ella $y'=2$, mientras que $y-2(x+1)=0$
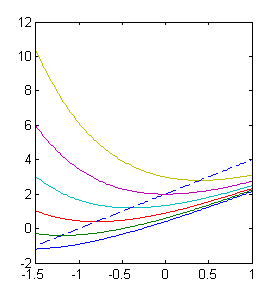
$y=2(x+1)$ no es solución, pues para ella $y'=2$, mientras que $y-2(x+1)=0$. Puesto que por los puntos de $y=2(x+1)$ deben pasar soluciones, éstas soluciones tendrán sus extremos cuando la corten. Estos extremos serán mínimos, pues las soluciones pasan de decrecientes a crecientes. En la siguiente figura puedes ver cómo una muestra de soluciones alcanzan sus mínimos cuando cortan a la recta $y=2(x+1)$.
Resolución del tercer apartado
Debemos ahora hacer el análisis de la concavidad. Igual que para la monotonía, no se requiere encontrar las soluciones, sino únicamente utilizar la ecuación diferencial. Intenta este análisis y pulsa en 'Ver'.
Ver
Escribimos $y''$ en función de $x$ e $y$, derivando la ecuación diferencial:
$$y'=-y+2(x+1) \hspace{1cm}\Rightarrow \hspace{1cm} y''=-y'+2=y-2(x+1)+2=y-2x$$
Por tanto, las soluciones son cóncavas en la región $y>2x$ y convexas en $y<2x$. ¿Existen puntos de inflexión? Analízalo y pulsa en 'Continuar'
Por cada punto de la recta $y=2x$ debe pasar una solución. Lo que ocurre en este caso es que la propia función $y=2x$ es solución de la ecuación:
$$y=2x \hspace{1.5cm} \Longrightarrow \hspace{1.5cm} \left\{\begin{array}{l}y'=2\\ -y+2(x+1)=-2x+2x+2=2\end{array}\right.$$
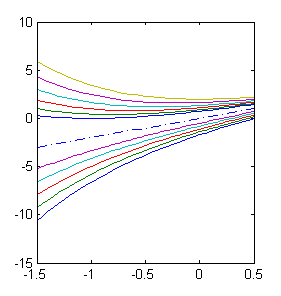
puesto que se verifica el teorema de unicidad de solución por cada punto del plano, por los puntos de $y=2x$ no pasa ninguna otra solución. En la siguiente figura podemos ver el comportamiento de una muestra de soluciones: por encima de $y=2x$ (en trazo discontinuo) son cóncavas y por debajo de $y=2x$ son convexas:
Resolución del cuarto apartado
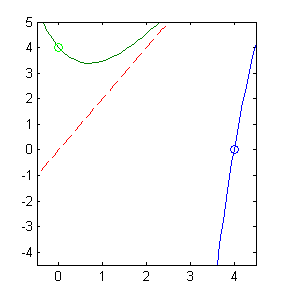
El punto $(4,0)$ está en el semiplano $y<2x$ mientras que $(0,4)$ está en $y>2x$. En el apartado anterior vimos que las curvas solución no cortan a $y=2x$, por lo tanto la solución que pasa por $(4,0)$ debe esr necesariamente diferente de la que pasa por $(0,4)$. En la siguiente figura se ha trazado una parte de cada una de estas curvas: