Enunciado
- Dos depósitos con orificios de salida idénticos en sus fondos están inicialmente llenos de agua. Uno es cilíndrico de eje vertical y el otro es un semicono con su vértice abajo. Si las bases son iguales y tardan el mismo tiempo en vaciarse, ¿cuál es la relación entre la altura $h$ del cilíndrico y la altura $H$ del cónico?
- Tomamos ahora un tanque semiesférico con la misma base y orificio de salida que los anteriores. ¿Sería posible que se vaciara en el mismo tiempo?
Primer apartado
En primer lugar establecemos la notación que utilizaremos en toda la resolución:
- $S$: área de la base de los depósitos;
- $s$: área del orificio de salida;
- $t$: tiempo (variable independiente del modelo);
- $x(t)$: altura de agua en el depósito en el momento $t$;
- $V(t)$: volumen de agua en el depósito en el momento $t$;
- la tasa de entrada de agua al depósito es nula en estos casos, pues en el enunciado no se indica entrada de agua;
- la tasa de salida de agua del depósito se establece teniendo en cuenta que
- el volumen que sale por unidad de tiempo es el producto de la velocidad de salida por el área del orificio y
- la velocidad de salida es la misma que si el agua cayera desde el nivel de agua hasta el orificio (Ley de Torricelli): $\sqrt{2g x(t)}$, siendo $g$ la aceleración de la gravedad.
Ver
$$\frac{dV}{dt}=-s\sqrt{2g x(t)}$$
Ahora debemos poner todo en términos de $x(t)$, para lo cual es preciso escribir $V(t)$ en función de $x(t)$. Esto será diferente según cuál sea la forma del depósito.
Depósito cilíndrico
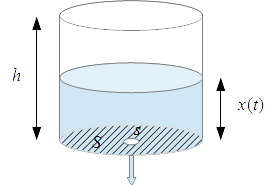
Puesto que se trata de un cilindro de base $S$, el volumen en cada momento es $V(t)=Sx(t)$, luego la ecuación diferencial es en este caso $$\frac{dx}{dt}(t)=-\frac{s}{S}\sqrt{2g}\sqrt{x(t)}$$ Esta ecuación se acompaña de la condición inicial ..., escríbela y pulsa en 'Ver'.
Ver
Obviamente, $x(0)=h$, pues el enunciado establece que el depósito inicialmente está lleno.
La solución del problema de valor inicial
$$\frac{dx}{dt}(t)=-\frac{s}{S}\sqrt{2g}\sqrt{x(t)}\ \ ,\ \ x(0)=h$$ es
$$x^{-3/2}=\frac{2s}{S}\sqrt{2g}t$$
$$\sqrt{x}=\frac{-s}{2S}\sqrt{2g}t$$
Ninguna de las opciones presentadas es correcta.
$$\sqrt{x}=\frac{-s}{2S}\sqrt{2g}t+\sqrt{h}$$
No, repasa la integración que realizas una vez que separas las variables.
No, repasa la integración que realizas una vez que separas las variables.
No, hay una opción correcta.
En efecto, esa es la solución del problema de valor inicial, pues la solución general de la ecuación es $$\sqrt{x}=\frac{-s}{2S}\sqrt{2g}t+C$$
y al imponer que $x(0)=h$, resulta $C=\sqrt{h}$. Una vez que, para este depósito cilíndrico, sabemos la expresión de la altura de agua en función del tiempo,
el último paso es hallar el tiempo $t_f$ que tarda en vaciarse. Hazlo y pulsa en 'Ver'.
$$x(t_f)=0\ \ \Rightarrow\ \ \frac{-s}{2S}\sqrt{2g}t_f+\sqrt{h}=0\ \ \Rightarrow\ \ t_f=\frac{2S\sqrt{h}}{s\sqrt{2g}}$$
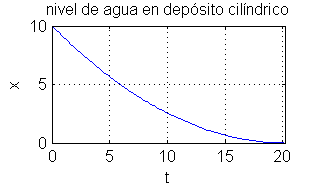
Por ejemplo, para $S=9\pi^2$, $s=2$ y $h=10$, el tiempo que tarda en vaciarse es aprox. $t_f=20.2$:
Depósito cónico
Un esquema de este depósito podría ser: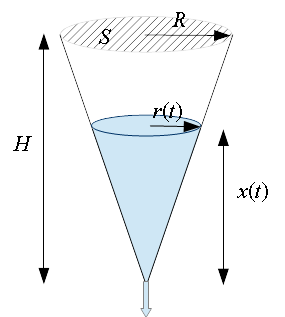
- El radio $R$ del depósito, que podemos escribir en términos de la dimensión $S$, pues $S=\pi R^2$.
- La variable radio del semicono ocupado por agua, $r(t)$, nos servirá como intermediaria para escribir el volumen de agua $V(t)$ en función de nuestros datos, $S$ y $H$ y nuestra incógnita, $x(t)$.
Continuar
Utilizando semejanza de triángulos,
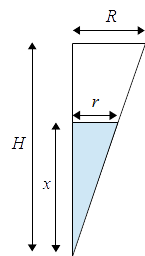
Derivando $V(t)=\frac{1}{3}\frac{S}{H^2}x(t)^3$ tendremos $$\frac{S}{H^2}x(t)^2\frac{dx}{dt}=-s\sqrt{2g}\sqrt{x(t)}\ \ ,\ \ x(0)=H$$
Encuentra la solución de la ecuación y pulsa en 'Ver'.
Ver
Separando las variables encontramos que la solución general de la ecuación es $$x^{5/2}=\frac{-5s}{2S}H^2\sqrt{2g}t+C$$
y al imponer que $x(0)=H$, resulta $C=H^{5/2}$, luego la solución del problema de valor inicial es
$$x^{5/2}=\frac{-5s}{2S}H^2\sqrt{2g}t+H^{5/2}$$
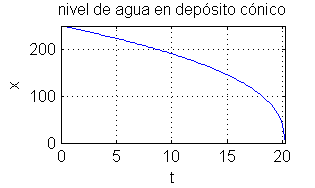
De la expresión de $x(t)$ obtenemos el tiempo $t_f$ que tarda el depósito en vaciarse, $$x(t_f)=0\ \ \Rightarrow\ \ \frac{-5s}{2S}H^2\sqrt{2g}t_f+H^{5/2}=0\ \ \Rightarrow\ \ t_f=\frac{2S\sqrt{H}}{5s\sqrt{2g}}$$
Ya tenemos lo que tarda cada depósito en vaciarse en términos de sus alturas respectivas. Puesto que se vacían en el mismo tiempo, la relación entre las alturas es ... Encuéntrala y pulsa en 'Ver'.
Ver
$$\frac{2S\sqrt{h}}{s\sqrt{2g}}=\frac{2S\sqrt{H}}{5s\sqrt{2g}}\ \ \Rightarrow\ \ \sqrt{h}=\frac{\sqrt{H}}{5}\ \ \Rightarrow\ \ H=25h$$
Segundo apartado
En el tanque semiesférico, obviamente el radio $R$ es igual a la altura $h$; la tasa de cambio de volumen viene igualmente dada por $\frac{dV}{dt}=-s\sqrt{2g x(t)}$, pues este hecho no depende de la forma del depósito, siempre que el orificio esté en su fondo.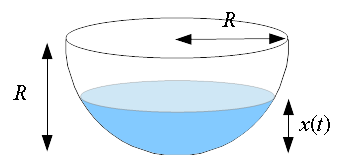
$V(t)=\frac{2}{3}\pi x(t)^3$
$V(t)=\frac{2}{3}\pi(R^3- x(t)^3)$
$V(t)=\frac{2}{3}\pi(R- x(t))^3$
Ninguna de las propuestas es correcta.
No, la parte ocupada por agua no es una semiesfera.
No, míralo bien; el agua ocupa un casquete esférico.
No, míralo bien; el agua ocupa un casquete esférico.
En efecto, ninguna de las propuestas es correcta. Para hallar $V(t)$ podemos utilizar que el volumen de un sólido de sección transversal conocida, como es la parte del depósito ocupada por agua, se obtiene como la integral del área de esas secciones. En este caso cada sección perpendicular al radio vertical del depósito es un círculo. Dibujamos el perfil correspondiente a una altura $u$. Si llamamos $r$ al radio del círculo correspondiente a altura $u$, tendremos un triángulo rectángulo de catetos $r$ y $R-u$ e hipotenusa $R$:
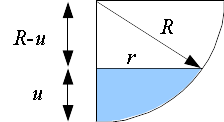
$$r^2+(R-u)^2=R^2 \ \ \Rightarrow\ \ r^2=R^2-(R-u)^2=2Ru-u^2$$
Por tanto, el volumen ocupado por agua es $$V(t)=\int_0^{x(t)}A(u)\, du=\int_0^{x(t)}\pi(2Ru-u^2)\, du$$
Esta integral puede calcularse, pero no es preciso hacerlo si utilizamos el Teorema Fundamental del Cálculo Integral, pues realmente lo que nos hace falta no es $V(t)$ sino su derivada. Así pues,
$$\frac{dV}{dx}=\pi(2R x(t)-x(t)^2)$$
$$\frac{dV}{dt}=\pi(2R x(t)-x(t)^2)$$
$$\frac{dV}{dt}=\pi(2R-2x(t))$$
$$\frac{dV}{dt}=\pi(2R x(t)-x(t)^2)\frac{dx}{dt}$$
No, aunque la derivada es correcta, no es la que se busca.
No, el extremo de integración no coincide con la variable de integración.
No, repasa el Teorema Fundamental del Cálculo Integral.
Así es, pues por la regla de la derivación compuesta, $$\frac{dV}{dt}=\frac{dV}{dx}\frac{dx}{dt}$$
Escribe ahora el problema de valor inicial que verifica $x(t)$, resuélvelo y pulsa en 'Continuar'.
El problema es
$$\pi(2R x(t)-x(t)^2)\frac{dx}{dt}=-s\sqrt{2g}\sqrt{x} \ \ ,\ \ x(0)=R$$
Separando las variables en la ecuación e integrando,
$$(2R\sqrt{x}-x^{3/2})\, dx=-\frac{s\sqrt{2g}}{\pi}\, dt \ \ \Rightarrow\ \ \left(\frac{4}{3}Rx-\frac{2}{5}x^2\right)\sqrt{x}=-\frac{s\sqrt{2g}}{\pi}\, t+C$$
y utilizando la condición inicial,
$$x(0)=R\ \ \Rightarrow\ \ \left(\frac{4}{3}R^2-\frac{2}{5}R^2\right)\sqrt{R}=C\ \ \Rightarrow\ \ C=\frac{14}{15}R^{5/2}$$
llegamos a la solución final $$\left(\frac{4}{3}Rx-\frac{2}{5}x^2\right)\sqrt{x}=-\frac{s\sqrt{2g}}{\pi}\, t+\frac{14}{15}R^{5/2}$$
Ver
$$x(t_f)=0\ \ \Rightarrow\ \ \frac{s\sqrt{2g}}{\pi}\, t_f=\frac{14}{15}R^{5/2} \ \ \Rightarrow\ \ t_f=\frac{14}{15}\frac{\pi}{s\sqrt{2g}}R^{5/2}$$
o bien, si tenemos en cuenta que $\pi R^2=S$, $$t_f=\frac{14}{15}\frac{S}{s\sqrt{2g}}\sqrt{R}$$
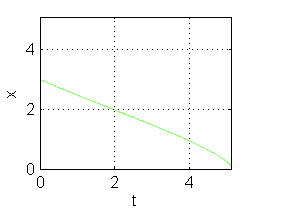
El tiempo de vaciado del depósito cilíndrico era $2\frac{S}{s\sqrt{2g}}\sqrt{h}$. Puesto que en la semiesfera existe una ligadura entre el área $S$ y la altura $h$, no podría encontrase un tanque semiesférico que se vaciara en el mismo tiempo que el cilindro. El tiempo que tardaba en vaciarse el depósito cílíndrico, de magnitudes $S=9\pi^2$, $s=2$ y $h=10$, era aprox. $t_f=20.2$; el depósito esférico de parámetros $S=9\pi^2$ y $s=2$ tardará aprox. 5.2 unidades de tiempo en vaciarse.