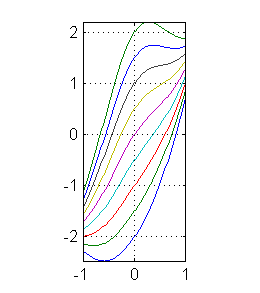
Enunciado
Se considera la ecuación $$y'+2y\,\mbox{tg}\, x=3x\mbox{tg}\, x+1$$
- Encuentra el lugar geométrico de los puntos del plano donde sus soluciones tienen pendiente 1.
- Comprueba que la ecuación verifica el teorema de existencia y unicidad de solución en cada punto de la forma $(0,y_0)$.
- Analiza la concavidad de las soluciones a su paso por los puntos de la forma $(0,y_0)$.
Resolución del primer apartado
Puesto que la pendiente de la gráfica de $y=(x)$ en el punto $(x_0,f(x_0))=(x_0,y_0)$ es $y'(x_0)$, la ecuación que deben verificar $x_0$ e $y_0$ para que una solución $y(x)$ tenga pendiente 1 en el punto $(x_0,y_0)$ es ... Piénsalo y pulsa en 'Ver'.
Ver
Sustituyendo en la ecuación $x$ por $x_0$, $y$ por $y_0$ e $y'$ por 1, obtendremos $$\mbox{tg}\, x_0(2y_0-3x_0)=0$$
De aquí deducimos que
$$2y_0=3x_0 \ \ \ \Rightarrow\ \ \ y_0=\frac{3}{2}x_0$$ Los puntos buscados son los de la recta $y=\frac{3}{2}x$.
Los puntos buscados son los de la recta $y=\frac{3}{2}x$ junto con el eje $x=0$, pues de $\mbox{tg}\, x_0=0$ se deduce que $x_0=0$.
Ninguna de las dos propuestas es correcta.
No, ten en cuenta queun producto se anula cuando al menos uno de los factores se anula: faltan puntos si sólo tomas $y=\frac{3}{2}x$.
No, además de $x_0=0$ hay más valores que cumplen la ecuación $\mbox{tg}\, x_0=0$.
En efecto, las otras dos propuestas son incompletas, ¿para qué valores de $x$ se anula $\mbox{tg}\, x$? Piénsalo y pulsa en 'Continuar'.
$$\mbox{tg}\, x=0 \ \ \Rightarrow \ \ x=n\pi,\ \ n\in{\bf Z}$$
Por tanto el lugar geométrico buscado es la unión de la recta $y=\frac{3}{2}x$ y todas las rectas verticales de la forma $x=n\pi$ para $n$ entero.
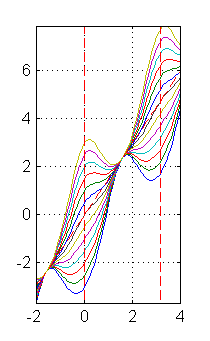
Resolución del segundo apartado
Para poder utilizar el teorema de existencia y unicidad de solución de un p.v.i de primer orden hemos de escribir la ecuación en forma explícita $y'=f(x,y)$. Pulsa en 'Continuar' cuando lo tengas.
La ecuación es $y'=(3x-2y)\mbox{tg}\, x+1$
luego $$f(x,y)=(3x-2y)\mbox{tg}\, x+1$$
Sabemos que para cada elección de $y_0$, el p.v.i. $$y'=f(x,y)\ \ ,\ \ y(0)=y_0$$ tiene solución única porque
$f(0,y_0)=1$ es una función continua con derivada respecto de $y$ también continua.
No se debe a la razón expuesta en la otra opción.
$f(0,y_0)$ no es una función, es un número; no es así como se analiza la existencia y unicidad. Vuelve a revisar el teorema
Claro, debe analizarse la continuidad de la función $f(x,y)$ sin sustituirla en el punto. Hazlo y pulsa.
$f(x,y)=(3x-2y)\mbox{tg}\, x+1$ es continua en un entorno de cualquier punto $(0,y_0)$ de la forma $[a,b]\times[c,d]$ siempre que $[a,b]$ no se salga de $(\frac{-\pi}{2},\frac{\pi}{2})$. Además ${f'}_y(x,y)=-2\mbox{tg}\, x$ también es continua en un entorno de ese tipo. Por tanto se cumplen las condiciones del teorema de existencia y unicidad.
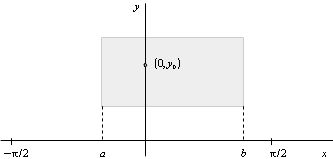
Resolución del tercer apartado
El signo de $y''(0)$ indica el tipo de concavidad, pues si $y''(0)>0$, entonces la gráfica es cóncava hacia arriba en el punto $(0,y_0)$, si $y''(0)<0$, entonces la gráfica es cóncava hacia abajo en el punto $(0,y_0)$ y si $y''(0)=0$, entonces el punto $(0,y_0)$ es de inflexión.
Eso es incorrecto.
Eso es correcto.
¿Seguro? Míralo bien.
En efecto, es correcto. Debemos por tanto obtener $y''(0)$, pero no contamos con la función $y=y(x)$. Piensa cómo hallar ese valor y pulsa en 'Continuar'
Hemos de derivar la ecuación diferencial $y'=(3x-2y)\mbox{tg}\, x+1$:
$$y'=(3x-2y)\mbox{tg}\, x+1\ \ \ \Rightarrow\ \ \ y''=(3-2y')\mbox{tg}\, x$$
$$y'=(3x-2y)\mbox{tg}\, x+1\ \ \ \Rightarrow\ \ \ y''=(3-2y')\mbox{tg}\, x+\frac{3x-2y}{1+x^2}$$
Ninguna de las propuestas es correcta.
$$y'=(3x-2y)\mbox{tg}\, x+1\ \ \ \Rightarrow\ \ \ y''=(3-2y')\mbox{tg}\, x+(3x-2y)(1+\mbox{tg}^2\, x)$$
No está bien derivado, puesto que $(3x-2y)\mbox{tg}\, x$ es producto de funciones de $x$.
No, revisa la derivada de $\mbox{tg}\, x$.
No, revísalas pues sí hay una correcta.
Sí, así es. Ahora podemos sustituir $x=0$ en esa expresión; el valor de $y'(0)$ lo obtendríamos si fuera necesario de la propia ecuación diferencial. Hazlo y pulsa cuando termines.
$$y''(0)=(3-2y'(0))\mbox{tg}\, 0-2y(0)(1+0)\ \ \ \Rightarrow\ \ \ y''(0)=-2y(0)$$
Por tanto podemos concluir que
- Si $y(0)>0$, entonces la función en el punto $(0,y_0)$ es cóncava hacia abajo
- Si $y(0)<0$, entonces la función en el punto $(0,y_0)$ es cóncava hacia arriba
- El punto $(0,0)$ es de inflexión para la curva solución que pasa por él.