Índice de tema

 

Enunciado

En un reactor 'semibatch' se introduce de forma continua el reactivo, pero la salida no se produce de forma continua. Supongamos que la sustancia $A$ reacciona proporcionalmente al cuadrado de su concentración y que en el momento $t=0$ comienza a alimentarse el reactor con un fluido a razón de $F^e$ L$/$seg con una concentración $C^e$ moles$/$L. Inicialmente el reactor tenía un volumen de $V_0$ litros de un líquido inerte.
  1. Encuentra un modelo diferencial para la cantidad de sustancia $A$ en el reactor.
  2. Supongamos que $F^e=2$ L$/$seg, $C^e=0.7$ moles$/$L, $V_0=20$ L y $k=0.2$ L$/$moles$\cdot$seg. Aproxima la cantidad de sustancia $A$ durante el primer minuto, con un intervalo de un segundo, utilizando el comando 'ode45'. Representa la solución estimada.
  3. Prepara una función para el ordenador que aproxime la solución de un problema de valor inicial mediante el método de Euler mejorado y aplícala para estimar la cantidad de sustancia $A$ de segundo en segundo durante el primer minuto. Dibuja en una misma figura esta aproximación junto con la del apartado anterior.
  4. Nos centramos ahora en la aproximación de la cantidad de sustancia en $t=60$. Compara las estimaciones realizadas con el método de Euler mejorado tomando pasos $h=4$, $h=2$, $h=1$ y $h=0.5$. Representa esos cuatro valores en una gráfica.
  5. Para este problema podemos ganar cierta exactitud, por ejemplo ajustar la tercera cifra decimal, reduciendo el valor de $h$. Si empezamos en $h=4$ y vamos dividiendo por 2 el valor del paso, ¿cuál será el primero de ellos para el cual se garantizan tres cifras decimales?

Resolución del primer apartado

Comenzamos estableciendo nombres a las variables de nuestro problema:
  • n(t): cantidad, en moles, de sustancia $A$ presente en el reactor en el tiempo $t$;
  • V(t): volumen de líquido en el reactor, en litros.
  • C(t): concentración de $A$ por unidad de volumen en el reactor.
El balance molar de $A$ correspondiente a una parte diferencial de tiempo, $dt$, será $$\begin{array}{cccccccccc}\mbox{introducido}&-&\mbox{consumido}&+&\mbox{generado} &=&\mbox{extraído}&+&\mbox{acumulado} & \\ & & & & & & & & & \\ F^eC^e\ dt &-& k C^2V\ dt &+& 0 &=& 0 &+& dn & \ \ (\mbox{moles}) \end{array}$$ Deduce desde aquí la ecuación diferencial que cumple $n$ y pulsa en 'Ver'.
Ver
Para escribir esta expresión utilizando $n$, pensemos que $C=\frac{n}{V}$, luego $$\frac{dn}{dt}=F^eC^e-\frac{kn^2}{V}$$ Teniendo en cuenta que $V=V_0+F^et$, la ecuación que rige el número de moles acumulados de $A$ es $$\frac{dn}{dt}=F^eC^e-\frac{kn^2}{V_0+F^et}$$ con la condición inicial $n(t)=0$ para $t=0$.

Resolución del segundo apartado

Con los datos indicados, el problema de valor inicial general anterior se convierte en $$\frac{dn}{dt}=1.4-0.04\frac{n^2}{4+t} \hspace{1cm} , \hspace{1cm} n(0)=0$$ Los argumentos de entrada de 'ode45' para la aproximación de la solución del problema $$n'=f(t,n) \hspace{1cm} , \hspace{1cm} n(t_0)=n_0$$ son
  • la función $f$ definida previamente con la '@'
  • el vector de valores de $t$ donde quiera aproximarse la solución, que debe empezar en $t_0$
  • el valor $n_0$
Podemos pedirle como variable de salida un vector que tenga en su primera componente los valores del tiempo y en su segunda componente los valores de la aproximación. Abre un fichero .m y escribe en él las líneas que se van indicando, pulsando 'Continuar' cuando hayas escrito cada una.
  • empieza definiendo la función 'f' de nuestro problema
f=@(t,n) 1.4-0.04*n^2/(4+t);
  • utiliza 'ode45' como se indicó antes
[vt,nest]=ode45(f,0:60,0)
  • representa 'nest' frente al tiempo
plot(vt,nest)
xlabel('tiempo (seg)');
ylabel('sustancia A (moles)')
  • muestra por pantalla el vector de aproximaciones
nest
Escrito todo seguido, con comentarios añadidos resulta 
f=@(t,n) 1.4-0.04*n^2/(4+t); % definición de la función de la edo
[vt,nest]=ode45(f,0:60,0);   % aproximación durante el primer minuto, cada segundo
plot(vt,nest)                % representación de la estimación frente al tiempo
xlabel('tiempo (seg)');ylabel('sustancia A (moles)') % etiquetas de los ejes
nest                        % valor de la estimación
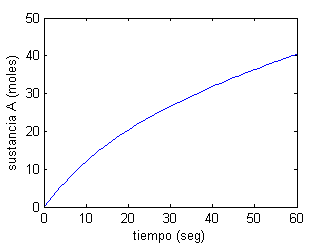
Cuando lo ejecutemos, mostrará en la ventana de comandos un vector columna de 61 componentes, que comienza con el valor 0 (pues $n(0)=0$) y continúa con la aproximación de $n(t)$ para cada segundo hasta la aproximación de $n(60)$, que es 40.3422; además se generará la figura

Gráfica

Resolución del tercer apartado

Una idea razonable para generar una función que implemente el método de Euler mejorado puede ser tomar como punto de partida la correspodiente al método de Euler que se preparó en otro ejercicio; puesto que la que se pide ahora no incluye la gráfica de la aproximación, podríamos dejarla en 
function y=aproxEuler(f,h,x0,y0,xf)
nmax=round((xf-x0)/h);
x=x0:h:xf;
y=y0*ones(size(x));
for n=1:nmax
    y(n+1)=y(n)+h*f(x(n),y(n));
end
end
Además del nombre, ¿qué hemos de modificar en esta función para adaptarla al método de Euler mejorado? Piénsalo y pulsa en 'Ver'.
Ver 
function y=aproxEulermej(f,h,x0,y0,xf)
nmax=round((xf-x0)/h);
x=x0:h:xf;
y=y0*ones(size(x));
for n=1:nmax
	aux=y(n)+h*f(x(n),y(n));
    y(n+1)=y(n)+h*(f(x(n),y(n))+f(x(n+1),aux))/2;
end
end
Guardaremos esta función en un fichero llamado 'aproxEulermej.m'. Piensa cómo se ejecuta esta función para que aproxime la solución del problema durante el primer minuto, cada segundo. Pulsa en 'Continuar' cuando lo tengas.
Debemos ejecutar 
est1=aproxEulermej(f,1,0,0,60)
siempre que tengamos ya definida la función 'f'. Podemos añadir esa línea en el fichero utilizado en el apartado anterior, cuando se estimó la solución mediante 'ode45' y completarlo con la representación de la gráfica de la nueva estimación; si calculamos la estimación por Euler mejorado antes de dibujar la estimada con 'ode45' podemos representarlas juntas con un mismo 'plot': 
f=@(t,n) 1.4-0.04*n^2/(4+t); % definición de la función de la edo
[vt,nest]=ode45(f,0:60,0);   % aproximación durante el primer minuto, cada segundo
nest1=aproxEulermej(f,1,0,0,60) % estimación con Euler mejorado, h=1
plot(vt,nest,vt,nest1)          % representación de las estimaciones frente al tiempo
xlabel('tiempo (seg)');ylabel('sustancia A (moles)') % etiquetas de los ejes
Podemos comparar alguna de estas aproximaciones: con 'ode45' el valor estimado para $n(60)$ es $40.3422$ mientras que con Euler mejorado, paso $h=1$, es $40.3405$.
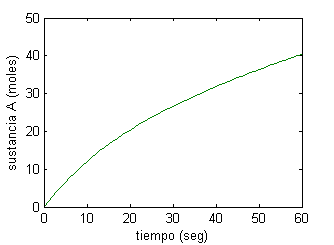
La ventana de figura mostrará

Gráfica

Observamos que las dos aproximaciones se superponen, puesto que las diferencias son demasiado pequeñas para la escala del eje vertical (cantidades).

Resolución del cuarto apartado

Debemos utilizar cuatro veces la función 'aproxEulermej', cambiando el valor de $h$ como corresponda e ir guardando esas aproximaciones; puesto que sólo se pide comparar el último valor de cada aproximación, guardaremos esos cuatro valores en un vector, que luego representaremos frente a $t=60$: 
f=@(t,n) 1.4-0.04*n^2/(4+t); % definición de la función de la edo
nest4=aproxEulermej(f,4,0,0,60) % estimación con Euler mejorado, h=4
nest2=aproxEulermej(f,2,0,0,60) % estimación con Euler mejorado, h=2
nest1=aproxEulermej(f,1,0,0,60) % estimación con Euler mejorado, h=1
nest05=aproxEulermej(f,.5,0,0,60); % estimación con Euler mejorado, h=0.5
valores=[nest4(end) nest2(end) nest1(end) nest05(end)]
plot(60,valores,'*')          % representación de las estimaciones frente al tiempo
xlabel('tiempo (seg)');ylabel('sustancia A (moles)') % etiquetas de los ejes
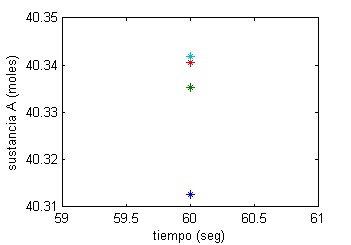
En la ventana de comandos mostrará 
valores =

   40.3126   40.3354   40.3405   40.3418
y en la de figuras,

Gráfica

Resolución del quinto apartado

En este apartado prepararemos un fichero con las líneas que calculan la aproximación de $n(60)$ tomando pasos decrecientes, en particular el paso se irá dividiendo entre 2, hasta conseguir que la diferencia entre una estimación y la siguiente diste menos de $10^{-4}$. Iremos construyendo ese fichero paso a paso: cuando hayas escrito la línea o líneas que se indican, pulsa en 'Continuar'.
  • Define la función $f$ de la ecuación diferencial, con la @, e inicializa $h$ como 4:
f=@(t,n) 1.4-0.04*n^2/(4+t);
h=4;
  • calcula la aproximación de los valores de $n$ entre 0 y 60, paso $h$, con la función 'aproxEulermej' anterior; llama 'nest' a esta aproximación
nest=aproxEulermej(f,h,0,0,60);
  • 'nest' es un vector; escribe la línea con la que se escribe su última componente en la ventana de comandos; esta componente es la aproximación de $n(60)$
nest(end)
  • inicializa una variable, 'diferencia', como $0.1$; esta variable guardará la diferencia entre sucesivas aproximaciones de $n(60)$
diferencia=.1;
  • abre un ciclo 'while' con la condición de que 'diferencia' sea mayor que $10^{-4}$ 
while diferencia>10^(-4)
  • a continuación prepararemos el cuerpo de este ciclo 'while'; lo primero es dividir el paso por 2, manteniendo obviamente su nombre: 
h=h/2;
  • guarda en un nuevo vector, 'nestsig', la aproximación con 'aproxEulermej' para este valor de 'h'
nestsig=aproxEulermej(f,h,0,0,60);
  • muestra en la ventana de comandos el valor estimado para $n(60)$
nestsig(end)
  • actualiza el valor de 'diferencia' 
diferencia=abs(nest(end)-nestsig(end))
  • guarda en 'nest' el vector 'nestsig'
nest=nestsig;
  • cierra el ciclo 'while' y muestra el valor definitivo de 'h' en la ventana de comandos
end
h
El contenido del fichero es por tanto, 
f=@(t,n) 1.4-0.04*n^2/(4+t);
h=4;
nest=aproxEulermej(f,h,0,0,60);
nest(end)
diferencia=.1;
while diferencia>10^(-4)
  h=h/2;
  nestsig=aproxEulermej(f,h,0,0,60);
  nestsig(end)
  diferencia=abs(nest(end)-nestsig(end))
  nest=nestsig;
end
h
Faltaría añadirle los comentarios iniciales que expliquen qué es lo que se calcula y los convenientes comentarios de cada línea. Cuando se ejecute se obtendrán por pantalla seis sucesivas aproximaciones de $n(60)$, las correspondientes a $h=4$, $h=2$, $h=1$, $h=.5$, $h=.25$ y $h=0.125$. La diferencia entre las dos últimas es 
 7.4239e-005
Por tanto el paso buscado es $h=0.125$.