Índice de tema

 

Enunciado

Un elemento radioactivo, $A$, se descompone en otro elemento radioactivo, $B$, que a su vez se descompone en un tercero que llamaremos $C$. La velocidad de descomposición es proporcional a la cantidad presente, siendo $k_1$ y $k_2$ las correspondientes constantes (positivas) de proporcionalidad: $$A\stackrel{k_1}\longrightarrow B\stackrel{k_2}\longrightarrow C$$ Si la cantidad inicial de $A$ es $x_0$ y no hay nada de $B$ ni de $C$,
  1. Encuentra la cantidad de $B$ y la cantidad de $C$ en función del tiempo.
  2. Escribe una función para el ordenador que represente las gráficas de las cantidades de $A$, $B$ y $C$ en una misma figura en un intervalo de tiempo; esa función tendrá como variables de entrada los valores de $x_0$, $k_1$, $k_2$ y el valor final del tiempo en que deben representarse las cantidades.

Resolución del primer apartado

Paso 1

Poner nombres a las variables y escribir las ecuaciones diferenciales:
  • $x(t)$ es la cantidad de $A$ en el momento $t$
  • $y(t)$ es la cantidad de $B$ en el momento $t$
  • $z(t)$ es la cantidad de $C$ en el momento $t$
Puesto que la descomposición de $A$ se produce proporcionalmente a la cantidad de $A$ siendo $K_1>0$ la constante de proporcionalidad, la ecuación diferencial para $x(t)$ será ... piénsalo y pulsa en 'Ver'
Ver
La ecuación diferencial para $x(t)$ es $$\frac{dx}{dt}=-k_1x$$ donde el signo menos se debe a que la tasa de cambio debe ser negativa, pues el elemento se está descomponiendo.
De igual modo, la ecuación diferencial correspondiente a $y(t)$ es
$\frac{dy}{dt}=-k_2y$
$\frac{dy}{dt}=k_1x$
$\frac{dy}{dt}=(k_1-k_2)x$
Ninguna de las propuestas es correcta.
$-k_2y$ es la tasa de descomposición de $y$, pero también hay que tener en cuenta la tasa de formación de $y$
$k_1x$ es la tasa de formación de $y$, pero también hay que tener en cuenta la tasa de descomposición de $y$
No es correcto. La constante $k_2$ no debe actuar sobre la cantidad de $A$.
En efecto ninguna de las propuestas es correcta. La tasa de cambio de $y$ respecto del tiempo es la diferencia entre la tasa de formación menos la tasa de descomposición. Por tanto, $$\frac{dy}{dt}=k_1x-k_2y$$ En el caso de la cantidad $C$, no hay descomposición, sólo formación, así que $$\frac{dz}{dt}=k_2y$$

Paso 2

Encontrar $x(t)$ resolviendo la primera ecuación diferencial y teniendo en cuenta que $x(0)=x_0$: $$\frac{dx}{dt}=-k_1x \hspace{1cm} , \hspace{1cm} x(0)=x_0$$ Se trata de una ecuación separable. Encuentra su solución general y después aplica la condición para encontrar la particular. Pulsa en 'Ver' cuando lo tengas.
Ver
La solución general es $x(t)=Ce^{-k_1t}$ y la particular es $$x(t)=x_0e^{-k_1t}$$

Paso 3

Resolver la ecuación difrencial para $y(t)$, teniendo en cuenta que $y(0)=0$: $$\frac{dy}{dt}=k_1x -k_2y\hspace{1cm} , \hspace{1cm} y(0)=0$$ Pero ya $x(t)$ está determinada en el apartado anterior, así que debe buscarse la solución del problema de valor inicial: $$\frac{dy}{dt}+k_2y=k_1x_0e^{-k_1t} \hspace{1cm} , \hspace{1cm} y(0)=0$$ Se trata de una ecuación lineal, que podemos resolver mediante un factor integrante. En este caso, podemos tomar como factor integrante $\mu(t)=e^{k_2t}$; al multiplicar por él a los dos miembros de la ecuación resulta $$\frac{d}{dt}(e^{k_2t}y)=k_1x_0e^{(k_2-k_1)t}$$ de donde $$y=e^{-k_2t}k_1x_0\int e^{(k_2-k_1)t}\, dt$$ Aquí debemos separar dos casos, según que $k_1$ y $k_2$ sean distintos o sean iguales.
  • CASO $k_1\neq k_2$:
Halla la primitiva presente en la última expresión y aplica la condición inicial para encontrar $y(t)$:
$y(t)$ no existe porque debería ocurrir que $k_1x_0/(k_2-k_1))$ fuera cero y no puede serlo.
$y(t)$ sí existe.
¿Has puesto la constante de integración?
En efecto, sí existe una solución particular para ese problema. La solución general es $$y(t)=\frac{k_1x_0}{k_2-k_1}e^{-k_1t}+Ce^{-k_2t}$$ y la particular para $y(0)=0$ es $$y(t)=\frac{k_1x_0}{k_2-k_1}(e^{-k_1t}-e^{-k_2t})$$
  • CASO $k_1=k_2$:
En este caso la expresión $$y=e^{-k_2t}k_1x_0\int e^{(k_2-k_1)t}\, dt$$ se convierte en $$y=e^{-k_1t}k_1x_0\int dt$$ Halla la solución particular para la condición $y(0)=0$ y pulsa en 'Ver'.
Ver
La solución en este caso es $$y(t)=k_1x_0te^{-k_1t}$$

Paso 4

Encontrar la expresión de $z(t)$ como la solución particular del problema de valor inicial siguiente $$\frac{dz}{dt}=k_2y \hspace{1cm} ,\hspace{1cm} z(0)=0$$ o bien $$z=k_2\int y(t)\, dt \hspace{1cm} ,\hspace{1cm} z(0)=0$$ Obviamente debemos resolver por separado de nuevo los dos casos según que las constantes $k_1$ y $k_2$ sean distintas o iguales.
  • CASO $k_1\neq k_2$:
En este caso, $$z=\frac{k_1k_2x_0}{k_2-k_1}\int (e^{-k_1t}-e^{-k_2t})\, dt \hspace{1cm} ,\hspace{1cm} z(0)=0$$ Encuentra la primitiva y aplica la condición; pulsa en 'Ver' cuando tengas $z(t)$.
Ver
La solución para $k_1\neq k_2$ es $$z(t)=\frac{x_0}{k_2-k_1}[k_2(1-e^{-k_1t})+k_1(e^{-k_2t}-1)]$$
  • CASO $k_1= k_2$:
Sabemos que en este supuesto $y(t)=k_1x_0te^{-k_1t}$, luego $z(t)$ será ... encuentra la solución particular para $z(t)$ y pulsa en 'Continuar'.
Realizando la integral de $te^{-k_1t}$ por partes, tendremos que $$z=-x_0(k_1t+1)e^{-k_1t}+C$$ y aplicando la condición inicial $z(0)=0$, $$z(t)=x_0(1-(k_1t+1)e^{-k_1t})$$

Resolución del segundo apartado

En este apartado debes elaborar una función para el ordenador que dibuje las gráficas de las cantidades de $A$, $B$ y $C$ para un intervalo de tiempo que comienza en $t=0$ y termina en un valor variable. Las otras variables de la función son $x_0$ (cantidad inicial de $A$), $k_1$ y $k_2$. Iremos elaborando esta función por fases. En cada una de ellas debes pensar lo que se propone y pulsar en 'Continuar' cuando lo tengas.
  • define una función llamada 'dosreacciones', con sus variables de entrada; recuerda que el fichero .m donde escribas esta función debe llamarse dosreacciones.m:
function dosreacciones(x0,k1,k2,tf) % declaración de la función y sus variables de entrada
  • define un vector de dimensión 50 desde $t=0$ hasta $t=tf$:
t=linspace(0,tf,50);  % vector con los valores del tiempo
  • genera un vector, $x$, con las cantidades de $A$ correspondientes a esos tiempos:
x=x0*exp(-k1*t); % cantidades de A
  • Para definir los vectores $y$ y $z$ con las respectivas cantidades de $B$ y $C$ deben separarse los casos, utilizando por ejemplo un bloque if, según que $k_1$ y $k_2$ sean iguales o no:
if k1==k2
    y=k1*x0*t.*exp(-k1*t); % cantidades de B
    z=x0*(1-(1+k1*t).*exp(-k1*t)); % cantidades de C
else
    y=k1*x0*(exp(-k1*t)-exp(-k2*t))/(k2-k1); % cantidades de B
    z=x0*(k2*(1-exp(-k1*t))+k1*(exp(-k2*t)-1))/(k2-k1); % cantidades de C
end
  • Utiliza el comando 'plot' para representar los vectores $x$, $y$ y $z$ en una misma figura utilizando tres colores diferentes; añade la correspondientes leyenda y los nombres de los ejes ('Tiempo' y 'Cantidades')
plot(t,x,t,y,t,z)
legend('x(t): cantidad de elemento A','y(t): cantidad  de elemento B','z(t): cantidad  de elemento C')
xlabel('Tiempo');ylabel('Cantidades')
  • Termina la función con el correspondiente 'end'; también es aconsejable añadir algunas líneas de comentario tras la definición de la función, explicando lo que realiza y el significado de las variables de entrada.
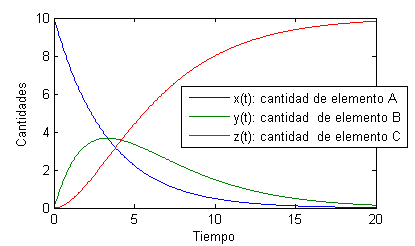
end
Una vez terminada la función, la probaremos con distintos valores de entrada. Por ejemplo, empezando con un caso en que la constante de descomposición de $A$ en $B$ sea mayor que la de $B$ en $C$, escribimos en la ventada de comandos: 
 dosreacciones(10,.3,.1,20)
obtenemos la figura

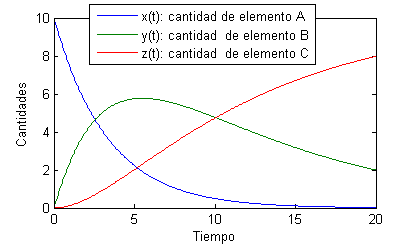
Gráfica

Por el contrario, si la constante de descomposición de $A$ en $B$ es menor que la de $B$ en $C$, 
 dosreacciones(10,.1,.3,20)
Las cantidades en este caso son

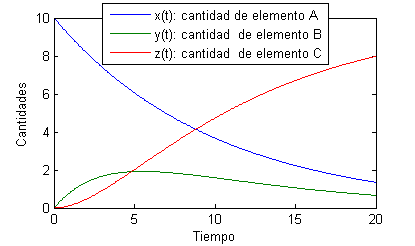
Gráfica

Por último, pongamos un ejemplo en que las constantes de descomposición sean iguales: 
 dosreacciones(10,.3,.3,20)
Observamos cómo en este caso las cantidades de $A$ y de $B$ se igualan precisamente en el máximo de $B$:

Gráfica