Índice de tema

 

Enunciado

Encuentra la forma que debe tener un espejo para que todos los rayos que partan de un punto dado se reflejen en el espejo siguiendo la misma dirección, es decir, todos los rayos reflejados tengan la misma dirección independientemente de cuál sea el punto del espejo donde hubieran incidido.

Resolución

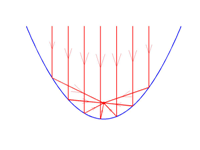
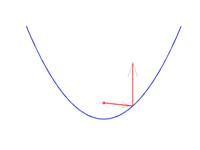
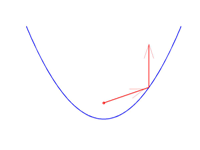
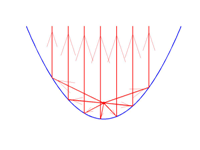
Colocando el espejo adecuadamente siempre podemos hacer que la dirección de salida de los rayos sea la vertical, es decir, formando $\pi/2$ con la horizontal. En la siguiente figura vemos seis ejemplos de cómo para cada rayo incidente, el reflejado correspondiente toma siempre la dirección vertical:
Gráfica Gráfica Gráfica
Gráfica Gráfica Gráfica
Si la forma de este espejo viene dada por la gráfica de la función $y=y(x)$, para hallarla
  1. buscaremos la ecuación diferencial ordinaria que ha de satisfacer $y=y(x)$
  2. resolveremos esa ecuación

Paso 1

Para buscar un modelo diferencial de este problema, hemos de escribir en términos de $y(x)$ y de su derivada el hecho de que la dirección del rayo reflejado sea independiente del ángulo que forma el rayo incidente con la horizontal. Para ello utilizaremos que
  • el ángulo que forman el rayo incidente y la normal es el mismo que forma el reflejado y la normal (esta es una de las leyes de la reflexión)
  • la derivada de $y(x)$ es la pendiente de la recta tangente.

Paso 1.1

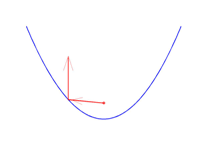
Escribir la ley de la reflexión anterior y su consecuencia en este problema en términos de ángulos: Nos situamos en un punto cualquiera de la curva, sea $(x_0,y_0)$ y trazamos un segmento de la recta tangente a $y=y(x)$ en ese punto y un segmento de la normal: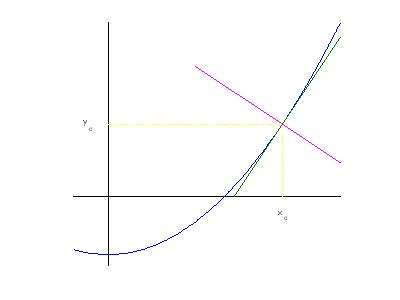

Gráfica

Dibujamos ahora un rayo que incide en el punto $(x_0,y_0)$ y marcamos el ángulo que forma con la normal; dibujamos también el reflejado y marcamos el ángulo que forma con la normal: esos ángulos son el mismo.

Gráfica

Pero puesto que vamos a introducir derivadas, nos conviene más trabajar con la tangente. ¿En qué se traduce la ley de los ángulos recién mencionada cuando se habla de la recta tangente? Piensa, dibújalo y pulsa en 'Ver'.
Ver
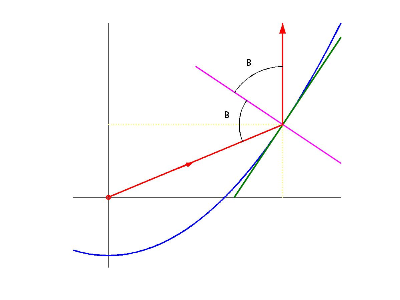
Pues obviamente con la recta tangente también se cumplirá la igualdad de ángulos del incidente y del reflejado:

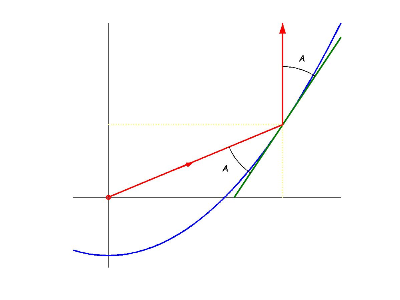
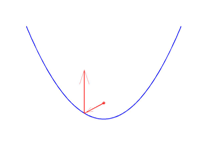
Gráfica

Pongamos ahora nombre a otros ángulos:
  • $\alpha_r$ es el ángulo que forma el rayo incidente con el eje horizontal positivo
  • $\alpha_0$ es el ángulo que forma la recta tangente con el eje horizontal positivo

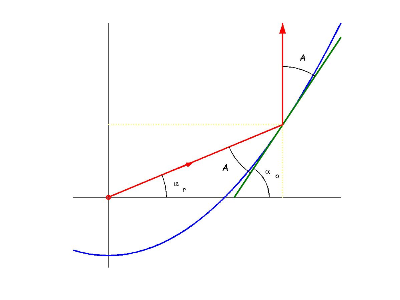
Gráfica

Piensa ahora qué relación deben cumplir los ángulos $A$, $\alpha_0$ y $\alpha_r$ y qué relación deben satisfacer los ángulos $A$ y $\alpha_0$; pulsa en 'Ver' cuando tengas las dos relaciones.
Ver
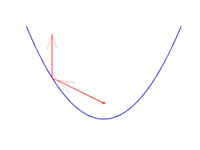
Observando en la figura superior el triángulo que forman el rayo incidente, la tangente y el eje horizontal, sabemos que $$A+\alpha_r=\alpha_0$$ Por otro lado, tomando la parte de la tangente por encima del punto $(x_0,y_0)$ (ver siguiente figura),

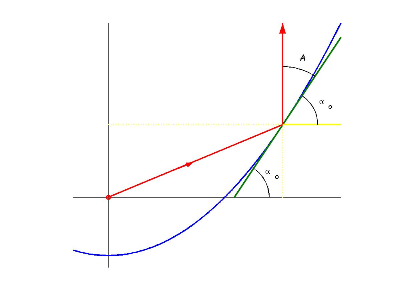
Gráfica

sabemos que $$A+\alpha_0=\frac{\pi}{2}$$ Utiliza estas dos ecuaciones para obtener la relación entre $\alpha_r$ y $\alpha_0$. Pulsa en 'Continuar' cuando lo tengas.
Tenemos la relación $$2\alpha_0=\alpha_r+\frac{\pi}{2}$$ que conduce a $$\mbox{tg}(2\alpha_0)=\mbox{tg}(\alpha_r+\frac{\pi}{2})$$

Paso 1.2

De la relación entre ángulos pasaremos a la relación entre sus tangentes: hemos tomado estos dos ángulos porque de ambos podemos fácilmente expresar sus tangentes trigonométricas. Pero antes hemos de escribir $\mbox{tg}(2\alpha_0)$ en función de la $\mbox{tg}\, \alpha_0$ y expresar $\mbox{tg}(\alpha_r+\frac{\pi}{2})$ en función de la $\mbox{tg}\, \alpha_r$. Encuentra esas dos relaciones y pulsa en 'Ver'.
Ver
Por trigonometría básica sabemos que $$\mbox{tg}(2\alpha_0)=\frac{2\,\mbox{tg}\, \alpha_0}{1-\mbox{tg}^2\, \alpha_0}$$ y $$\mbox{tg}(\alpha_r+\frac{\pi}{2})=\frac{-1}{\mbox{tg}\, \alpha_r}$$ por lo cual se cumplirá que $$\frac{2\,\mbox{tg}\, \alpha_0}{1-\mbox{tg}^2\, \alpha_0}=\frac{-1}{\mbox{tg}\, \alpha_r}$$

Paso 1.3

Debemos escribir la expresión anterior en términos de las coordenadas $x_0$ e $y_0$. Recordando cuáles eran $\alpha_r$ y $\alpha_0$,

Gráfica

sabemos que
$\mbox{tg}\, \alpha_r=\frac{x_0}{y_0}$ y $\mbox{tg}\, \alpha_0=y'(x)$
$\mbox{tg}\, \alpha_r=\frac{x_0}{y_0}$ y $\mbox{tg}\, \alpha_0=y'(x_0)$
Ninguna de las propuestas contiene las dos correctas.
$\mbox{tg}\, \alpha_r=\frac{y_0}{x_0}$ y $\mbox{tg}\, \alpha_0=y'(x_0)$
Las dos están mal.
La primera no es correcta.
Sí hay una propuesta con las dos tangentes correctas.
En efecto, esas son las tangentes. Sustituyendo en la expresión que las relacionaba entre sí, $$\frac{2\,\mbox{tg}\, \alpha_0}{1-\mbox{tg}^2\, \alpha_0}=\frac{-1}{\mbox{tg}\, \alpha_r} \hspace{1cm}\Rightarrow\hspace{1cm} \frac{2\,y'(x_0)}{1-y'(x_0)^2}=\frac{-x_0}{y_0}$$ Puesto que esto ocurre para cualquier punto $(x_0,y_0)$, la función $y=y(x)$ cumple la ecuación diferencial $$\frac{2\,y'(x)}{1-y'(x)^2}=\frac{-x}{y}$$

Paso 2

Resolución de la ecuación diferencial. Se trata de una ecuación de primer orden. Escribiéndola en la forma $$(y')^2-2\frac{y}{x}y'-1=0$$ podemos utilizar la fórmula cuadrática para llegar a $$y'=\frac{y}{x}\pm \sqrt{\frac{y^2}{x^2}+1}$$ que son dos ecuaciones que resolveremos en paralelo. Observamos que responden a la forma $y'=f(\frac{y}{x})$, lo que significa que son homogéneas . Por tanto las resolveremos con el cambio de variable $$\frac{y}{x}=t$$ Busca la ecuación equivalente para la variable $t$ y pulsa en 'Ver'.
Ver
Tras el cambio de variable, las ecuaciones son $$\frac{dt}{\pm \sqrt{t^2+1}}=\frac{dx}{x}$$
Integrando cada término, tendremos
$$\pm \log(t+\sqrt{t^2+1})=\log x$$
La propuesta no es correcta.
No es correcto, le falta algo imprescindible
En efecto, la otra expresión no es correcta pues le falta algo imprescindible.
La solución evidentemente cumple $$\pm \log(t+\sqrt{t^2+1})=\log x+K$$ Deshaciendo el cambio $t=\frac{y}{x}$ y operando un poco llegaremos a $$y=\frac{C}{2}x^2-\frac{1}{2C}$$ para $C$ cualquier real no nulo. Esta es una familia de parábolas de eje vertical, con el foco en el punto $(0,0)$ y el vértice en el punto $(0,-1/(2C))$. En la siguiente figura puedes ver una muestra de seis curvas de esta familia

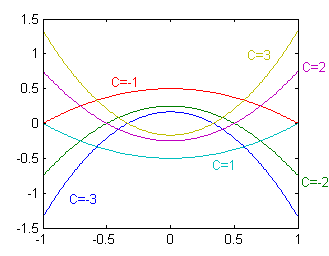
Gráfica

Se han dibujado con el código siguiente 
x=-1:.01:1;
c=[-3:-1,1:3];
[X,C]=meshgrid(x,c);
Y=C.*X.^2/2-1./(2*C);
plot(x,Y)
Ejemplos de este tipo de lentes parabólicas son
  • un reflector de rastreo, en el que la luz procedente de una fuente situada en el foco de la parábola se refleja formando un haz de luz paralelo al eje de ésta.

    Gráfica

  • un telescopio de reflexión, en el que un haz de luz paralelo al eje de la parábola se refleja por la lente parabólica de manera que todos los rayos pasan por el foco.

    Gráfica