La integral del campo ${\bf{F}}$ sobre la curva $C$ es la integral del campo
escalar : $$\int\limits_C {{\bf{F}} \cdot d{\bf{r}}} $$
donde
los elementos que intervienen:
- La curva orientada $C$: tomaremos ${\bf{r}}(t) = (x(t),y(t),z(t))$, curva suave ( $x'{(t)^2} + y'{(t)^2} + z'{(t)^2} \ne 0$ para todo $t \in [a,b]$), que comienza en $A(x(a),y(a),z(a))$ y termina en $B(x(b),y(b),z(b))$. En cada punto de la curva se definen el vector tangente unitario ${\bf{T}}(t)$ y el vector normal unitario ${\bf{n}}(t)$.
-
El campo vectorial ${\bf{F}}(x,y,z)$ definido y continuo sobre $C$. El vector ${\bf{F}}$ en cada punto de la curva tiene dos componentes:
${\bf{F}} \cdot {\bf{T}} = $ componente tangencial a la curva
${\bf{F}} \cdot {\bf{n}} = $ componente normal a la curva
Otras expresiones de la integral de línea:
- Si $C$ viene dada por la ecuación vectorial
${\bf{r}}(t)$ con $t \in \left[ {a,b} \right]$, se puede
expresar
$$\int\limits_C {{\bf{F}} \cdot d{\bf{r}}} =
\int\limits_a^b {{\bf{F}}\left( {{\bf{r}}(t)}
\right){\bf{r'}}(t)dt} = \int\limits_a^b {{\bf{F}}\left(
{{\bf{r}}(t)} \right){\bf{T}}(t)\left| {{\bf{r'}}(t)}
\right|dt = } \int\limits_C {{\bf{F}} \cdot {\bf{T}}\,ds} $$
- Tomando ${\bf{F}} = (M,N,P)$ y $d{\bf{r}} = (dx,\,\,dy,\,\,dz)$ y haciendo el producto escalar de estos dos vectores se obtiene la forma diferencial de la integral de línea $$\int\limits_C {{\bf{F}} \cdot d{\bf{r}}} = \int\limits_C {Mdx + Ndy + Pdz} $$
Interpretación física: Trabajo
Si ${\bf{F}}$ es un campo de fuerzas en el espacio, entonces una partícula que se mueva a lo largo de una curva mientras actúa sobre ella ${\bf{F}}$, realizará un trabajo W. Para calcular este trabajo se hace una partición de la curva $C$ y se calcula el trabajo parcial realizado por ${\bf{F}}$ para mover una partícula sobre un subarco cualquiera de la partición. El trabajo total será la suma de los trabajos sobre todos los subarcos considerados en $C$.
En la figura se ilustran los elementos que intervienen en este cálculo.
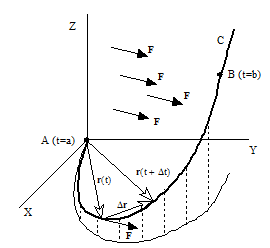
$$\Delta {\bf{r}} = {\bf{r}}(t + \Delta t) - {\bf{r}}(t)$$
con lo que es posible calcular el trabajo para ir de ${\bf{r}}(t)$ a ${\bf{r}}(t + \Delta t)$ por
$$\Delta w = {\bf{F}}\left( {{\bf{r}}(t)} \right) \cdot \Delta {\bf{r}}$$
Si subdividimos el arco AB o curva $C$ en $n$ partes iguales (partición con n subarcos), entonces el trabajo realizado por ${\bf{F}}$ se puede aproximar por la suma de Riemann
$$W \approx \sum\limits_{k = 1}^n {{\bf{F}}\left( {{\bf{r}}({c_k})} \right) \cdot \Delta {\bf{r}}} \,\,\,\,\,\,\,con\,\,\,c_k^{} \in \left[ {{t_{k - 1}},\,{t_k}} \right]$$
Cuando $\left\| C \right\| \to 0$, $\left( {n \to \infty } \right)$, esta aproximación coincide con el trabajo real realizado por ${\bf{F}}$ al recorrer la trayectoria $C$, siendo
$$W = \mathop {\lim }\limits_{\scriptstyle \left\| C \right\| \to 0 \atop
\scriptstyle (n \to \infty ) } \sum\limits_{k = 1}^n {{\bf{F}}\left( {{\bf{r}}({c_k})} \right)\Delta {\bf{r}}} = \int\limits_C {{\bf{F}} \cdot d{\bf{r}}} $$
Algunas aplicaciones
- Trabajo. Ya hemos visto que el trabajo realizado por el campo de fuerzas ${\bf{F}}$ para desplazar una partícula de masa unidad a lo largo de la curva es la integral de la componente tangencial del campo, ${\bf{F}} \cdot {\bf{T}}$, sobre la curva, puesto que sólo realiza trabajo la componente tangencial a la curva: $${\kern 1pt} Trabajo{\kern 1pt} = \int_C {\bf{F}} \cdot {\bf{T}}{\kern 1pt} ds$$
- Circulación.- Se llama así a la cantidad total de fluido que rodea una curva cerrada $C$; se calcula con la integral de línea del campo de velocidades, ${\bf{V}}$, del fluido a lo largo de la curva: $${\kern 1pt} Circulaci\acute{o} n{\kern 1pt} = \oint_C {\bf{V}} \cdot {\bf{T}}{\kern 1pt} ds$$
- Flujo.- Para calcular la cantidad de fluido, sujeto al campo
de velocidades ${\bf{V}}$, que atraviesa un elemento unidimensional (un
alambre, por ejemplo), se integrará la componente de
${\bf{V}}$ normal a
la curva que dibuja el alambre, es decir: $${\kern 1pt}
Flujo{\kern 1pt} = \int_C {\bf{V}} \cdot {\bf{n}}{\kern
1pt} ds$$
