TEOREMA DE GREEN EN EL PLANO.-
Hipótesis: los elementos que intervienen en este teorema son
- la curva $C$ que es cerrada, simple, suave por partes y orientada positivamente
- la región $D$ del plano encerrada por la curva $C$
- un campo vectorial ${\bf{F}}(x,y) = (M(x,y),N(x,y))$ de clase $C^1$ sobre y
Tesis: bajo estas hipótesis se verifica que
$$\oint_C M{\kern 1pt} dx + N{\kern 1pt} dy = \int \int_D \left( {{{N'}_x} - {{M'}_y}} \right){\kern 1pt} dA$$
OBSERVACION.- Teniendo en cuenta que el vector tangente y un vector normal unitario a la curva en cada punto son, respectivamente: $${\bf{T}} = {{{{dx} \over {dt}}{\bf{i}} + {{dy} \over {dt}}{\bf{j}}} \over {\sqrt {{{\left( {{{dx} \over {dt}}} \right)}^2} + {{\left( {{{dy} \over {dt}}} \right)}^2}} }} \,\,\,\,\,\,\, {\bf{n}} = \pm {{{{dy} \over {dt}}{\bf{i}} - {{dx} \over {dt}}{\bf{j}}} \over {\sqrt {{{\left( {{{dx} \over {dt}}} \right)}^2} + {{\left( {{{dy} \over {dt}}} \right)}^2}} }}$$ pueden obtenerse las siguientes expresiones de la tesis del teorema de Green
i) $\oint\limits_C {{\bf{F}} \cdot {\bf{T}}ds} = \int\!\!\!\int\limits_D {({\mathop{\rm rot}\nolimits} {\bf{F}}){\bf{k}}\,dA} $
ii) $\oint\limits_C {{\bf{F}} \cdot {\bf{n}}ds} = \int\!\!\!\int\limits_D {{\mathop{\rm div}\nolimits} {\bf{F}}\,dA} $
Estas expresiones constituyen, respectivamente, la tesis del teorema de Stokes en el plano y del teorema de la divergencia de Gauss en el plano.
Aplicación del Teorema de Green al cálculo de un área plana
El teorema de Green que hemos enunciado se ha establecido para una curva suave C que forma la frontera de la región D del plano. ¿Qué ocurre si la frontera de la región D no es una única curva, sino la unión de varias? ¿Cómo se generaliza el teorema de Green a este tipo de regiones?
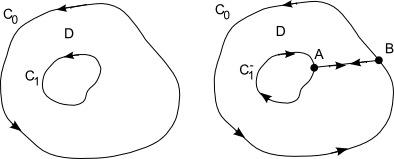
TEOREMA DE GREEN GENERALIZADO.- Sean ${C_0}$ y ${C_1}$ dos curvas simples cerradas orientadas positivamente, suaves por partes tales que no se cortan, estando ${C_1}$ encerrada por ${C_0}$ . Sea D la región anular entre ${C_0}$ y ${C_1}$ . Si M y N son funciones de clase $C^1$ en un abierto que contiene a D, entonces $$\int\!\!\!\int\limits_D {\left( {{{\partial N} \over {\partial x}} - {{\partial M} \over {\partial y}}} \right)dA} = \oint\limits_{{C_0}} {\left( {Mdx + Ndy} \right)} - \oint\limits_{{C_1}} {\left( {Mdx + Ndy} \right)} $$