Integral de un campo escalar sobre una curva

 

 

La integral de línea de un campo escalar en $R^2$ se representa por $\int_C f(x,y){\kern 1pt} ds$ siendo:

La integral de línea de un campo escalar en $R^3$ se representa por $\int_C f(x,y,z){\kern 1pt} ds$ siendo:

 

Definición (Diferencial de arco).- Dada una curva C, se llama diferencial de arco a la longitud del arco elemental, que se define como $ds = \sqrt {d{x^2} + d{y^2}} $, en ${R^2}$ y como $ds = \sqrt {d{x^2} + d{y^2} + d{z^2}} $, en ${R^3}$.

Dependiendo de la ecuación de la curva, esta diferencial y la integral de línea toma distintas expresiones.

Curva en cartesianas

Curva plana:

Para la curva C dada por $y = \varphi (x)  con \quad x \in \left[ {a,b} \right] $, continua con derivada continua, se busca una aproximación ($\Delta s$ en la figura) para la longitud del arco correspondiente a un cambio ($\Delta x$ en la figura) en la variable x.

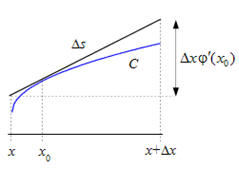
diferencial arco cartesianas

Para ello tomamos un punto ${x_0}$ cualquiera entre $x$ y $x + \Delta x$ y trazamos por él la tangente a la curva. La longitud del segmento de tangente que se proyecta sobre $[x,x + \Delta x]$ es $\Delta s$ y cuando $\Delta x$ tiende a cero, $\Delta s$ tiende a $ds$.
$$\Delta s = \sqrt {1 + \varphi '{{({x_0})}^2}} \Delta x$$ $$\quad ds = \mathop {\lim }\limits_{\Delta x \to 0} \Delta s = \sqrt {1 + \varphi '{{(x)}^2}} dx$$
En este caso la integral de línea de la función $f(x,y)$ sobre C es, $$\int\limits_C {f(x,y)ds} = \int\limits_a^b {f(x,\varphi (x))\sqrt {1 + \varphi '{{(x)}^2}\,} } dx$$

Curva en el espacio:

En el caso de que la curva C venga dada como intersección de dos superficies se deberá parametrizar la curva como se indica en el siguiente apartado.

Curva en paramétricas

  • En ${R^2} $: ${\bf{r}}(t) = (x(t),y(t)) ,\,\,\, t \in \left[ a, b \right]$ , con $x(t)$ e $y(t)$ y derivables con derivada continua. El elemento diferencial de arco es, $$ds = \sqrt {x'{{(t)}^2} + y'{{(t)}^2}} dt = |r'(t)|dt$$ y la integral de línea de $f$ sobre $C$ es$$\int_C f(x,y){\kern 1pt} ds = \int_a^b f(x(t),y(t))\sqrt {x'{{(t)}^2} + y'{{(t)}^2}} {\kern 1pt} dt$$
  • En ${R^3}$ : ${\bf{r}}(t) = (x(t),y(t),z(t)) ,\,\,\, t \in \left[ a, b \right]$ , con $x(t)$, $y(t)$ y $z(t)$ derivables con derivada continua. El elemento diferencial de arco es, $$ds = \sqrt {x'{{(t)}^2} + y'{{(t)}^2} + z'{{(t)}^2}} dt = |r'(t)|dt$$La integral de línea $f$ sobre $C$ es,  $$\int_C f(x,y,z){\kern 1pt} ds = \int_a^b f(x(t),y(t),z(t))\sqrt {x'{{(t)}^2} + y'{{(t)}^2} + z'{{(t)}^2}} {\kern 1pt} dt$$En el caso de que la curva C venga dada como intersección de dos superficies $$\left\{ \matrix{
    F(x,y,z) = 0 \cr
    G(x,y,z) = 0  \cr} \right.$$ se intentará parametrizar la curva. Esto siempre se puede hacer eligiendo una variable independiente entre $x,\,\,y,\,\,z$ y poniendo las otras dos variables en función de la elegida, utilizando las ecuaciones de las superficies. Supongamos que se ha elegido la variable $x$ como independiente. De las ecuaciones de las superficies despejaríamos $y = y(x),\,\,z = z(x)$, que sustituidas en la integral de línea conducirían a una integral en la variable $x$:
    $$\int\limits_C {f(x,y,z)ds} = \int\limits_{{x_0}}^{{x_1}} {f\left( {x,y(x),z(x)} \right)\sqrt {1 + y'{{(x)}^2} + z'{{(x)}^2}} \,dx} $$

Curva plana en polares

La curva en polares $r = r(\theta ),\,\,\,\theta \in \left[ {{\theta _0},{\theta _1}} \right]$ , con $r$ una función continua con derivada continua se puede expresar por las ecuaciones paramétricas $$x(\theta ) = r(\theta ){\kern 1pt} \cos \theta \;\;,\;\;y(\theta ) = r(\theta ){\kern 1pt} {\kern 1pt} {\mathop{\rm sen}\nolimits} {\kern 1pt} {\kern 1pt} \theta ,\,\,\,\theta \in \left[ {{\theta _0},{\theta _1}} \right]$$ Aplicando la definición del diferencial de arco para una curva en paramétricas y simplificando, se obtiene que para este caso $$ds = \sqrt {r{{(\theta )}^2} + r'{{(\theta )}^2}} {\kern 1pt} d\theta $$

La integral de línea de $f$ sobre $C$ es, $$\int\limits_C {f(x,y)ds} = \int\limits_{{\theta _0}}^{{\theta _1}} {f(r(\theta )\cos \theta ,r(\theta ){\mathop{\rm sen}\nolimits} \theta )\sqrt {r{{(\theta )}^2} + r'{{(\theta )}^2}\,} } d\theta $$