Si se consideran una curva plana $C$ y la función continua $z = f(x,y)$ y no negativa sobre $C$, entonces la integral de sobre $C$ representa el área de la valla o cortina vertical apoyada sobre $C$ y cuya altura en cada punto viene dada por $ f(x,y)$.

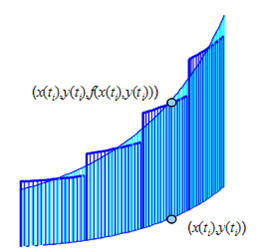
Figura.- Interpretación de la integral de un campo escalar sobre una curva.

JUSTIFICACIÓN

Sean $x = x(t),\,\,\,y = y(t)$ con unas ecuaciones paramétricas de C. Se divide el intervalo $[a,b]$ en $n$ intervalos (partición de $\left[ {a,b} \right]$), lo que también divide el arco en $n$ pequeños subarcos (partición de $C$). Sobre cada subarco $k$ se toman las siguientes aproximaciones :

• $\Delta {s_k}$ como la longitud del subarco
• el valor de $f$ en cualquier punto $\left( {{x_k},{y_k}} \right)$ del subarco.

Con esto, la suma de Riemann de $f$ sobre $C$
$$\sum\limits_{k = 1}^n f({x_k},{y_k}){\kern 1pt} \Delta {s_k}$$
aproxima el área de la valla vertical apoyada sobre C, y su límite cuando $\left\| C \right\| \to 0$, tiende a la integral de línea cuyo valor será precisamente el área de dicha valla.
$$\acute{A}rea = \mathop {\lim }\limits_{\scriptstyle \left\| C \right\| \to 0 l \atop
\scriptstyle (n \to \infty ) } \sum\limits_{k = 1}^n {f({x_k},{y_k})\Delta {s_k}} = \int\limits_C {f(x,y)ds} $$

PROPIEDAD P1 (Linealidad).- La integral de una combinación lineal de funciones es la combinación lineal de las integrales.

PROPIEDAD P2 (Aditividad de la curva de integración).- La integral sobre una curva que sea unión de varias es la suma de las integrales sobre cada una de ellas; por ejemplo, para la unión de dos curvas:
$$\int_{{C_1} \cup {C_2}} f(x,y,z){\kern 1pt} ds = \int_{{C_1}} f(x,y,z){\kern 1pt} ds + \int_{{C_2}} f(x,y,z){\kern 1pt} ds$$

PROPIEDAD P3 (Independencia de la parametrización).- El valor de la integral no cambia con la parametrización elegida para la curva.

PROPIEDAD P4 (Independencia de la orientación).- El signo de la integral no cambia con la orientación fijada en la curva.