Índice de tema

 

Enunciado

Sea $${\bf V}=(x+y^2,-x)$$ el campo de velocidades de un fluido y $C$ la circunferencia de radio $R$ centrada en el origen, orientada en sentido positivo.
  1. Calcula el flujo saliente de fluido a través de $C$.
  2. Prepara una función para el ordenador que tome como variable de entrada el radio $R$ y un número $m$. El valor de $m$ es el número de puntos que se tomarán, igualmente espaciados, sobre $C$ para situar en ellos el vector ${\bf V}$ correspondiente; la función debe también dibujar la curva y los vectores normales a ella en esos mismos puntos; tendrá como variable de salida el valor del flujo saliente.

Resolución del primer apartado

Paso 1

Saber qué integral hemos de hacer. Una de las interpretaciones de la integral de un campo vectorial sobre una curva es precisamente el cálculo del flujo que atraviesa una curva; para este cálculo, la única componente del campo vectorial que se ha de tomar es la normal a la curva: $$\mbox{flujo}=\oint_C {\bf V}\cdot {\bf n}\, ds$$ donde ${\bf n}$ es la normal unitaria, que será la que apunte hacia fuera si el flujo buscado es el saliente: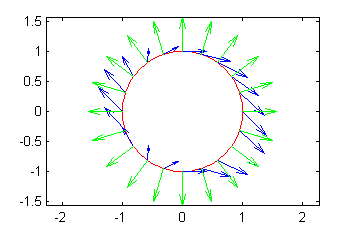
Gráfica

Paso 2

Parametrizar la curva. En este caso, la curva $C$ admite las ecuaciones paramétricas:
$x(t)=t ,\hspace{.2cm} y(t)=\sqrt{R^2-t^2}, \hspace{.3cm} t\in[-R,R]$
$x(t)=\cos t ,\hspace{.2cm} y(t)=\mbox{sen}\, t, \hspace{.3cm} t\in[0,2\pi]$
$x(t)=\mbox{sen}\, t ,\hspace{.2cm} y(t)=\cos t, \hspace{.3cm} t\in[0,2\pi]$
Hay más de una opción correcta.
$x(t)=r \cos t ,\hspace{.2cm} y(t)=r\,\mbox{sen}\, t, \hspace{.3cm} t\in[0,2\pi],\hspace{.2cm} r\in[0,R]$
$x(t)=R \cos t ,\hspace{.2cm} y(t)=R\,\mbox{sen}\, t, \hspace{.3cm} t\in[0,2\pi]$
Esa sería sólo la semicircunferencia superior.
Esa tendría radio 1. Debes dejar que el radio sea cualquiera.
Esa es la circunferencia de centro el origen y radio $R$, pero está orientada en sentido horario.
No, sólo una de las opciones es correcta.
¡No!, eso es una porción de superficie: depende de dos variables
En efecto, esa es la correcta.

Paso 3

Hallar el vector normal. Derivando cada componente de la curva respecto de $t$, hallamos las componentes del tangente: $$x'(t)=-R \,\mbox{sen}\, t ,\hspace{.2cm} y'(t)=R\cos t$$ Por tanto el vector normal saliente es
${\bf N}=(\frac{1}{R\cos t},\frac{1}{-R \,\mbox{sen}\, t})$
${\bf N}=(-R\cos t,-R \,\mbox{sen}\, t )$
${\bf N}=(R\cos t,R \,\mbox{sen}\, t )$
Ese no daría producto escalar nulo con el tangente
Ese es normal, pero apunta hacia dentro de la curva
Sí, ese el normal que necesitamos. Ahora, puesto que $ds=|{\bf N}|\, dt$ y ${\bf n}=\frac{{\bf N}}{|{\bf N}|}$ $$\mbox{flujo}=\oint_C {\bf V}\cdot {\bf n}\, ds=\int_0^{2\pi} {\bf V}(x(t),y(t))\cdot {\bf N}\, dt$$

Paso 4

Evaluar el campo sobre la curva y realizar el producto escalar con la normal. Haz tú este paso y pulsa en 'Ver' cuando lo tengas.
Ver
$${\bf V}(x(t),y(t))=(R\cos t+R^2\,\mbox{sen}^2\, t,-R\cos t)$$ luego $${\bf V}(x(t),y(t))\cdot {\bf N}=(R\cos t+R^2\,\mbox{sen}^2\, t,-R\cos t)\cdot(R\cos t,R \,\mbox{sen}\, t )=$$ $$=R^2(\cos^2 t+\cos t\,\mbox{sen}^2\, t-\cos t\,\mbox{sen}\, t)$$

Paso 5

Hacer la integral simple $$\mbox{flujo}=\int_0^{2\pi} R^2(\cos^2 t+\cos t\,\mbox{sen}^2\, t-\cos t\,\mbox{sen}\, t)\, dt$$ Esta integral es suma de tres inmediatas. Hállalas y pulsa en 'Ver'.
Ver
  • $R^2\int_0^{2\pi} \cos^2 t\, dt= R^2\pi$
  • $R^2\int_0^{2\pi} \cos t\,\mbox{sen}^2\, t\, dt= \frac{1}{3}\,\mbox{sen}^3\, t]_0^{2\pi}=0$
  • $R^2\int_0^{2\pi} \cos t\,\mbox{sen}\, t\, dt= \frac{1}{2}\,\mbox{sen}^2\, t]_0^{2\pi}=0$
Por tanto, el flujo saliente es $R^2\pi$.

Resolución del segundo apartado

En un fichero llamado por ejemplo, flujocircular.m, escribiremos una función con dos variables de entrada, $R$ y $m$, que dibuja
  • la curva,
  • $m$ vectores del campo de velocidades sobre puntos de la curva,
  • $m$ vectores normales a la curva,
y devuelve el valor de flujo saliente correspondiente. Podríamos escribir esta función siguiendo los siguientes pasos (cuando hagas cada uno, pulsa en 'Continuar')
  • declara la función con sus variables de entrada y salida
function flujo=flujocircular(R,m)
  • define un vector,$t$, de parámetros entre 0 y $2\pi$ 
t=0:pi/50:2*pi; % vector de parámetros
  • define los vectores de abscisas y ordenadas de la curva para esos valores del parámetro, $x$ e $y$ 
x=R*cos(t); % primera componente del arco
y=R*sin(t); % segunda componente del arco
  • dibuja la curva en rojo y fija igual escala para ambos ejes 
plot(x,y,'r') % dibujo del arco
axis equal
  • define un vector, $tv$, con los $m$ valores del parámetro correspondientes a los puntos donde se situarán los vectores: el primer valor será el $0$ y el último será $2\pi-(2\pi/m)$, pues $0$ y $2\pi$ dan el mismo punto de la curva 
tv=linspace(0,2*pi-2*pi/m,m) ; % vector de valores del parámetro
  • dibuja en azul sobre la curva (deberás poner 'hold on' antes del 'quiver') los vectores del campo correspondientes a los valores de $tv$ 
hold on
quiver(R*cos(tv),R*sin(tv),R*cos(tv)+R^2*sin(tv).^2,-R*cos(tv)) % vectores del campo sobre la curva
  • dibuja en verde los vectores normales a la curva en los puntos correspondientes a $tv$; esto es lo último que se hará en esta figura, así que añade 'hold off' 
quiver(R*cos(tv),R*sin(tv),R*cos(tv),R*sin(tv),'g') % vectores normales
hold off
  • ya se ha terminado el dibujo, ahora pasamos a calcular el flujo; comienza declarando una variable simbólica 
syms u
  • calcula la integral entre 0 y $2\pi$ del producto escalar del campo por la normal y guárdalo en la variable de salida, $flujo$; cierra la función 
flujo=int(sum([R*cos(u)+R^2*sin(u).^2,-R*cos(u)].*[R*cos(u),R*sin(u)]),0,2*pi);
end
Faltaría añadir unas líneas de comentario explicativas de lo que hace la función; todas estas líneas juntas son 
function flujo=flujocircular(R,m)
%%%% líneas de comentario explicativas de lo que hace la función
% dibuja de la curva y los vectores
t=0:pi/50:2*pi; % vector de parámetros del arco
x=R*cos(t); % primera componente del arco
y=R*sin(t); % segunda componente del arco
plot(x,y,'r') % dibujo del arco
axis equal
tv=linspace(0,2*pi-2*pi/m,m) ; % vector de valores del parámetro
hold on
quiver(R*cos(tv),R*sin(tv),R*cos(tv)+R^2*sin(tv).^2,-R*cos(tv)) % vectores del campo sobre la curva
quiver(R*cos(tv),R*sin(tv),R*cos(tv),R*sin(tv),'g') % vectores normales
hold off
% cálculo de la integral de F sobre C
syms u
flujo=int(sum([R*cos(u)+R^2*sin(u).^2,-R*cos(u)].*[R*cos(u),R*sin(u)]),0,2*pi);
end
Ejecutando 
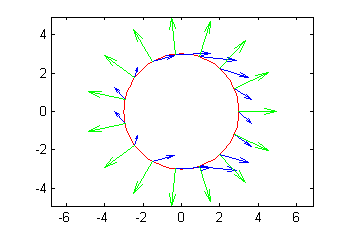
flujo=flujocircular(3,15)
en la ventana de comandos, obtenemos que el flujo para la circunferencia de radio $3$ es efectivamente $9\pi$ y la figura generada es
Gráfica