Enunciado
Tomamos la curva $C$ como el contorno del cuadrado cuyos vértices están en los puntos $A(1,0)$, $B(0,1)$, $C(-1,0)$, $D(0,-1)$ y que se recorre en sentido contrario a las agujas del reloj.
- Dibuja en el ordenador la curva $C$ y sobre ella una muestra de vectores del campo $${\bf F}(x,y)=\left(\frac{1}{x+y},\frac{-1}{x+y}\right)$$
- Calcula la integral $$I=\oint_C \frac{dx-dy}{x+y}$$
Resolución del primer apartado
- En primer lugar dibujaremos la curva C; puesto que es el contorno de un cuadrado, basta que en el plot pongamos las abscisas y las ordenadas de los vértices. Inténtalo y pulsa en 'Ver'
Ver
plot([1 0 -1 0 1],[0 1 0 -1 0])
- generar las abscisas de los puntos donde se colocarán los vectores: escogemos
$(0,1)$, $(.25,.75)$, $(.5,.5)$, $(.75,.25)$, $(1,0)$, $(.75,-.25)$, $(.25,-.75)$, $(0,-1)$, $(-.25,-.75)$, $(-.5,-.5)$, $(-.75,-.25)$, $(-1,0)$, $(-.75,.25)$ y $(-.25,.75)$
x=0:.25:1; X=[x .75 .25 -x -.75 -.25]; %abscisas de los puntos de la lista anterior
- generar las ordenadas de los puntos de la lista anterior
y=x(end:-1:1); Y=[y -.25 -.75 -y .25 .75];
- marcamos con un signo + los puntos donde colocaremos los vectores
hold on plot(X,Y,'+')
- dibujamos con quiver los vectores correspondientes a los puntos elegidos
quiver(X,Y,1./(X+Y),-1./(X+Y),'r') hold off axis equalEjecutando todas estas líneas se obtiene la siguiente figura:
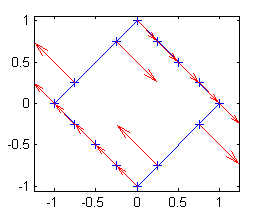
En la siguiente se han añadido las componentes de los vectores:
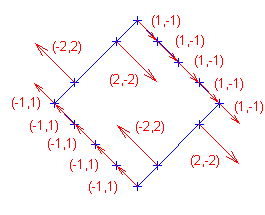
Resolución del segundo apartado
Paso 1
¿Cómo hacemos esta integral? Puesto que se trata de una curva cerrada, ¿podemos utilizar el teorema de Green ?
Sí, con $M=\frac{1}{x+y}$ y $N=\frac{-1}{x+y}$
No, no se puede aplicar Green.
¡No! no se puede aplicar ese teorema, pues $M$ y $N$ no son continuas en todo el cuadrado.
En efecto, no se puede aplicar el teorema, ya que $M$ y $N$ no cumplen la condición de continuidad en el interior de $C$. Por tanto, hemos de hallar el valor de la integral paramentrizando la curva $C$.
Paso 2
Hemos de escribir $C$ como unión de los cuatro lados del cuadrado,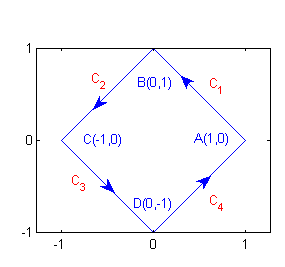
$$C=\cup_{i=1}^4 C_i$$
y calcular la integral como
$$I=\sum_{i=1}^4 \int_{C_i} \frac{dx-dy}{x+y}=\sum_{i=1}^4 I_i$$
Iremos ahora calculando cada una de las integrales $I_i$: para parametrizar $C_1$ podemos utilizar $y$ como parámetro:
$$C_1: \ \ x=1-y \ \ , \ \ y\in[0,1]$$
Calcula tú $I_1$ y pulsa en 'Ver'.
Ver
$$dx=-dy\ \ \Rightarrow \ \ \frac{dx-dy}{x+y}=-2\, dy\ \ \Rightarrow \ \ I_1=-2\int_0^1 dy=-2$$
Observa en la figura de la muestra de vectores del campo, que sobre este lado los vectores actúan en contra del movimiento.
Calcula la integral $I_2$, correspondiente al lado entre $B(0,1)$ y $C(-1,0)$, y pulsa en 'Ver'.
Ver
$$C_2: \ \ x=y-1 \ \ , \ \ y\in[0,1]\ \ \mbox{sentido opuesto} \ \ \Rightarrow \ \ dx=dy
\ \ \Rightarrow \ \ \frac{dx-dy}{x+y}=0\ \ \Rightarrow \ \ I_2=0$$
Observa que en todos los puntos de este lado, el campo es perpendicular a la trayectoria.
Halla la integral $I_3$, correspondiente al lado entre $C(-1,0)$ y $D(0,-1)$, y pulsa en 'Ver'. Puedes utilizar $x$ como parámetro.
Ver
$$C_3: \ \ y=-x-1 \ \ , \ \ x\in[-1,0]\ \ \Rightarrow \ \ dy=-dx
\ \ \Rightarrow \ \ \frac{dx-dy}{x+y}=-2\, dx\ \ \Rightarrow \ \ I_3=-2\int_{-1}^0 dx=-2$$
Observa en la figura de la muestra de vectores del campo, que sobre este lado los vectores actúan en contra del movimiento.
Calcula por último la integral $I_4$, correspondiente al lado entre $D(0,-1)$ y $A(1,0)$, y pulsa en 'Ver'. Puedes utilizar $x$ como parámetro.
Ver
$$C_4:\ \ y=x-1 \ \ , \ \ x\in[0,1]\ \ \Rightarrow \ \ dy=dx
\ \ \Rightarrow \ \ \frac{dx-dy}{x+y}=0\ \ \Rightarrow \ \ I_4=0$$
Observa que en todos los puntos de este lado, el campo es perpendicular a la trayectoria.
Una vez realizadas las cuatro integrales concluímos que
$$I=-4$$
Resumen
- Comprobar si puede utilizarse el teorema de Green;
- puesto que no, descomponer la curva en unión de curvas suaves;
- integrar en cada uno de esos segmentos:
- parametrizar
- evaluar integrando
- resolver integral de una variable.