Definiciones: Campos escalares y vectoriales
Definición (Campo escalar).- Un campo escalar es una función real que asocia a cada punto $P \in A$ un número real. $$f:\,\,A \subset {R^n} \to R$$
Definición (Campo vectorial).- Un campo vectorial en ${R^n}$ es una función $${\bf{F}}:A \subset {R^n} \to {R^n}$$ que asigna a cada punto $P \in A$ un vector ${\bf{F}}(P)$.
La imagen gráfica de un campo vectorial surge de asociar a cada punto del espacio un vector que sale de él.
En este tema trabajaremos con campos escalares y vectoriales en ${R^2}$ y en ${R^3}$ .
Si ${\bf{F}}:\,\,\,A \subset {^3} \to {^3}$ es un campo vectorial llamaremos M, N y P a sus tres componentes escalares, es decir $${\bf{F}}(x,y,z) = M(x,y,z){\bf{i}} + N(x,y,z){\bf{j}} + P(x,y,z){\bf{k}}$$
Las propiedades de un campo vectorial en cuanto a continuidad o derivabilidad se establecen a partir de las propiedades que verifican sus componentes escalares. Por ejemplo, un campo vectorial es de clase ${C^r}$ si cada una de sus componentes lo es (derivable con continuidad hasta orden ).
En este tema trabajaremos con campos escalares y vectoriales en ${R^2}$ y en ${R^3}$ .
Si ${\bf{F}}:\,\,\,A \subset {^3} \to {^3}$ es un campo vectorial llamaremos M, N y P a sus tres componentes escalares, es decir $${\bf{F}}(x,y,z) = M(x,y,z){\bf{i}} + N(x,y,z){\bf{j}} + P(x,y,z){\bf{k}}$$
Las propiedades de un campo vectorial en cuanto a continuidad o derivabilidad se establecen a partir de las propiedades que verifican sus componentes escalares. Por ejemplo, un campo vectorial es de clase ${C^r}$ si cada una de sus componentes lo es (derivable con continuidad hasta orden ).
Definición (Línea de fuerza o línea de flujo).- Es una curva ${\bf{r}}(t)$ tal que $${\bf{r}}'(t) = {\bf{F}}({\bf{r}}(t))$$ es decir,${\bf{F}}$ produce el campo de velocidades de la curva.
Geométricamente significa que el vector campo es tangente a la línea de fuerza en cada punto.
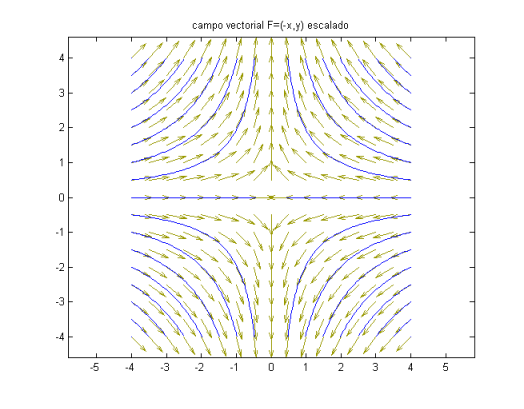
Ejemplos de campos vectoriales en ${R^3}$:
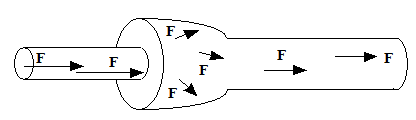
Figura 1.- Campo vectorial de velocidades del flujo en una tubería.
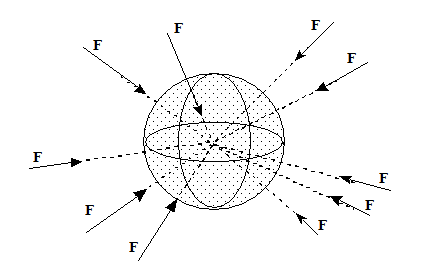
Figura 2.- Campo vectorial gravitacional de Newton
Ejercicios interactivos: