Índice de tema

 

Enunciado

Encuentra la transformada inversa de $$F(s)=\frac{(e^{-as}-e^{-bs})^2}{s^2}$$ siendo $0<a<b$. Comprueba el resultado con el ordenador y representa, para $a=1$ y $b=3$, las funciones $F(s)$ y ${\cal L}^{-1}[F]$.

Paso 1

Escribir $F(s)$ desarrollando el cuadrado: $$F(s)=\frac{1}{s^2}(e^{-2as}-2e^{-(a+b)s}+e^{-2bs})$$

Paso 2

Utilizar la propiedad de traslación en la variable $s$ para escribir $f(t)={\cal L}^{-1}[F]$ en función de $$g(t)={\cal L}^{-1}[\frac{1}{s^2}]$$ Realiza este paso y pulsa en 'Ver'.
Ver
Puesto que aparecen tres exponenciales, tendremos tres traslaciones: para $c=2a$, para $c=a+b$ y para $c=2b$: $$f(t)=g(t-2a)U(t-2a)-2g(t-(a+b))U(t-(a+b))+g(t-2b)U(t-2b)$$

Paso 3

Sustituir en la expresión anterior $g(t)$; en la tabla básica de transformadas encontramos que $$g(t)={\cal L}^{-1}[\frac{1}{s^2}]=t$$ luego $$f(t)=(t-2a)U(t-2a)-2(t-(a+b))U(t-(a+b))+(t-2b)U(t-2b)$$ ¿Cuál es la expresión por casos de esta función? Piénsalo y pulsa en 'Ver'
Ver
Puesto que $a<b$, entonces $2a< 2b$; de hecho, $a+b$ es el punto medio entre $2a$ y $2b$:
  • entre 0 y $2a$ los tres escalones $U(t-c)$ de la expresión de $f(t)$ valen cero
  • entre $2a$ y $a+b$ valen 0 todos menos $U(t-2a)$, que vale 1
  • entre $a+b$ y $2b$ valen 1 los escalones $U(t-2a)$ y $U(t-(a+b))$ y vale 0 el $U(t-2b)$
  • a partir de $2b$ todos los escalones valen 1
así que $$f(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t<2a \\ t-2a & \mbox{si} & 2a<t<a+b \\ 2b-t & \mbox{si} & a+b<t<2b \\ 0 & \mbox{si} & t >2b \end{array}\right.$$

Paso 4

Comprobación del resultado con el ordenador y representación de las funciones. Escribe en un fichero las líneas de código con las que
  1. declaras 's' como variable simbólica
  2. asignas los valores a los parámetros 'a' y a 'b'
  3. defines 'F' para que guarde la expresión de $F(s)=\frac{(e^{-as}-e^{-bs})^2}{s^2}$
  4. activas la figura 1 ('figure(1)')
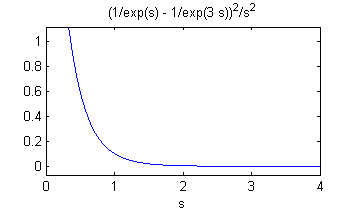
  5. dibujas con 'ezplot' la función 'F' entre 0 y 4
  6. activas la figura 2
  7. defines 'f' como la transformada inversa de 'F' (con 'ilaplace')
  8. dibujas con 'ezplot' la función 'F' entre 0 y 8
Pulsa en 'Ver' cuando lo tengas.
Ver 
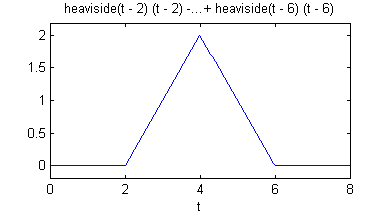
syms s
a=1;b=3;
F=(exp(-a*s)-exp(-b*s))^2/(s^2);
figure(1)
ezplot(F,[0,4])
figure(2)
f=ilaplace(F)
ezplot(f,[0,8])
Cuando ejecutemos este fichero, obtendremos en la ventana de comandos la transformada inversa: 
f =

heaviside(t - 2)*(t - 2) - 2*heaviside(t - 4)*(t - 4) + heaviside(t - 6)*(t - 6)
En la ventana 'Figure 1' tenemos la representación de $F(s)$:

Gráfica

y en la ventana 'Figure 2' la de $f(t)$:

Gráfica