Enunciado

El volumen $V$, medido en cm$^3$, de 1 mol de un gas ideal está dado por $$V=k\frac{T}{p}$$ donde $T$ es la temperatura absoluta medida en grados Kelvin (K) (recuerda que K$=^o\mbox{C}+273$) y $p$ es la presión medida en atmósferas. El valor de la constante es $k=82.06$.

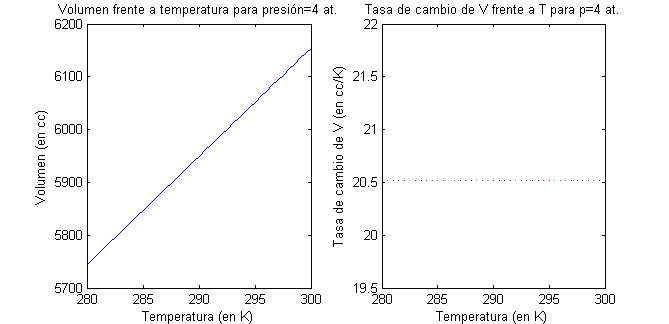
1. Halla la razón de cambio del volumen respecto de la temperatura cuando se mantiene constante la presión. Dibuja las gráficas del volumen y de la variación del volumen frente a la temperatura, en $[280,300]$, cuando $p=4$ atmósferas.
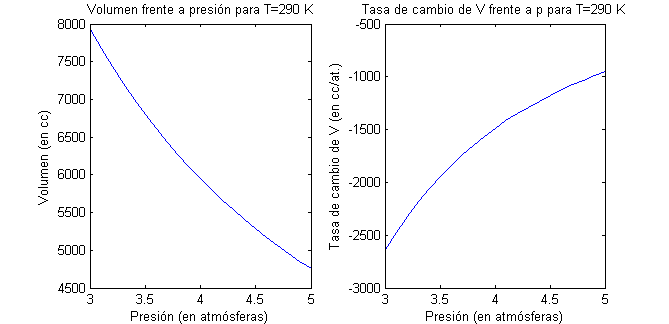
2. Halla la razón de cambio del volumen respecto de la presión cuando se mantiene constante la temperatura. Dibuja las gráficas del volumen y de la variación del volumen frente a la presión, en $[3,5]$, cuando $T=290\,$K.
3. Utilizando diferenciales estima el volumen si los errores admisibles son de media unidad en los grados Kelvin y una décima en las atmósferas, cuando se toma $T=290\,$K y $p=4$ atmósferas. (Estimar el volumen quiere decir calcularlo para esos valores de temperatura y presión y además calcular la cota de error que se ha podido producir a consecuencia de los errores en las medidas de partida)

Resolución del primer apartado

La razón de cambio del volumen respecto de la temperatura cuando se mantiene constante la presión es

la derivada parcial de $V$ respecto de $p$

la derivada parcial de $V$ respecto de $T$

No es correcto; es la presión, $p$ la que dejamos constante y la temperatura la que cambia; Elige de nuevo

En efecto, hemos de derivar $V=k\frac{T}{p}$ respecto de $T$: $$\frac{\partial V}{\partial T}(T,p)=k\frac{1}{p}$$ Para $p=4$, la función que da el volumen en función de la temperatura es $$V(T,4)=k\frac{T}{4}$$ y la variación del volumen respecto de la temperatura es $$\frac{\partial V}{\partial T}(T,4)=\frac{k}{4}=20.515$$ Podemos dibujar la gráfica del volumen frente a la temperatura cuando se mantiene la presión constantemente a 4 atmósferas y la gráfica de la variación del volumen en esas mismas circunstancias, poniendo

k=82.06;
T=280:.5:300;
V=k*T/4;
subplot(1,2,1)
plot(T,V)
title('Volumen frente a temperatura para presión=4 at.')
xlabel('Temperatura (en K)')
ylabel('Volumen (en cc)')
subplot(1,2,2)
plot(T,k/4)
title('Tasa de cambio de V frente a T para p=4 at.')
xlabel('Temperatura (en K)')
ylabel('Tasa de cambio de V (en cc/K)')

Continuar

Resolución del segundo apartado

La razón de cambio del volumen respecto de la presión cuando se mantiene constante la temperatura es $\ldots$ hazlo tú y pulsa en 'Ver' cuando lo tengas.

Ver

Hemos de derivar $V=k\frac{T}{p}$ respecto de $p$: $$\frac{\partial V}{\partial p}(T,p)=-k\frac{T}{p^2}$$ Para $T=290$, la función que da el volumen en función de la presión es $$V(290,p)=k\frac{290}{p}$$ y la variación del volumen respecto de la presión es $$\frac{\partial V}{\partial p}(290,p)=-k\frac{290}{p^2}=-2379.7\frac{1}{p^2}$$ Dibujamos la gráfica del volumen frente a la presión cuando se mantiene la temperatura constantemente a 290 K y la gráfica de la variación del volumen en esas mismas circunstancias, poniendo

k=82.06;
p=3:.1:5;
V=k*290./p;
subplot(1,2,1)
plot(p,V)
title('Volumen frente a presión para T=290 K')
xlabel('Presión (en atmósferas)')
ylabel('Volumen (en cc)')
subplot(1,2,2)
plot(p,-k*290./p.^2)
title('Tasa de cambio de V frente a p para T=290 K')
xlabel('Presión (en atmósferas)')
ylabel('Tasa de cambio de V (en cc/at.)')

Continuar