Ejercicio recopilatorio sobre funciones de varias variables
Se considera la función $$f(x,y)=\sqrt{4-x^2-y^2}$$ Sabemos que es una función real de dos variables porque asigna a cada par de números reales $(x,y)$, en un cierto dominio, un único número real $f(x,y)$. Para esta función:- Encuentra el dominio y el recorrido.
- Describe su gráfica en el dominio de definición y realiza su representación.
- Escribe la expresión de sus curvas de nivel y de contorno.
- Encuentra el límite de $f(x,y)$ cuando $(x,y)$ tiende a $(1,0)$ y analiza la continuidad de la función en ese punto.
- Halla la primera derivada parcial de $f(x,y)$ respecto de $x$ en el punto $(1,0)$ utilizando la definición.
- Calcula la derivada anterior con técnicas de derivación y da dos interpretaciones de esa derivada.
- Repite los apartados anteriores para la primera derivada parcial respecto de $y$ en el mismo punto.
- Calcula las derivadas parciales segundas de $f(x,y)$ en el punto $(1,0)$.
- Halla la derivada direccional de $f(x,y)$ en $(1,0)$ en la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$ y da dos interpretaciones de ese valor.
- Aplica la derivada anterior para aproximar $f(x,y)$ en un punto próximo al $(1,0)$
- Analiza la diferenciabilidad de $f(x,y)$ en el punto $(1,0)$ y encuentra su diferencial.
- ¿Existe algún punto del dominio de $f(x,y)$ donde todas las derivadas direccionales sean nulas?
- Utiliza el gradiente de $f$ en $(1,0)$ para comprobar el cálculo de la derivada direccional del apartado 9 y para buscar las direcciones y las tasas de variación de máximo crecimiento y de máximo decrecimiento en ese punto.
- Demuestra que la curva de nivel $f(x,y)=f(1,0)$ y el gradiente de $f(x,y)$ en $(1,0)$ son ortogonales.
- Encuentra la ecuación del plano tangente a la superficie $z=f(x,y)$ en el punto $(1,0,\sqrt{3})$
- Con el plano tangente calculado, halla la aproximación lineal del valor de $f(1.1,0.2)$
- Utiliza derivadas direccionales para hacer la aproximación del apartado anterior.
- Halla la fórmula de Taylor de segundo grado centrada en $(1,0)$
1. Dominio y recorrido
El dominio de $f(x,y)$ es el conjunto de puntos del plano donde se puede definir la función, lo que significa que el radicando sea positivo, luego el dominio es ... Determínalo y pulsa en 'Ver' cuando lo tengas.
Ver
$$D_f=\{(x,y)/ \, x^2+y^2\leq 4\}$$
es decir la circunferencia de radio 2 y centro $(0,0)$ y todo su interior.
El rango o recorrido o imagen de $f(x,y)$ es el conjunto de valores reales que va tomando $f(x,y)$ cuando $(x,y)$ va recorriendo el dominio de definición. En este caso,
$f(x,y)$ es nulo o cualquier número positivo, pues se está tomando la raíz positiva
$f(x,y)$ positivo o nulo, pero nunca sobrepasa el valor 2
Es cierto que no puede ser negativo, pero observa que $4-(x^2+y^2)$ vale como mucho 4
En efecto, puesto que $4-(x^2+y^2)$ vale como mucho 4, el rango o recorrido o imagen de $f(x,y)$ son los números reales comprendidos entre 0 y 2, es decir
$$\mbox{Im}\, f=[0,2]$$
2. Gráfica de $z=f(x,y)$
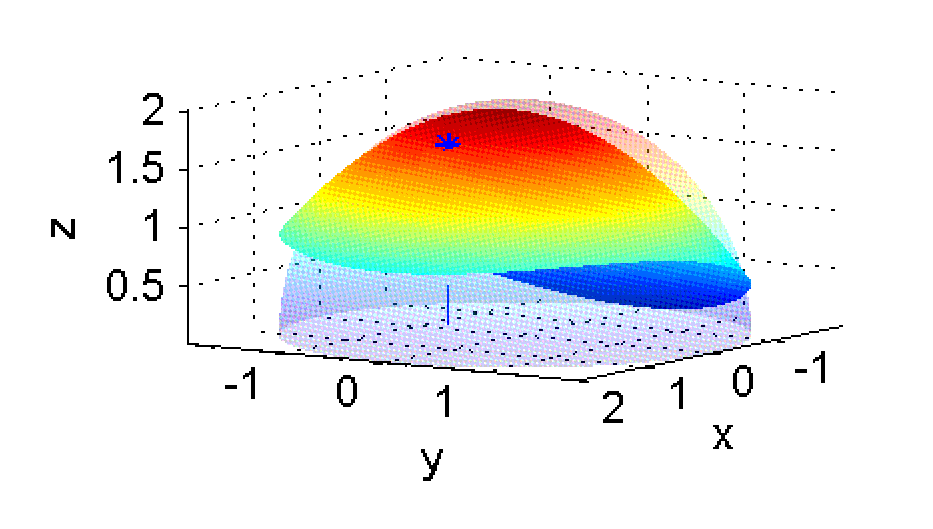
La gráfica de $z=f(x,y)$ es el conjunto de puntos de ${\bf R}^3$ de la forma $(x,y,\sqrt{4-x^2-y^2})$, que forman la superficie conocida como semiesfera superior, de centro $(0,0,0)$ y radio 2. Su representación gráfica es:
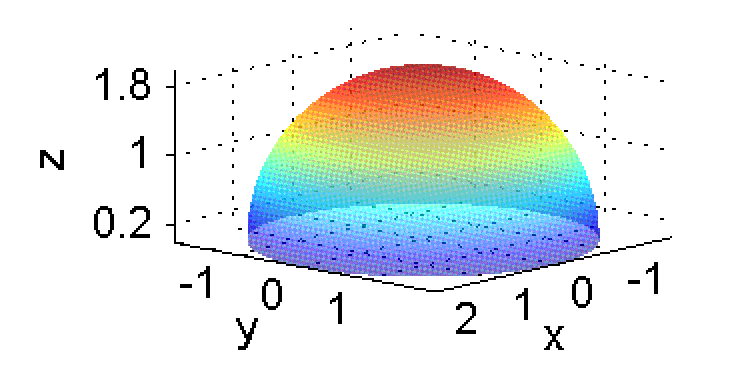
3. Curvas de nivel y de contorno
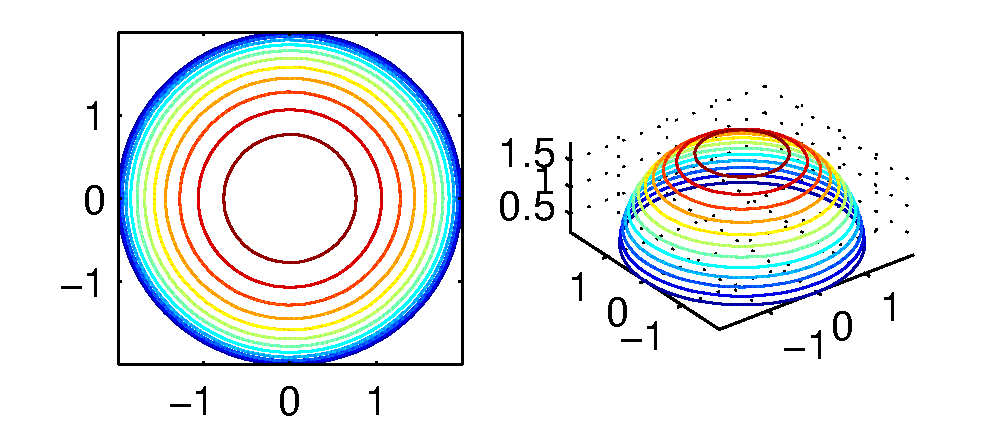
Si $k$ es un número real, pertenciente a la imagen o recorrido de $f(x,y)$, la curva de nivel de valor $k$ es el conjunto de puntos $(x,y)$ dentro del dominio de $f(x,y)$ donde $f(x,y)=k$. En este caso tendremos curva de nivel para cada $k$ entre 0 y 2, siendo la curva de nivel de valor $k$
... Encuéntrala y pulsa en 'Ver' cuando lo tengas.
Ver
la curva de nivel de valor $k$ es $$x^2+y^2=4-k^2$$
es decir, la circunferencia de centro $(0,0)$ y radio $\sqrt{4-k^2}$.
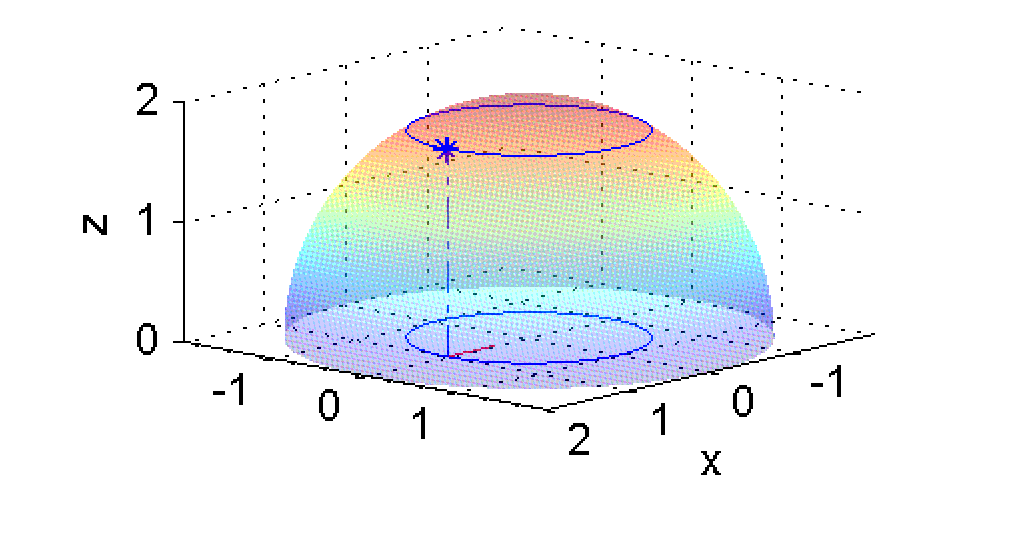
La curva de contorno de altura $k$ es esa circunferencia situada en el plano $z=k$. En la figura vemos a la izquierda una muestra de las curvas de nivel (por tanto curvas en el plano) y a la derecha las curvas de contorno correspondientes (curvas espaciales):

4. Límite y continuidad en el punto $(1,0)$
En este caso, puesto que no se produce ninguna indeterminación, sabemos por simple sustitución que
el límite de $f(x,y)$ cuando $(x,y)$ se aproxima al punto $(1,0)$ es $\sqrt{3}$, eso se escribe con la siguiente notación
$$\lim_{(x,y)\rightarrow(1,0)} f(x,y)=\sqrt{3}$$
y al coincidir el valor de ese límite con el valor de $f(1,0)$, se sabe que la función $f(x,y)$ es continua en $(x,y)=(1,0)$.
5. Derivada parcial respecto de $x$ en el punto $(1,0)$
La derivada parcial de $f(x,y)$ respecto de $x$ en el punto $(1,0)$ se define por
$$\lim_{\Delta x\rightarrow 0}\frac{f(1+\Delta x,0)-f(1,0)}{\Delta x}$$ se denota por $f'_x(1,0)$
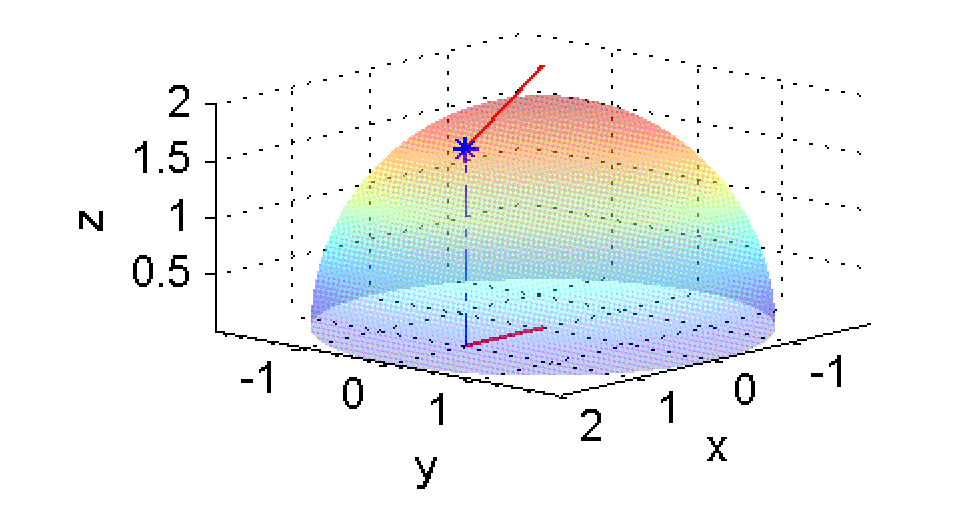
y es la pendiente de la curva intersección entre el plano $y=0$ y la superficie $z=\sqrt{4-x^2-y^2}$. En las figuras siguientes está marcada en azul esa curva intersección y en rojo un segmento de la recta tangente en el punto $(1,0,\sqrt{3})$:
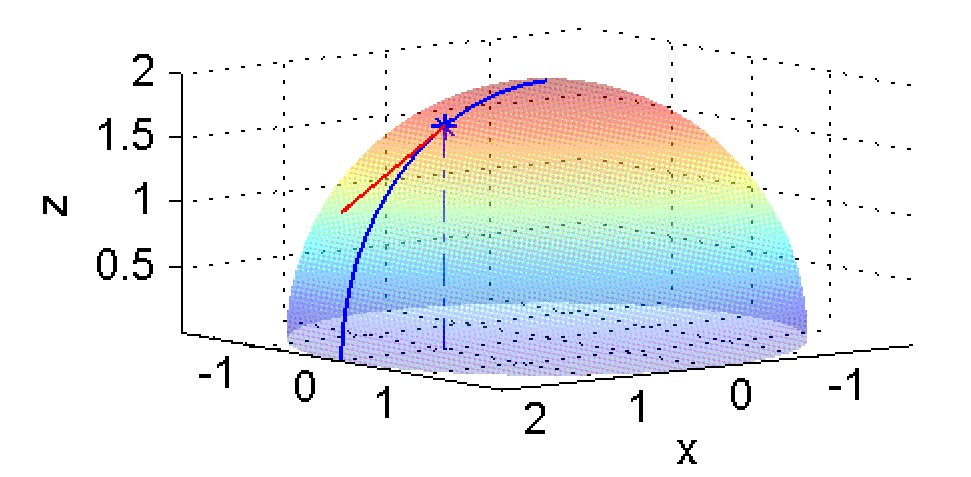
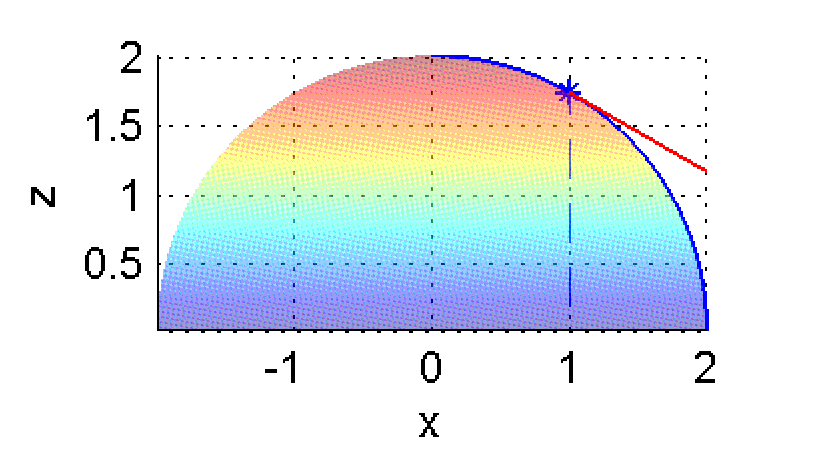
Ahora has de calcular el límite anterior, pulsa en 'Ver' cuando lo tengas.


Ahora has de calcular el límite anterior, pulsa en 'Ver' cuando lo tengas.
Ver
$$f'_x(1,0)=\lim_{\Delta x\rightarrow 0}\frac{\sqrt{4-(1+\Delta x)^2}-\sqrt{3}}{\Delta x}=
\lim_{\Delta x\rightarrow 0}\frac{\sqrt{3-2\Delta x-\Delta x ^2}-\sqrt{3}}{\Delta x}=$$ $$
=\lim_{\Delta x\rightarrow 0}\frac{3-2\Delta x-\Delta x ^2-3}{\Delta x (\sqrt{3-2\Delta x-\Delta x ^2}+\sqrt{3})}
=\lim_{\Delta x\rightarrow 0}\frac{-2-\Delta x}{\sqrt{3-2\Delta x-\Delta x ^2}+\sqrt{3}}=
\frac{-2}{2\sqrt{3}}=\frac{-1}{\sqrt{3}}=\frac{-\sqrt{3}}{3}$$
6. Cálculo de la derivada parcial con técnicas de derivación
Debemos obtener el mismo valor del apartado anterior, pero ahora derivando con las técnicas de derivación conocidas para funciones de una variable: al derivar la expresión $f(x,y)=\sqrt{4-x^2-y^2}$ respecto de $x$, dejando la $y$ constante, tendremos que
$f'_x(x,y)=\frac{-x-y}{\sqrt{4-x^2-y^2}}$
$f'_x(x,y)=\frac{1}{2\sqrt{4-x^2-y^2}}$
$f'_x(x,y)=\frac{-x}{\sqrt{4-x^2-y^2}}$
No es correcto, recuerda que la $y$ se comporta como una constante
No es correcto, no estás aplicando bien la regla de la derivación compuesta
En efecto, esa es la expresión de la derivada para cualquier $(x,y)$. Ahora sólo falta evaluarla en $(1,0)$; pulsa en 'Ver' cuando lo tengas.
$$f'_x(x,y)=\frac{-x}{\sqrt{4-x^2-y^2}} \ \ \Rightarrow \ \ f'_x(1,0)=\frac{-\sqrt{3}}{3}$$
que es en efecto el mismo valor obtenido mediante la definición. Pensamos ahora en dos interpretaciones para este valor:
- Si la función $f(x,y)$ diera la altura correspondiente a cada punto $(x,y)$ del plano (orientado éste con la dirección norte hacia arriba), la derivada $f'_x(1,0)=\frac{-\sqrt{3}}{3}$ sería la pendiente cuando se sale del punto $(1,0,\sqrt{3})$ en dirección ...
Norte
Oeste
Este
No, la variable $y$ se mantiene constantemente a 0, luego el movimiento es horizontal;
No, se está derivando en sentido creciente de la $x$;
En efecto, el movimiento es horizontal y en sentido creciente de la $x$.
- Si la función $f(x,y)$ fuera la temperatura en cada punto $(x,y)$ de una placa plana, la derivada $f'_x(1,0)$ sería la tasa de cambio o velocidad de cambio de la temperatura cuando ... (piénsalo y pulsa en 'Ver')
Ver
se sale desde el punto $(1,0)$ manteniendo la coordenada $y$ constante en sentido creciente de la coordenada $x$ (es decir, moviéndonos horizontalmente hacia la derecha).
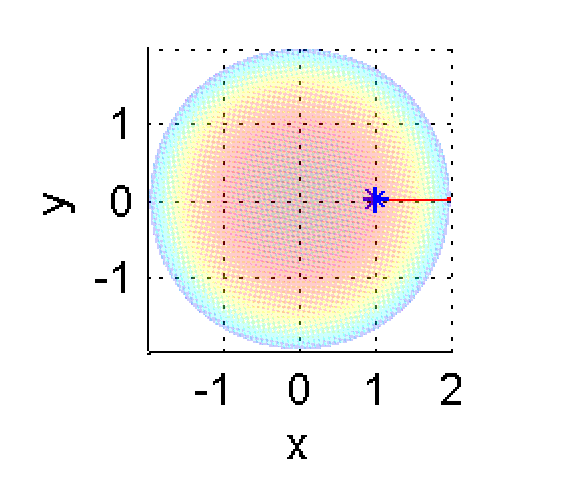

7. Primera derivada parcial respecto de $y$ en $(1,0)$
La derivada parcial de $f(x,y)$ respecto de $y$ en el punto $(1,0)$ se define por
$$\lim_{\Delta y\rightarrow 0}\frac{f(1,\Delta y)-f(1,0)}{\Delta y}$$ se denota por $f'_y(1,0)$
y es la pendiente de la curva intersección entre el plano $x=1$ y la superficie $z=\sqrt{4-x^2-y^2}$. En las figuras siguientes está marcada en azul esa curva intersección y en verde un segmento de la recta tangente en el punto $(1,0,\sqrt{3})$:
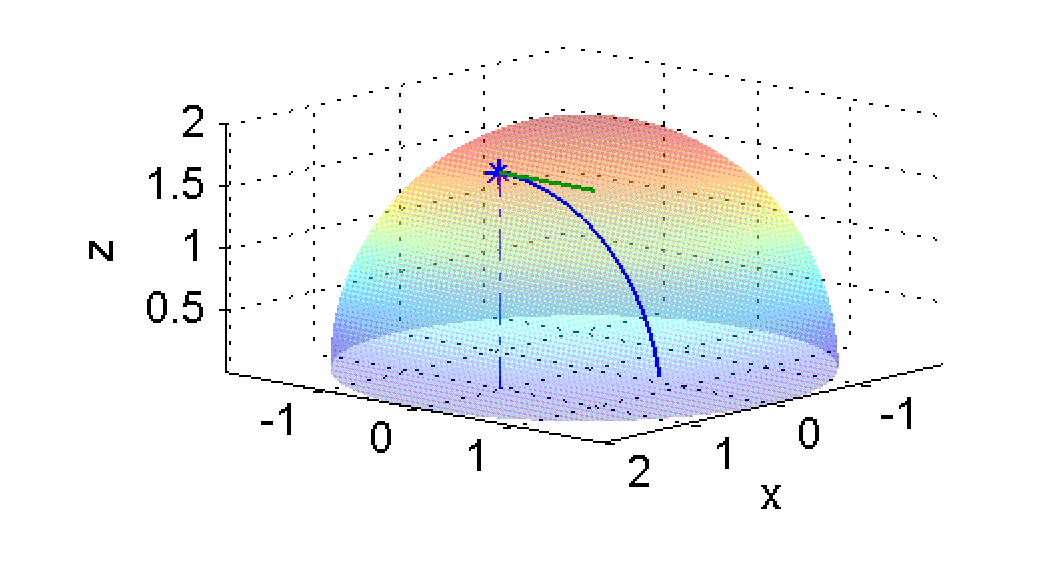
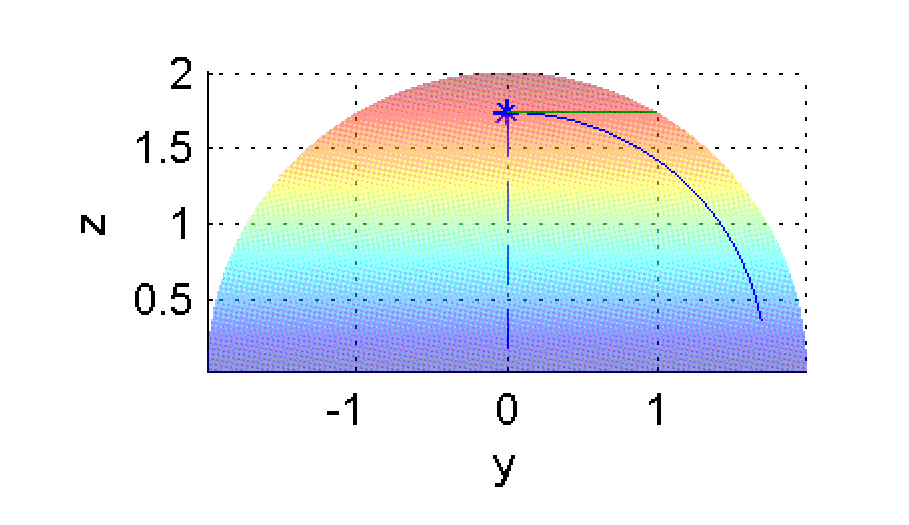
Calcula el límite anterior y pulsa en 'Ver' cuando termines.


Calcula el límite anterior y pulsa en 'Ver' cuando termines.
Ver
$$f'_y(1,0)=\lim_{\Delta y\rightarrow 0}\frac{f(1,\Delta y)-f(1,0)}{\Delta y}=\lim_{\Delta y\rightarrow 0}
\frac{\sqrt{4-1-\Delta y^2}-\sqrt{3}}{\Delta y}=$$ $$=\lim_{\Delta y\rightarrow 0}
\frac{3-\Delta y^2-3}{\Delta y(\sqrt{3-\Delta y^2}+\sqrt{3})}=\lim_{\Delta y\rightarrow 0}\frac{-\Delta y}{\sqrt{3-\Delta y^2}+\sqrt{3}}=0$$
Este es el mismo valor que habríamos obtenido derivando, con las técnicas de derivación conocidas, la expresión $f(x,y)=\sqrt{4-x^2-y^2}$ respecto de $y$, es decir, dejando la $x$ como constante, y después evaluando en $(1,0)$ la expresión obtenida:
$$f'_y(x,y)=\frac{-y}{\sqrt{4-x^2-y^2}} \ \ \Rightarrow \ \ f'_y(1,0)=0$$
Por ejemplo
- si la función $f(x,y)$ fuera la altura de una montaña, la derivada $f'_y(1,0)$ sería la pendiente cuando se sale del punto $(1,0,\sqrt{3})$ en dirección Norte;
- si la función $f(x,y)$ fuera la temperatura en cada punto $(x,y)$ de la placa de la figura, la derivada $f'_y(1,0)$ sería la tasa de cambio o velocidad de cambio de la temperatura cuando se sale desde el punto $(1,0)$ manteniendo la coordenada $x$ constante en sentido creciente de la coordenada $y$ (es decir, moviéndonos verticalmente hacia arriba).
8. Derivadas parciales segundas en el punto $(1,0)$
En primer lugar calculamos las derivadas para cualquier punto $(x,y)$. Para hallar la derivada respecto de $x$ dos veces, derivamos la función $f'_x(x,y)$ respecto de $x$. Hazlo y pulsa en 'Ver' cuando lo tengas.
Ver
$$f'_x(x,y)=\frac{-x}{\sqrt{4-x^2-y^2}} \ \ \Rightarrow \ \ f''_{xx}(x,y)=\frac{y^2-4}{(4-x^2-y^2)^{3/2}}$$
Si procedemos de esta forma para $f''_{xy}$, $f''_{yx}$ y $f''_{yy}$, determinaremos que ... (deriva y pulsa en 'Ver')
$$f''_{xx}(x,y)=\frac{y^2-4}{(4-x^2-y^2)^{3/2}}\ \ , \ \ f''_{xy}(x,y)=\frac{-xy}{(4-x^2-y^2)^{3/2}}=f''_{yx}(x,y)\ \ , \ \ f''_{yy}(x,y)=\frac{x^2-4}{(4-x^2-y^2)^{3/2}}$$
Ahora hay que evaluarlas en el punto $(1,0)$, hazlo y pulsa en 'Ver'.
Ver
En el punto $(1,0)$, las derivadas segundas valen
$$f''_{xx}(1,0)=\frac{-4}{9}\sqrt{3}\ \ , \ \ f''_{xy}(1,0)=0=f''_{yx}(1,0)\ \ , \ \ f''_{yy}(1,0)=\frac{-\sqrt{3}}{3}$$
9. Derivada direccional de $f(x,y)$ en $(1,0)$ en la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$
La derivada direccional de $f(x,y)$ en $(1,0)$ en la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$ es
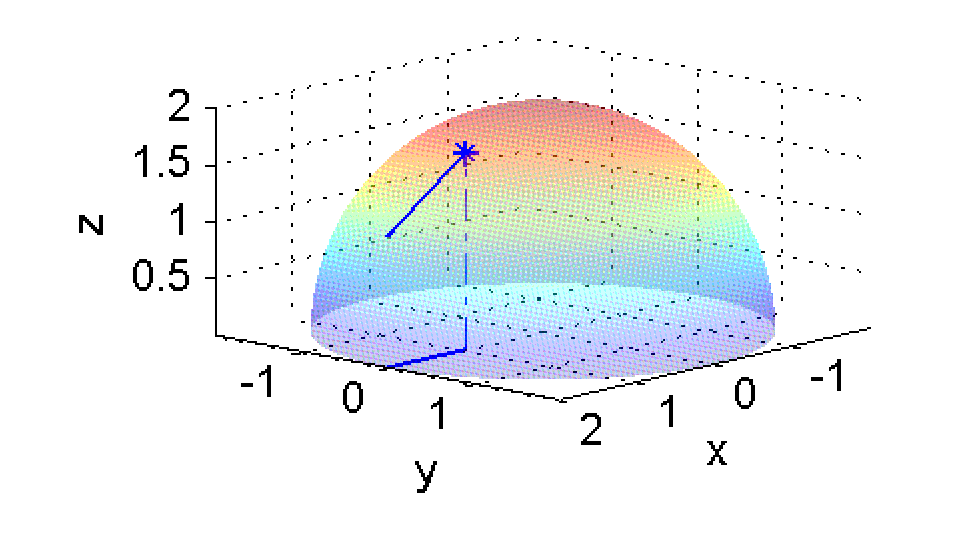
$$D_{\bf u}f(1,0)=\lim_{h\rightarrow 0}\frac{f(1+\sqrt{2} h/2,\sqrt{2} h/2)-f(1,0)}{h}$$ y es el valor de la pendiente de la curva intersección entre la superficie $z=f(x,y)$ y el plano vertical que contiene al vector ${\bf u}$. En la figura de la izquierda se ha dibujado la dirección ${\bf u}$ en el plano, situada sobre el punto $(1,0)$; a la derecha vemos el vector tangente a la curva intersección entre la superficie y el plano que contiene a ${\bf u}$; las componentes de ese vector tangente (espacial) son $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},D_{\bf u}f(1,0))$:
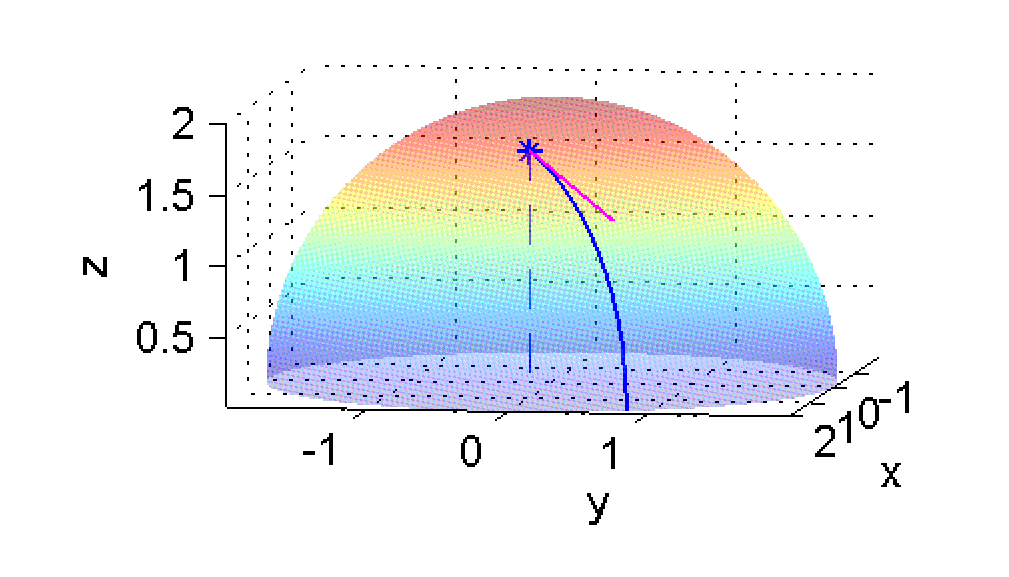
Calcula el límite anterior y pulsa en 'Ver' cuando lo tengas.


Calcula el límite anterior y pulsa en 'Ver' cuando lo tengas.
Ver
$$D_{\bf u}f(1,0)=\lim_{h\rightarrow 0}\frac{f(1+\sqrt{2} h/2,\sqrt{2} h/2)-f(1,0)}{h}=\lim_{h\rightarrow 0}
\frac{\sqrt{4-(1+\sqrt{2} h/2)^2-(\sqrt{2} h/2)^2}-\sqrt{3}}{h}=$$
$$=\lim_{h\rightarrow 0}
\frac{\sqrt{4-1-\sqrt{2} h-h^2/2-h^2/2}-\sqrt{3}}{h}=\lim_{h\rightarrow 0}
\frac{\sqrt{3-\sqrt{2} h-h^2}-\sqrt{3}}{h}=$$
$$=\lim_{h\rightarrow 0}\frac{3-\sqrt{2} h-h^2-3}{h(\sqrt{3-\sqrt{2} h-h^2}+\sqrt{3})}=
\lim_{h\rightarrow 0}\frac{-\sqrt{2} -h}{\sqrt{3-\sqrt{2} h-h^2}+\sqrt{3}}=\frac{-\sqrt{2}}{2\sqrt{3}}=\frac{-\sqrt{6}}{6}$$
Utilizando los dos significados dados antes para la función $f(x,y)$,
- si la función $f(x,y)$ fuera la altura de una montaña, la derivada $D_{\bf u}f(1,0)$ sería la pendiente en el punto $(1,0,\sqrt{3})$ cuando se sale de él en dirección Noreste;
- si la función $f(x,y)$ fuera la temperatura en cada punto $(x,y)$ de la placa de la figura, la derivada $D_{\bf u}f(1,0)$ sería la tasa de cambio o velocidad de cambio de la temperatura cuando se sale desde el punto $(1,0)$ hacia cualquier otro punto de la semirrecta $y=x-1$ con $x>1$, por ejemplo el punto $(1.2, 0.2)$
10. Aproximación de $f(x,y)$ en un punto próximo al $(1,0)$ sobre la semirrecta $y=x-1$, $x>1$
Esa derivada direccional puede utilizarse para aproximar el valor de la función en un punto cercano al $(1,0)$ que esté en la semirrecta $y=x-1$ con $x>1$. Por ejemplo la variación de $f(x,y)$ entre los puntos $(1,0)$ y $(1.2, 0.2)$ se puede aproximar por el producto del módulo del vector $(0.2,0.2)$ por la derivada direccional calculada antes:
$$f(1.2,0.2)-f(1,0)\approx (0.2,0.2)\frac{-\sqrt{6}}{6}=(1,1)\frac{-\sqrt{6}}{30}$$
$$f(1.2,0.2)-f(1,0)\approx |(0.2,0.2)|\frac{-\sqrt{6}}{6}=\frac{-\sqrt{3}}{15}$$
No, ¡Un escalar no puede ser igual a un vector! has olvidado tomar el módulo de $(0.2,0.2)$
En efecto, esa sería una aproximación del cambio que sufre $f(x,y)$ cuando se va desde $(1,0)$ hasta $(1.2,0.2)$. En vez de ir desde $(1,0,\sqrt{3})$ a $(1.2,0.2,f(1.2,0.2))$ por la superficie, vamos por la recta tangente en $(1,0,\sqrt{3})$ a la curva que pasa por $(1,0,\sqrt{3})$ y que está contenida a la vez en la superficie y en el plano vertical que contiene al vector ${\bf u}$; el incremento que sufre la tercera componente de esa recta tangente al pasar de $(1,0)$ a $(1.2,0.2)$ es $\frac{-\sqrt{3}}{15}$:


11. Diferenciabilidad y diferencial de $f(x,y)$ en el punto $(1,0)$
Analizamos ahora la diferenciabilidad de la función $f(x,y)=\sqrt{4-x^2-y^2}$. Recurrimos para ello al teorema que da las condiciones suficientes de diferenciabilidad:
- la función $f(x,y)$ es continua en su dominio de definición
- las derivadas parciales (sólo haría falta una) son continuas en todos los puntos del dominio en los que $x^2+y^2\neq 4$
$(f'_x(1,0),f'_y(1,0))=(\frac{-\sqrt{3}}{3},0)$
$(f'_x(1,0)\, dx,f'_y(1,0)\, dy)=(\frac{-\sqrt{3}}{3}\, dx,0)$
$(f'_x(1,0),f'_y(1,0))\cdot(dx,dy)=f'_x(1,0)\, dx+f'_y(1,0)\, dy=\frac{-\sqrt{3}}{3}\, dx$
No, eso es el gradiente de $f(x,y)$ en el punto $(1,0)$;
No, no buscamos un vector
En efecto, $df(1,0)=\frac{-\sqrt{3}}{3}\, dx$.
12. ¿Derivadas direccionales todas nulas?
Si en un punto $(x,y)$ la función es diferenciable, entonces la derivada direccional es el producto escalar de la dirección por el gradiente en ese punto. Por tanto
las derivadas direccionales son todas nulas si el gradiente en ese punto lo es. Puesto que
$$f'_x(x,y)=\frac{-x}{\sqrt{4-x^2-y^2}} \ \ ,\ \ f'_y(x,y)=\frac{-y}{\sqrt{4-x^2-y^2}}$$
las derivadas direccionales son todas nulas si el punto $(x,y)$ es ... Piénsalo y pulsa en 'Ver'.
Ver
El único punto donde se anulan simultáneamente las dos derivadas parciales primeras es el $(0,0)$. En consecuencia, todas las derivadas direccionales de $f(x,y)$ en $(0,0)$ son nulas y el plano tangente a la gráfica de $z=f(x,y)$ en el punto $(0,0,2)$ es el plano de ecuación $z=2$.
13. Cálculo de la derivada direccional y búsqueda de las direcciones y las tasas de variación de máximo crecimiento y de máximo decrecimiento.
Puesto que $f(x,y)$ es diferenciable en $(1,0)$, su gradiente en $(1,0)$, que es
$$\nabla f(1,0)=\left(\frac{-\sqrt{3}}{3},0\right)$$
nos sirve para hallar cualquier otra derivada direccional en ese punto $(1,0)$. Por ejemplo, la derivada direccional en $(1,0)$ en la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$ se puede calcular haciendo el siguiente producto escalar:
$$D_{\bf u}f(1,0)=\nabla f(1,0)\cdot {\bf u}=\frac{\sqrt{2}}{2}\left(\frac{-\sqrt{3}}{3},0\right)\cdot(1,1)=\frac{\sqrt{2}}{2}\frac{-\sqrt{3}}{3}=
\frac{-\sqrt{6}}{6}$$
que es el valor obtenido antes aplicando la definición de derivada direccional y calculando el límite. Además, la dirección en la que el producto escalar sea máximo será la propia del gradiente, así que la dirección de mayor crecimiento saliendo desde el punto $(1,0)$ es
$\nabla f(1,0)=\left(\frac{-\sqrt{3}}{3},0\right)$
$|\nabla f(1,0)|=\frac{\sqrt{3}}{3}$
$\frac{\nabla f(1,0)}{|\nabla f(1,0)|}=\sqrt{3}\left(\frac{-\sqrt{3}}{3},0\right)=(-1,0)$
No, eso no es una dirección. Una dirección tiene módulo 1.
No, eso es la tasa de variación, no la dirección.
Correcto, esa es la dirección de máximo crecimiento de la función desde el punto $(1,0)$ y la tasa de variación en ese punto en esa dirección (por tanto tasa de variación máxima en ese punto) es $|\nabla f(1,0)|=\frac{\sqrt{3}}{3}$
Puesto que en el punto $(1,0)$ la dirección de máximo crecimiento es $(-1,0)$, la dirección de máximo decrecimiento desde ese punto es la opuesta, es decir
$$\frac{-\nabla f(1,0)}{|\nabla f(1,0)|}=\sqrt{3}\left(\frac{\sqrt{3}}{3},0\right)=(1,0)$$ y el valor de la mínima derivada direccional (en ese punto) es $$-|\nabla f(1,0)|=-\frac{\sqrt{3}}{3}$$
A la izquierda, en el plano $XY$ se ha representado el vector $(-1,0)$, que es aquí la dirección de máximo crecimiento de la función, y también vemos el vector $(-1,0,\frac{\sqrt{3}}{3})$ en la superficie; a la derecha vemos en el plano $XY$ la dirección de máximo decrecimiento, $(1,0)$, y el vector $(1,0,-\frac{\sqrt{3}}{3})$ en la superficie:
En los casos mencionados antes,


En los casos mencionados antes,
- si la función $f(x,y)$ fuera la altura de una montaña, desde el punto $(1,0,\sqrt{3})$ saldríamos en dirección Oeste si queremos la mayor pendiente positiva y en dirección Este si queremos bajar lo más rápidamente posible; si en el punto $(1,0,\sqrt{3})$ soltáramos una bola, la dirección de caída sería ésta última y el vector tangente a la trayectoria de la bola sería $(1,0,-\frac{\sqrt{3}}{3})$;
- si la función $f(x,y)$ fuera la temperatura en cada punto $(x,y)$ de la placa plana, de todas las direcciones posibles desde el punto $(1,0)$ tendremos que elegir ir horizontalmente hacia la izquierda si queremos el aumento mayor de temperatura y nos moveremos horizontalmente hacia la derecha para conseguir la mayor disminución de temperatura.
14. Ortogonalidad entre la curva de nivel $f(x,y)=f(1,0)$ y el gradiente de $f(x,y)$ en $(1,0)$
En primer lugar debemos encontrar la curva de nivel de $z=f(x,y)$ que pasa por el punto $(1,0)$, que es el lugar geométrico de los puntos que cumplen que $f(x,y)=f(1,0)$. Hazlo y pulsa en 'Ver'.
Ver
$$f(x,y)=f(1,0) \ \ \Leftrightarrow\ \ \sqrt{4-x^2-y^2}=\sqrt{3}\ \ \Rightarrow \ \ x^2+y^2=1$$
Para comprobar que esta curva es ortogonal en el punto $(1,0)$ al vector gradiente, encontramos el vector tangente a la curva en el punto $(1,0)$:
Despejando $y=\sqrt{1-x^2}$ y derivando después respecto de $x$: $y'(x)=\frac{dy}{dx}$; el vector tangente es $(1,y'(1))$
Ninguna de las dos opciones presentadas es correcta
Despejando $x=\sqrt{1-y^2}$ y derivando después respecto de $y$: $x'(y)=\frac{dx}{dy}$; el vector tangente es $(x'(0),1)$
No, en este caso no se puede hacer así, pues la función $y=\sqrt{1-x^2}$ no es derivable respecto de $x$ en $x=1$. De hecho, la ecuación $x^2+y^2=1$ no define a $y$ como función de $x$ en un entorno del punto $(1,0)$.
No, sí que hay una opción correcta.
Correcto, la ecuación $x^2+y^2=1$ no define a $y$ como función de $x$ en un entorno del punto $(1,0)$ pero sí define a $x$ como función de $y$, luego podemos encontrar el vector tangente a la curva haciendo $$(x'(0),1)=(0,1)$$
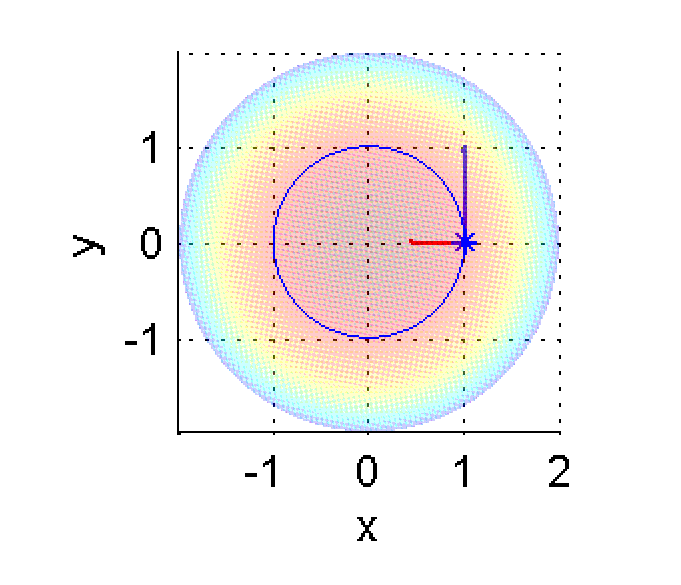
El vector tangente a la curva de nivel en el punto $(1,0)$ es el vector $(0,1)$ y el vector gradiente es $\nabla f(1,0)=\left(\frac{-\sqrt{3}}{3},0\right)$, luego es evidente que son ortogonales. En la figura siguiente se representa a la izquierda la curva de contorno, la curva de nivel y el vector gradiente; a la derecha vemos la curva de nivel, en rojo el vector gradiente de $f$ en $(1,0)$ y en azul el vector tangente a la curva:


15. Ecuación del plano tangente a la superficie $z=f(x,y)$ en el punto $(1,0,\sqrt{3})$
Calcularemos ahora la ecuación del plano tangente a $z=f(x,y)$ en $(1,0,\sqrt{3})$. Conocemos dos vectores que pertenecen a ese plano, pues cada uno de ellos es tangente a una curva contenida en la superficie:
- el vector ${\bf T}'_{\bf u}=(1,0,f'_x(1,0))=(1,0,\frac{-\sqrt{3}}{3})$ que es tangente a la curva intersección de $z=f(x,y)$ con el plano $y=0$
- el vector ${\bf T}'_{\bf v}=(0,1,f'_y(1,0))=(0,1,0)$ que es tangente a la curva intersección de $z=f(x,y)$ con el plano $x=1$
Ver
$${\bf N}=\left|\begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\
1 & 0 & \frac{-\sqrt{3}}{3} \\
0& 1 & 0
\end{array}\right|=\left(\frac{\sqrt{3}}{3},0,1\right)$$ En la figura vemos los dos vectores tangentes ${\bf T}'_{\bf u}$ y ${\bf T}'_{\bf v}$ así como el vector normal ${\bf N}$:
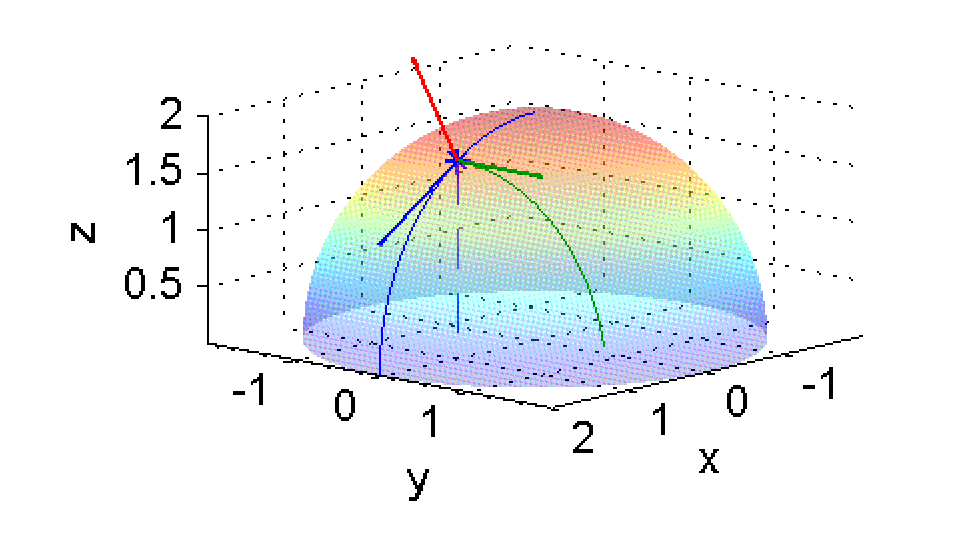

A partir de aquí, la ecuación del plano se obtiene de hacer ${\bf N}\cdot (x-1,y,z-\sqrt{3})=0$, es decir $$\frac{\sqrt{3}}{3}(x-1)+0(y-0)+(z-\sqrt{3})=0$$ que es lo mismo que
$$z=\frac{\sqrt{3}}{3}(4-x)$$
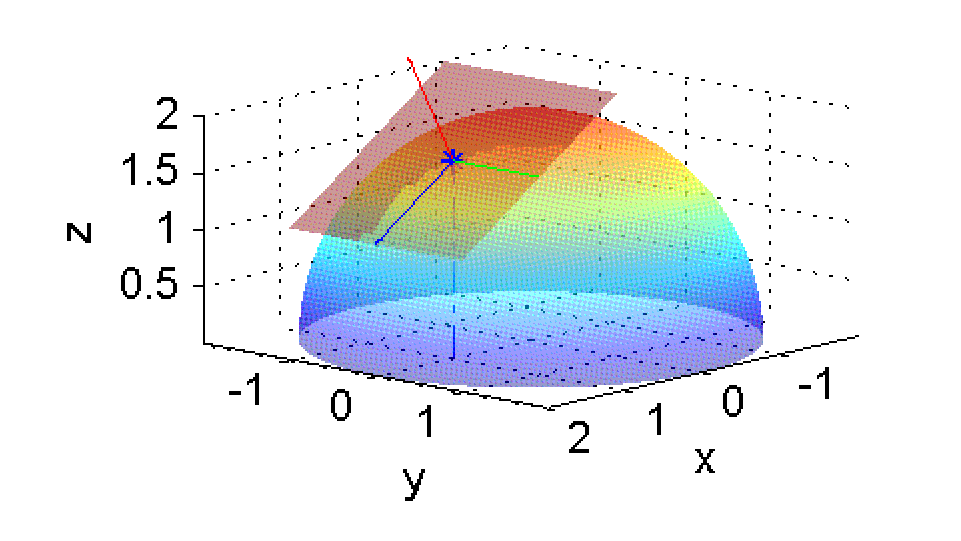
Este plano coincide con la superficie $z=f(x,y)$ en que ambas pasan por el punto $(1,0,\sqrt{3})$ y en el valor de las primeras derivadas parciales en $(1,0)$. En consecuencia, este plano tangente contiene a todos los vectores de la forma $(v_1,v_2,D_{\bf v}(1,0))$ siendo ${\bf v}=(v_1,v_2)$ una dirección cualquiera. Por ejemplo el vector formado con la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$ y la derivada direccional de $f(x,y)$ en la dirección ${\bf u}$ que se ha calculado antes: $$\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},\frac{-\sqrt{6}}{6}\right)$$

Este plano coincide con la superficie $z=f(x,y)$ en que ambas pasan por el punto $(1,0,\sqrt{3})$ y en el valor de las primeras derivadas parciales en $(1,0)$. En consecuencia, este plano tangente contiene a todos los vectores de la forma $(v_1,v_2,D_{\bf v}(1,0))$ siendo ${\bf v}=(v_1,v_2)$ una dirección cualquiera. Por ejemplo el vector formado con la dirección ${\bf u}=\frac{\sqrt{2}}{2}(1,1)$ y la derivada direccional de $f(x,y)$ en la dirección ${\bf u}$ que se ha calculado antes: $$\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},\frac{-\sqrt{6}}{6}\right)$$
16. Aproximación lineal del valor de $f(1.1,0.2)$
En un entorno del punto $(1,0)$ podemos utilizar el plano tangente para hacer aproximación lineal del valor que toma $f(x,y)$ en un punto cercano $(x,y)=(1+\Delta x, \Delta y)$:
$$f(1+\Delta x, \Delta y)\approx f(1,0) +f'_x(1,0)\Delta x+ f'_y(1,0)\Delta y= \sqrt{3}-\frac{\sqrt{3}}{3} \Delta x$$
El valor aproximado de $f(1.1,0.2)$ será por tanto... calcúlalo y pulsa en 'Ver'.
Ver
En este caso $\Delta x=0.1$ e $\Delta y=0.2$, luego $$f(1.1, 0.2)\approx f(1,0) +0.1 f'_x(1,0) + 0.2 f'_y(1,0)= \sqrt{3}-\frac{\sqrt{3}}{30}$$
Por ejemplo, si la función $f(x,y)$ fuera la temperatura de una placa y se quisiera aproximar el cambio de temperatura cuando desde $(1,0)$ se avanza hasta $(1.1,0.2)$, se calcularía
$$\Delta f= f(1.1,0.2)-f(1,0) \approx \frac{-\sqrt{3}}{3} 0.1 =\frac{-\sqrt{3}}{30}$$ Este incremento se daría en las mismas unidades que la temperatura.
17. Aproximación del incremento de $f$ mediante derivadas direccionales
Es importante no equivocar el cálculo de $\Delta f$ realizado en el apartado anterior con el de la derivada direccional de $f(x,y)$ en la dirección del vector que une el punto $(1,0)$ con el punto $(1.1,0.2)$; esta derivada direccional es la tasa de cambio de $f(x,y)$ cuando se sale desde $(1,0)$ hacia $(1.1,0.2)$ y no debe equivocarse con el cambio o incremento de la función. Calculamos ahora la derivada direccional en $(1,0)$ cuando se sale hacia $(1.1,0.2)$:
$D_{\bf s}f(1,0)=\nabla f(1,0) \cdot {\bf s}=\left(\frac{-\sqrt{3}}{3},0\right)\cdot (0.1,0.2)=\frac{-\sqrt{3}}{30}$
Ninguna de las dos opciones presentadas es correcta
$D_{\bf s}f(1,0)=\nabla f(1,0) \cdot {\bf s}=\frac{\sqrt{5}}{5}\left(\frac{-\sqrt{3}}{3},0\right)\cdot (1,2)=\frac{-\sqrt{15}}{15}$
No, has olvidado dividir por su módulo el vector que une $(1,0)$ con $(1.1,0.2)$, para que ${\bf s}$ sea una dirección.
No, sí que hay una opción correcta.
Correcto, en primer lugar has calculado la dirección ${\bf s}$, restando las componentes del los puntos final e inicial y dividiendo por el módulo del vector resultante:
$$(1.1,0.2)-(1,0)=(0.1,0.2)\ \ \Rightarrow \ \ {\bf s}=\frac{10}{\sqrt{5}}\left(\frac{1}{10},\frac{2}{10}\right)=\frac{\sqrt{5}}{5}(1,2)$$
y después has multiplicado escalarmente el gradiente por la dirección.
Por tanto $\frac{-\sqrt{15}}{15}$ es la tasa de cambio de la función en el punto $P=(1,0)$ cuando se sale de este punto hacia el $Q=(1.1,0.2)$. En el ejemplo de la temperatura, esta tasa de cambio se medirá en la unidad de temperatura dividida entre la unidad de longitud en que se esté midiendo $x$ e $y$. Si multiplicamos el valor de esta derivada direccional por el módulo del vector ${\bf PQ}=(0.1,0.2)$ obtendremos la estimación para el incremento que resultó antes utilizando la diferencial $$\Delta f=f(Q)-f(P) \approx D_{\bf s}f(P) |{\bf PQ}|=\frac{-\sqrt{15}}{15}\frac{\sqrt{5}}{10}=\frac{-\sqrt{3}}{30}$$
18. Fórmula de Taylor de segundo grado centrada en $(1,0)$
La fórmula de Taylor de $f(x,y)$ centrada en $(1,0)$ es
$$f(x,y)=f(1,0)+f'_x(1,0)(x-1)+f'_y(1,0)y+\frac{1}{2}[f''_{xx}(1,0)(x-1)^2+2f''_{xy}(1,0)(x-1)y+f''_{yy}(1,0)y^2]+R_2$$
siendo $R_2$ un infinitésimo para $(x,y)$ tendiendo a $(1,0)$. Las derivadas de primer y segundo orden ya están calculadas en apartados anteriores,
$$f'_x(1,0)=\frac{-\sqrt{3}}{3}\ \ , \ \ f'_y(1,0)=0 \ \ , \ \ f''_{xx}(1,0)=\frac{-4}{9}\sqrt{3}\ \ , \ \ f''_{xy}(1,0)=0\ \ , \ \ f''_{yy}(1,0)=\frac{-\sqrt{3}}{3}$$
así que la fórmula de Taylor será ... escríbela y pulsa en 'Ver' cuando la tengas.
Ver
$$f(x,y)=\sqrt{3}-\frac{\sqrt{3}}{3}(x-1)+\frac{1}{2}\left[\frac{-4}{9}\sqrt{3}(x-1)^2-\frac{\sqrt{3}}{3}y^2\right]+R_2$$
o bien $$f(x,y)=\sqrt{3}-\frac{\sqrt{3}}{3}(x-1)-\frac{\sqrt{3}}{18}\left[4(x-1)^2+3y^2\right]+R_2$$
La parte polinómica de esta expresión es el polinomio de Taylor de segundo grado de la función $f(x,y)$ centrado en $(1,0)$:
$$T_2(x,y)=\sqrt{3}-\frac{\sqrt{3}}{3}(x-1)-\frac{\sqrt{3}}{18}\left[4(x-1)^2+3y^2\right]$$
Este polinomio coincide con $f(x,y)$ en los valores que toman en el punto $(1,0)$ así como en las primeras y segundas derivadas parciales en ese punto. En la figura siguiente se ha representado sobre la superficie $z=f(x,y)$ (más transparente) el polinomio $T_2(x,y)$, en el mismo dominio: