Enunciado
- Dibuja la gráfica de $z=x-2t+(x+2t)^3$ y en otra figura las de $z''_{tt}$ y $z''_{xx}$ juntas.
- Idem para $z=\cos (x-3t)+\mbox{sen}\, (x+3t)$.
- Demuestra que $z=f(x-at)+g(x+at)$, con $f$ y $g$ funciones suficientemente derivables, $a\in{\bf R}$ cualquiera, satisface la ecuación $$z''_{tt}=a^2z''_{xx}$$
Resolución del primer apartado
Paso 1
Antes de hacer las gráficas, calculamos las derivadas; respecto de $t$: $$z=x-2t+(x+2t)^3 \hspace{.4cm} \Rightarrow \hspace{.4cm} z'_t=-2+6(x+2t)^2\hspace{.4cm} \Rightarrow \hspace{.4cm} z''_{tt}=24(x+2t)$$ y respecto de $x$: $$z=x-2t+(x+2t)^3 \hspace{.4cm} \Rightarrow \hspace{.4cm} z'_x=1+3(x+2t)^2\hspace{.4cm} \Rightarrow \hspace{.4cm} z''_{xx}=6(x+2t)$$Paso 2
Hacemos las gráficas, escribiendo[X,Y]=meshgrid(-2:.2:2); figure(1) surf(X,Y,X-2*Y+(X+2*Y).^3) shading interp figure(2) Z=X+2*Y; surf(X,Y,24*Z) shading interp hold on surf(X,Y,6*Z) hold off alpha(.8)La figura 1 nos muestra una porción de la superficie $z=x-2t+(x+2t)^3$:
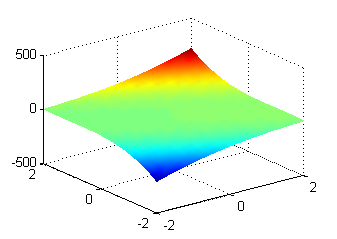
La figura 2 contiene porciones de las superficies $z''_{tt}$ (sin enrejado) y de $z''_{xx}$:
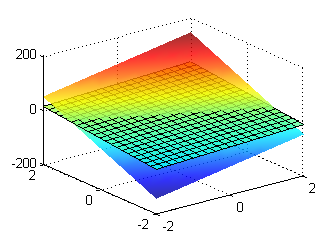
Resolución del segundo apartado
Paso 1
Igual que en el primer apartado, empezamos calculando las derivadas respecto de $t$. Hazlas tú y pulsa en 'Ver' cuando las tengas:
Ver
$$z=\cos (x-3t)+\mbox{sen}\, (x+3t) \hspace{.4cm} \Rightarrow \hspace{.4cm} z'_t=3\mbox{sen}\, (x-3t)+3\cos(x+3t)
\hspace{.4cm} \Rightarrow $$ $$\Rightarrow \hspace{.4cm} z''_{tt}=-9\cos(x-3t)-9\mbox{sen}\,(x+3t)$$
Ahora halla las derivadas respecto de $x$ y pulsa en 'Ver' cuando las tengas.
Ver
$$z=\cos (x-3t)+\mbox{sen}\, (x+3t) \hspace{.4cm} \Rightarrow \hspace{.4cm} z'_x=-\mbox{sen}\, (x-3t)+\cos(x+3t)
\hspace{.4cm} \Rightarrow $$ $$\Rightarrow \hspace{.4cm} z''_{xx}=-\cos(x-3t)-\mbox{sen}\,(x+3t)$$
Paso 2
Hacer las gráficas: escribe el código para hacer las que corresponden a este apartado y pulsa en 'Ver'.
Ver
[X,Y]=meshgrid(-2:.2:2); Z=cos(X-3*Y)+sin(X+3*Y); figure(1) surf(X,Y,Z) shading interp figure(2) surf(X,Y,-9*Z) shading interp hold on surf(X,Y,-Z) hold off alpha(.8)La figura 1 nos muestra una porción de la superficie $z=\cos (x-3t)+\mbox{sen}\, (x+3t)$:
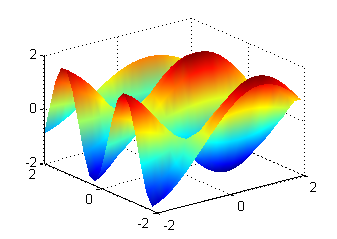
La figura 2 contiene porciones de las superficies $z''_{tt}$ (sin enrejado) y de $z''_{xx}$:
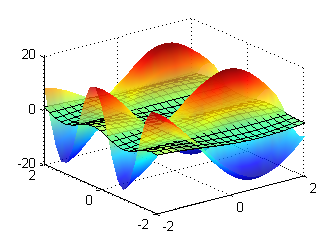
Resolución del tercer apartado
Para demostrar que $z=f(x-at)+g(x+at)$, con $f$ y $g$ funciones suficientemente derivables, $a\in{\bf R}$ cualquiera, satisface la ecuación $z''_{tt}=a^2z''_{xx}$, simplemente haremos esas derivadas y comprobaremos que cumplen la igualdad. Empezamos derivando $z$ respecto de $t$, los resultados son
$$z'_t=-af'_t(x-at)+ag'_t(x+at) \hspace{.4cm} \mbox{y} \hspace{.4cm} z''_{tt}=a^2f''_{tt}(x-at)+a^2g''_{tt}(x+at)$$
Ninguna de las opciones presentadas es correcta.
$$z'_t=-af'(x-at)+ag'(x+at) \hspace{.4cm} \mbox{y} \hspace{.4cm} z''_{tt}=a^2f''(x-at)+a^2g''(x+at)$$
Las funciones $f$ y $g$ son de una única variable, y por tanto no se derivan respecto de $t$ o respecto de $x$. Por ejemplo en el primer apartado de este ejercicio, estas funciones son $f(u)=u$ y $g(u)=u^3$ y en el segundo apartado son $f(u)=\cos u$ y $g(u)=\mbox{sen}\, u$
Hay una correcta.
En efecto, esas son las derivadas respecto de $t$. Ahora halla las derivadas respecto de $x$; pulsa después en 'Continuar'.
Las derivadas respecto de $x$ resultan
$$z'_x=f'(x-at)+g'(x+at) \hspace{.4cm} \mbox{y} \hspace{.4cm} z''_{xx}=f''(x-at)+g''(x+at)$$
Es obvio que $$z''_{tt}=a^2z''_{xx}$$
Observa que en el primer apartado, la constante es $a=2$ y la relación que se cumple es $z''_{tt}=4z''_{xx}$, mientras que en el segundo apartado se tiene $a=3$, por lo cual $z''_{tt}=9z''_{xx}$.