Ejercicios preliminares e instantáneos. Funciones de varias variables
Ejercicio 1
¿Cuáles de las siguientes expresiones son funciones de $x$ e $y$? ¿Cuáles son la ecuación de una superficie?
- $x^2+y^2=9$
- $x+y-3$
- $z=x^2+y^2$
- $z=\frac{x}{y}$
- $x^2+y^2+z^2=9$
- $z=\sqrt{3-x^2-y}$
Pista
Solución
Una función de dos variables asigna a cada $(x,y)$ un número real único, así que se expresa con la ecuación $z=f(x,y)$. Una superficie puede ser la gráfica de una función de dos variables en un cierto dominio, pero también es el conjunto de puntos que satisfacen una expresión implícita, del tipo $F(x,y,z)=0$.
Son funciones de $x$ e $y$ las expresiones de los apartados c), d) y f).
Son ecuaciones de superficies todas menos la expresión del apartado b), que no es una ecuación.
Ejercicio 2
Para cada una de las familias de curvas siguientes, representa en una figura las curvas correspondientes a cinco valores diferentes de $k$.
- $x+y=k$
- $x^2+y^2=k$
- $y=kx$
- $x^2+k=y$
Solución
- $x+y=k$: es una familia de rectas, que se caracterizan por tener pendiente 1; podemos tomar por ejemplo $$x+y=-2\ ,\ \ x+y=-1\ ,\ \ x+y=0\ ,\ \ x+y=1\ ,\ \ x+y=2$$
Para dibujarlas en el ordenador generamos una matriz; en cada columna se guardan los valores de la recta correspondiente a un valor de $k$:
x=-3:.1:3; k=-2:2; for n=1:5 y(:,n)=k(n)-x; end plot(x,y) title('muestra de x+y=k')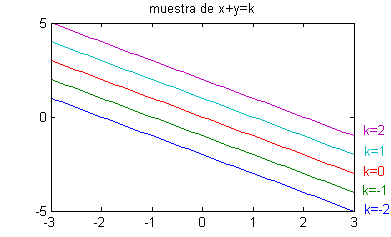
- $x^2+y^2=k$: es la familia de circunferencias de centro $(0,0)$; tomaremos distintos radios, por ejemplo
$$x^2+y^2=1\ ,\ \ x^2+y^2=4\ ,\ \ x^2+y^2=9\ ,\ \ x^2+y^2=16\ ,\ \ x^2+y^2=25$$
t=0:pi/40:2*pi; for k=1:5 x(:,k)= k*cos(t); y(:,k)=k*sin(t); end plot(x,y) title('muestra de x^2+y^2=k^2') axis equal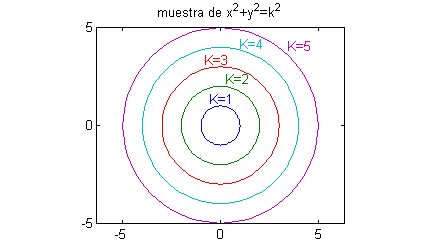
- $y=kx$: es la familia de rectas que pasan por $(0,0)$; podemos dibujar por ejemplo
$$y=-2x\ ,\ \ y=-x\ ,\ \ y=0\ ,\ \ y=x\ ,\ \ y=2x$$
x=-3:.1:3 ; k=-2:2; for n=1:5 y(n,:)=k(n)*x; end plot(x,y) title('muestra de y=kx')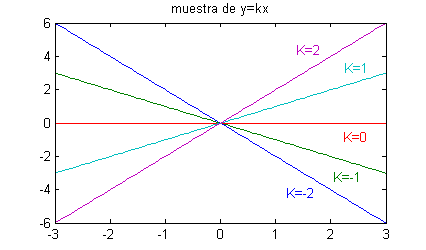
- $x^2+k=y$: es la familia de parábolas paralelas a $y=x^2$; podemos dibujar
$$y=x^2-4\ ,\ \ y=x^2-2\ ,\ \ y=x^2\ ,\ \ y=x^2+2\ ,\ \ y=x^2+4$$
x=-3:.1:3 ; k=-4:2:4; for n=1:5 y(n,:)=k(n)+x.^2; end plot(x,y) title('muestra de y=k+x^2')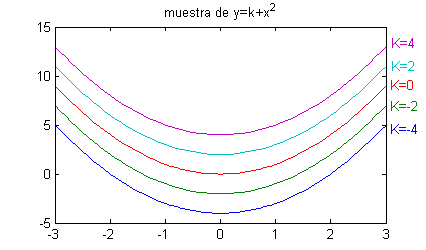
Ejercicio 3
Encuentra una función $z=f(x,y)$ cuyas curvas de nivel sea la familia de curvas indicada. Representa una muestra de las curvas de contorno.
- $x+y=k$
- $x^2+y^2=k$
- $y=kx$
- $x^2+k=y$
Pista
Solución
Recuerda que las curvas de nivel de la superficie $z=f(x,y)$ es la familia de curvas $f(x,y)=k$, variando $k$ en el rango de $f(x,y)$.
-
$x+y=k$ son las curvas de nivel de $z=x+y$:
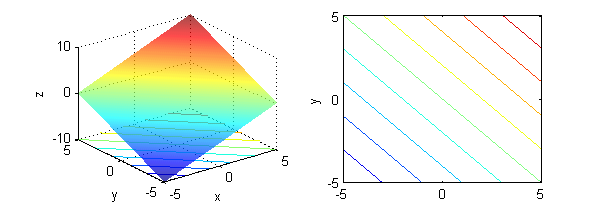
- $x^2+y^2=k$ son las curvas de nivel, por ejemplo, de $z=x^2+y^2$; en este caso, la constante $k$ no puede ser negativa:
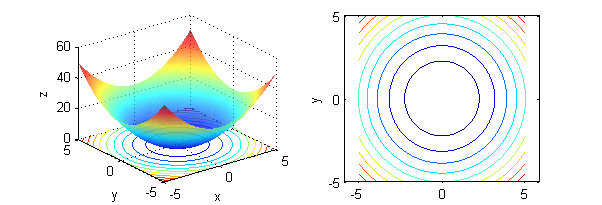
- $y=kx$ son las curvas de nivel de $z=y/x$:
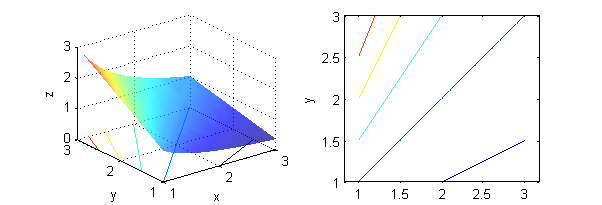
- $x^2+k=y$ son las curvas de nivel de $z=y-x^2$:
Ejercicio 4
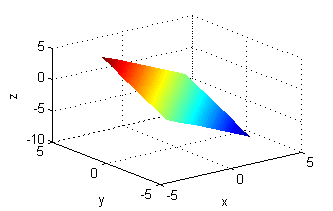
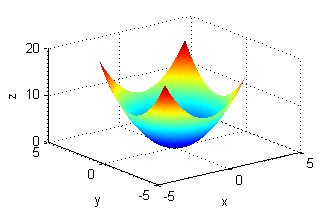
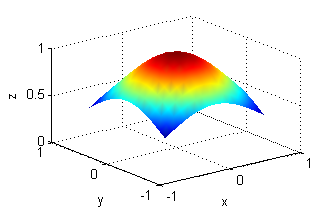
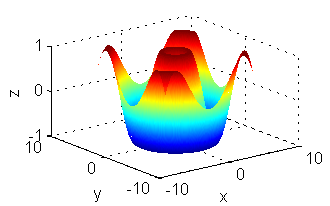
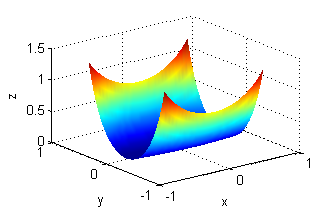
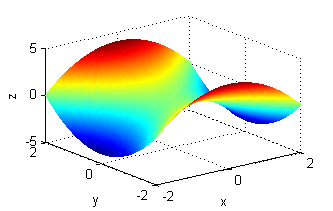
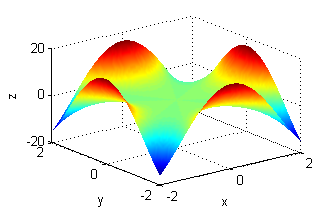
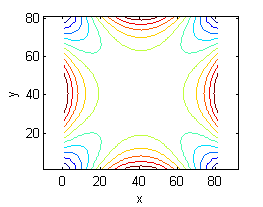
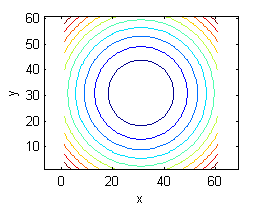
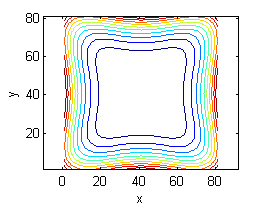
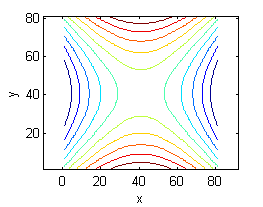
Asocia cada superficie de entre las siguientes con la figura que muestre sus curvas de nivel:
| Superficie a. | Superficie b. |
 |
 |
| Superficie c. | Superficie d. |
 |
 |
| Superficie e. | Superficie f. |
 |
 |
| Superficie g. | Superficie h. |
 |
 |
Curvas de nivel:
| Curvas de nivel 1 | Curvas de nivel 2 |
 |
 |
| Curvas de nivel 3 | Curvas de nivel 4 |
 |
 |
| Curvas de nivel 5 | Curvas de nivel 6 |
 |
 |
| Curvas de nivel 7 | Curvas de nivel 8 |
 |
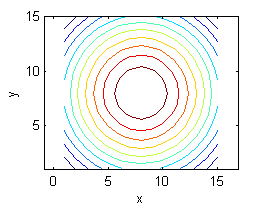 |
Solución
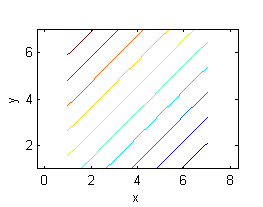
- La superficie a. es $z=-x+y-2$, sus curvas de nivel son las del número 3.
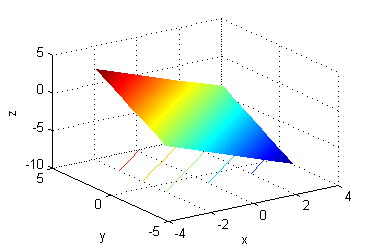
- La superficie es $z=x^2+y^2$, sus curvas de nivel son las del número 5.
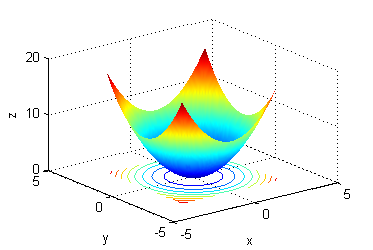
- La superficie es $z=e^{-(x^2+y^2)}$, sus curvas de nivel son las del número 8.
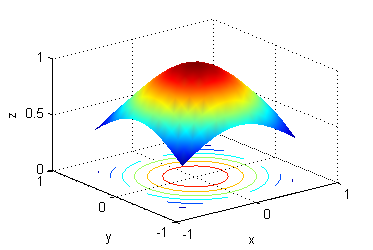
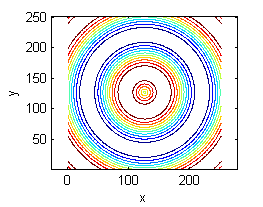
- La superficie es $z=\mbox{sen}\, \sqrt{(x^2+y^2)}$, sus curvas de nivel son las del número 1.
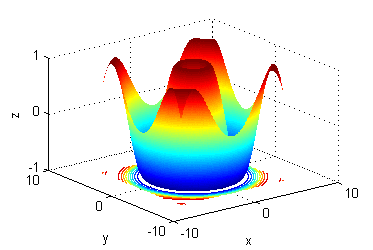
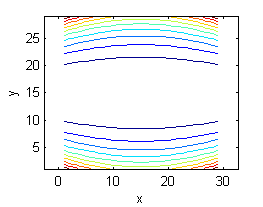
- La superficie es $z=y^2e^{-(x^2+y^2)}$, sus curvas de nivel son las del número 2.
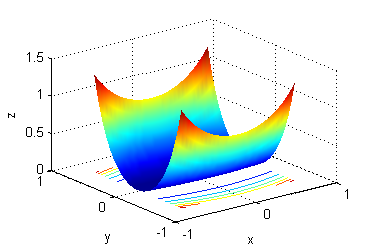
- La superficie es $z=y^2-x^2$, sus curvas de nivel son las del número 7.
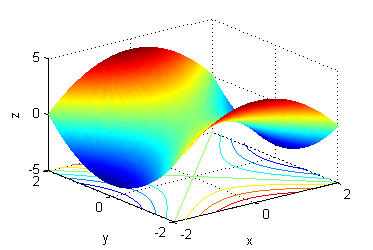
- La superficie es $z=x^4+y^4-3x^2y^2$, sus curvas de nivel son las del número 4.
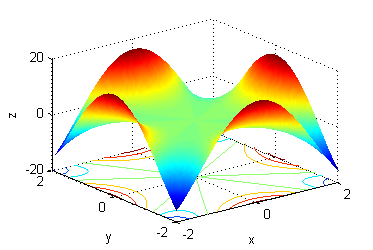
- La superficie es $z=x^4+y^4-x^2y^2$, sus curvas de nivel son las del número 6.
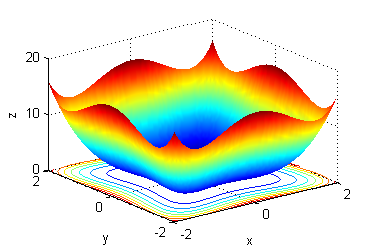
Ejercicio 5
En cada apartado halla la curva de nivel de la superficie que pasa por el punto dado y dibújala:
- $z=x^2+y^2$, punto $P(1,-1)$
- $z=-x^2+y^2$, punto $P(0,2)$
- $z=\sqrt{x^2+y^2}$, punto $P(1,1)$
- $z=\cos(x^2+y^2)$, punto $P\left(\sqrt{\frac{\pi}{4}},\sqrt{\frac{\pi}{4}}\right)$
Pista
Solución
Para encontrar la curva de nivel que pasa por el punto $(x_0,y_0)$, debemos conocer cuál es el valor $z$ correspondiente, es decir, $z_0=f(x_0,y_0)$.
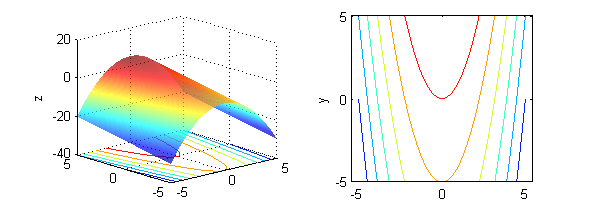
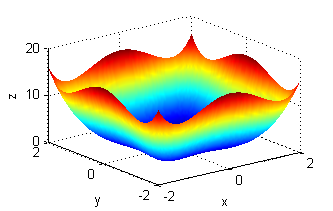
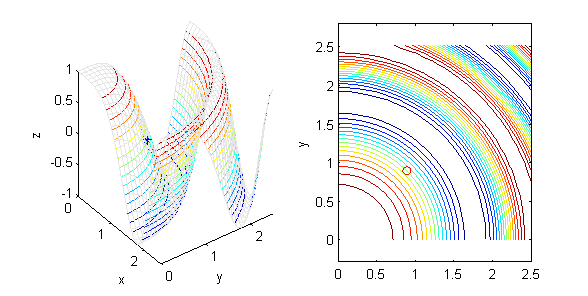
- la curva de nivel de $z=x^2+y^2$ que pasa por el punto $P(1,-1)$ es $x^2+y^2=2$; es una circunferencia, que podemos dibujar a mano muy fácilmente. En el ordenador dibujamos una poción de superficie con unas curvas de contorno (figura de la izquierda) y una muestra de curvas de nivel (figura de la derecha), entre ellas la que se ha determinado en este apartado:
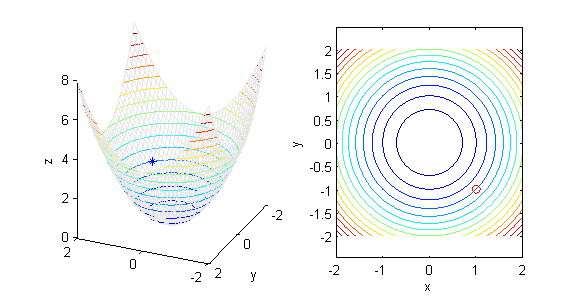
[X,Y]=meshgrid(-2:.1:2); Z=X.^2+Y.^2; subplot(1,2,1) contour3(X,Y,Z,15) surface(X,Y,Z,'EdgeColor',[.9 .9 .9],'FaceColor','none') hold on plot3(1,-1,2,'*') xlabel('x');ylabel('y');zlabel('z'); grid off hold off subplot(1,2,2) contour(X,Y,Z,15) hold on plot(1,-1,'or') xlabel('x');ylabel('y'); hold off axis equal - la curva de nivel de $z=y^2-x^2$ que pasa por el punto $P(0,2)$ es $y^2-x^2=4$, una hipérbola:
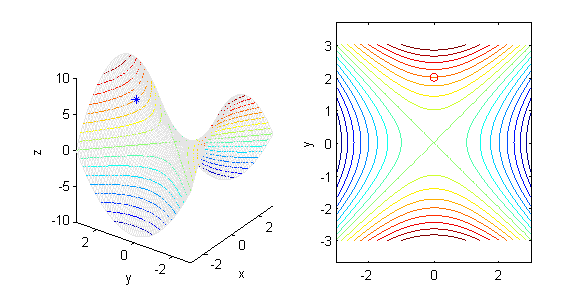
- la curva de nivel de $z=\sqrt{x^2+y^2}$ que pasa por el punto $P(1,1)$ es $x^2+y^2=2$, de nuevo una circunferencia:
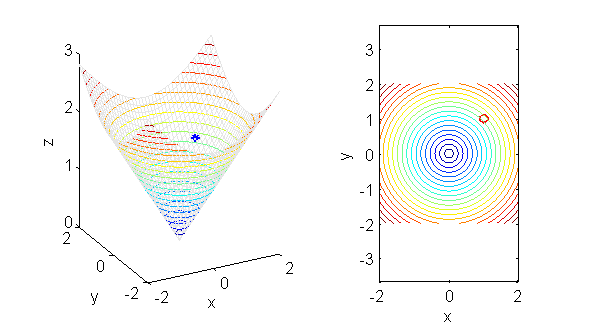
- la curva de nivel de $z=\cos(x^2+y^2)$ que pasa por el punto $P\left(\sqrt{\frac{\pi}{4}},\sqrt{\frac{\pi}{4}}\right)$ es $x^2+y^2=\frac{\pi}{2}$:
Ejercicio 6
En cada apartado halla la curva intersección de la superficie con cada uno de los planos $x=\mbox{cte}$ indicados y dibuja las curvas obtenidas en una misma figura:
- $z=4-x^2-y^2$, planos $x=-3$, $x=-2$, $x=-1$, $x=0$, $x=1$, $x=2$ y $x=3$
- $z=\sqrt{4-x^2-y^2}$, planos $x=-3/2$, $x=-1$, $x=-1/2$, $x=0$, $x=1/2$, $x=1$ y $x=3/2$
- $z=\cos\sqrt{x^2+y^2}$, planos $x=-2$, $x=-1$, $x=0$, $x=1$, y $x=2$
- $z=3(x^2+y^2)e^{-(x^2+y^2)}$, planos $x=-1$, $x=0$, y $x=1$
Ejemplo
Solución
Por ejemplo, la curva intersección de la superficie $z=e^{x+y}$ con el plano $x=1$ es la curva $z=e^{y+1}$ en el plano $x=1$; para dibujarla en el ordenador podemos poner
[X,Y]=meshgrid(1,-1:.1:1); Z=exp(X+Y); plot3(X,Y,Z)Si quisiéramos dibujar las curvas intersección de $z=e^{x+y}$ con los planos $x=-3$, $x=-2$, $x=-1$, $x=0$, $x=1$, $x=2$ y $x=3$, pondríamos
[X,Y]=meshgrid(-3:3,-1:.1:1); Z=exp(X+Y); plot3(X,Y,Z)
- $z=4-x^2-y^2$,
- corte con $x=\pm 3$: $z=-5-y^2$
- corte con $x=\pm 2$: $z=-y^2$
- corte con $x=\pm 1$: $z=3-y^2$
- corte con $x=0$: $z=4-y^2$
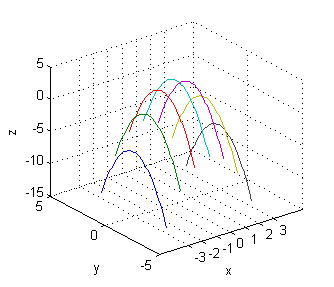
[X,Y]=meshgrid(-3:3,-3:.1:3); Z=4-(X.^2+Y.^2); plot3(X,Y,Z) xlabel('x');ylabel('y');zlabel('z'); set(gca,'XTick',-3:3) grid on - $z=\sqrt{4-x^2-y^2}$,
- corte con $x=\pm 3/2$: $z=\sqrt{\frac{7}{4}-y^2}$
- corte con $x=\pm 1$: $z=\sqrt{3-y^2}$
- corte con $x=\pm 1/2$: $z=\sqrt{\frac{15}{4}-y^2}$
- corte con $x=0$: $z=\sqrt{4-y^2}$
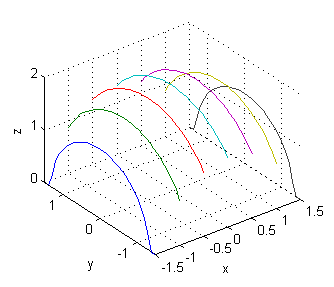
[X,Y]=meshgrid(-3/2:1/2:3/2,-3/2:.1:3/2); Z=sqrt(4-(X.^2+Y.^2)); plot3(X,Y,Z) xlabel('x');ylabel('y');zlabel('z'); set(gca,'XTick',-3/2:1/2:3/2) grid on axis equal - $z=\cos\sqrt{x^2+y^2}$
- corte con $x=\pm 2$: $z=\cos\sqrt{4+y^2}$
- corte con $x=\pm 1$: $z=\cos\sqrt{1+y^2}$
- corte con $x=0$: $z=\cos|y|$
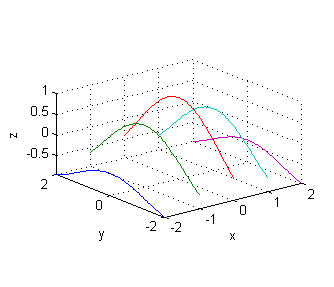
[X,Y]=meshgrid(-2:2,-2:.05:2); Z=cos(sqrt(X.^2+Y.^2)); plot3(X,Y,Z) xlabel('x');ylabel('y');zlabel('z'); set(gca,'XTick',-2:2) grid on axis equal - $z=3(x^2+y^2)e^{-(x^2+y^2)}$
- corte con $x=\pm 1$: $z=3(1+y^2)e^{-(1+y^2)}$
- corte con $x=0$: $z=3y^2e^{-y^2}$
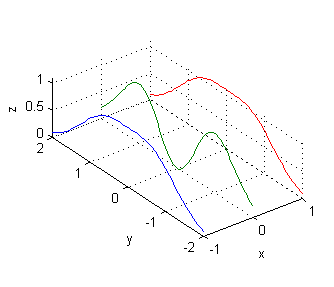
[X,Y]=meshgrid(-1:1,-2:.05:2); Z=3*(X.^2+Y.^2).*exp(-X.^2-Y.^2); plot3(X,Y,Z) xlabel('x');ylabel('y');zlabel('z'); set(gca,'XTick',-1:1) grid on axis equal
Ejercicio 7
En cada apartado halla la curva intersección de la superficie con cada uno de los planos $y=\mbox{cte}$ indicados y dibuja las curvas obtenidas en una misma figura:
- $z=4-2x^2-y^2$, planos $y=-3$, $y=-2$, $y=-1$, $y=0$, $y=1$, $y=2$ e $y=3$
- $z=\sqrt{4-2x^2-y^2}$, planos $y=-3/2$, $y=-1$, $y=-1/2$, $y=0$, $y=1/2$, $y=1$ y $y=3/2$
- $z=4-3x+2y$, planos $y=-3$, $y=-2$, $y=-1$, $y=0$, $y=1$, $y=2$ e $y=3$
- $z=6y^3e^{-(x^2+y^2)}$, planos $y=-2$, $y=-1$, $y=0$, $y=1$, $y=2$
Solución
- $z=4-2x^2-y^2$
- corte con $y=\pm 3$: $z=-5-2x^2$
- corte con $y=\pm 2$: $z=-2x^2$
- corte con $y=\pm 1$: $z=3-2x^2$
- corte con $y=0$: $z=4-2x^2$
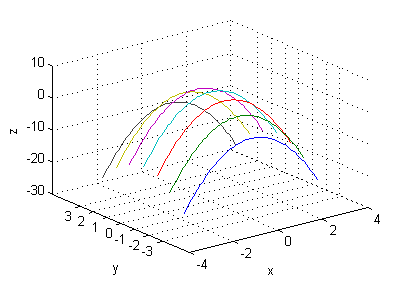
[X,Y]=meshgrid(-3:.1:3,-3:3); Z=4-(2*X.^2+Y.^2); plot3(X',Y',Z') xlabel('x');ylabel('y');zlabel('z'); set(gca,'YTick',-3:3) grid on - $z=\sqrt{4-2x^2-y^2}$
- corte con $y=\pm 3/2$: $z=\sqrt{\frac{7}{4}-2x^2}$
- corte con $y=\pm 1$: $z=\sqrt{3-2x^2}$
- corte con $y=\pm 1/2$: $z=\sqrt{\frac{15}{4}-2x^2}$
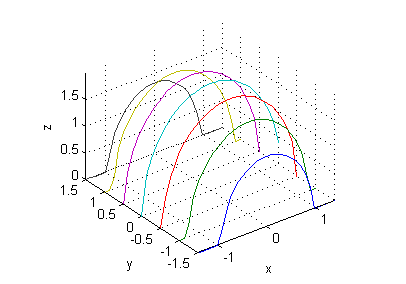
[X,Y]=meshgrid(-sqrt(2):.1:sqrt(2),-3/2:1/2:3/2); Z=sqrt(4-(2*X.^2+Y.^2)); plot3(X',Y',Z') xlabel('x');ylabel('y');zlabel('z'); set(gca,'YTick',-3/2:1/2:3/2) grid on axis equal - $z=4-3x+2y$
- corte con $y=-3$: $z=-2-3x$
- corte con $y=-2$: $z=-3x$
- corte con $y=-1$: $z=2-3x$
- corte con $y=0$: $z=4-3x$
- corte con $y=1$: $z=6-3x$
- corte con $y=2$: $z=8-3x$
- corte con $y=3$: $z=10-3x$
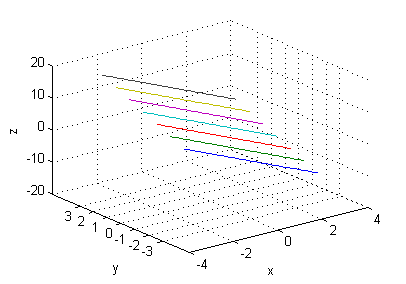
[X,Y]=meshgrid(-3:.1:3,-3:3); Z=4-3*X+2*Y; plot3(X',Y',Z') xlabel('x');ylabel('y');zlabel('z'); set(gca,'YTick',-3:3) grid on - $z=6y^3e^{-(x^2+y^2)}$
- corte con $y=-2$: $z=-48e^{-(x^2+4)}$
- corte con $y=-1$: $z=-6e^{-(x^2+1)}$
- corte con $y=0$: $z=0$
- corte con $y=1$: $z=6e^{-(x^2+1)}$
- corte con $y=2$: $z=48e^{-(x^2+4)}$
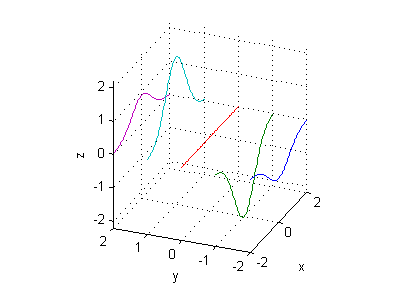
[X,Y]=meshgrid(-2:.05:2,-2:2); Z=6*Y.^3.*exp(-X.^2-Y.^2); plot3(X',Y',Z') xlabel('x');ylabel('y');zlabel('z'); set(gca,'YTick',-2:2) grid on axis equal
Ejercicio 8
En cada apartado se da la ecuación de una superficie, un plano coordenado y un punto. Debes encontrar la curva contenida en la superficie que es paralela al plano y que pasa por el punto:
- superficie: $z=1+x-y$, plano: $XZ$, punto: $P(0,1,0)$
- superficie: $z=1+x-y$, plano: $YZ$, punto: $P(2,0,3)$
- superficie: $z=2+x^2+y^2$, plano: $XZ$, punto: $P(1,1,4)$
- superficie: $z=2+x^2+y^2$, plano: $YZ$, punto: $P(2,0,6)$
- superficie: $z=\sqrt{x^2+y^2-1}$, plano: $XZ$, punto: $P(0,2,\sqrt{3})$
- superficie: $z=\sqrt{x^2+y^2-1}$, plano: $YZ$, punto: $P(1,1,1)$
Solución
- curva dentro de $z=1+x-y$ paralela al plano $XZ$ pasando por el punto $P(0,1,0)$:
$$z=x \ \ \ \mbox{en}\ \ \ y=1$$
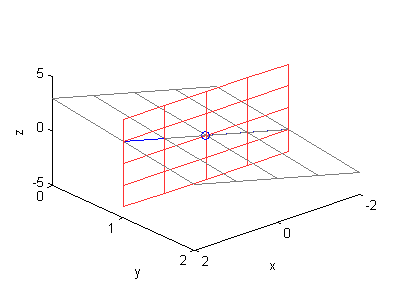
[X,Y]=meshgrid(-2:2,0:2); Z=1+X-Y; surface(X,Y,Z,'EdgeColor',[.5 .5 .5],'FaceColor','none') [X,Y]=meshgrid(-2:2,1); Z=1+X-Y; hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(0,1,0,'o') [X,Z]=meshgrid(-2:2,-4:2:4); surface(X,ones(size(X)),Z,'EdgeColor',[1 .2 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); hold off - curva dentro de $z=1+x-y$ paralela al plano $YZ$ pasando por el punto $P(2,0,3)$:
$$z=3-y \ \ \ \mbox{en}\ \ \ x=2$$
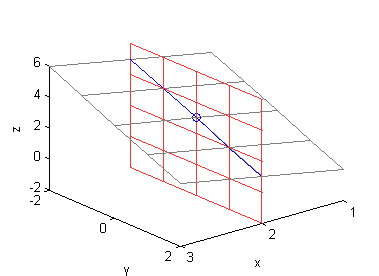
[X,Y]=meshgrid(1:3,-2:2); Z=1+X-Y; surface(X,Y,Z,'EdgeColor',[.5 .5 .5],'FaceColor','none') [X,Y]=meshgrid(2,-2:2); Z=1+X-Y; hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(2,0,3,'o') [Y,Z]=meshgrid(-2:2,-2:2:6); surface(2*ones(size(Y)),Y,Z,'EdgeColor',[1 .2 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); hold off - curva dentro de $z=2+x^2+y^2$ paralela al plano $XZ$ pasando por el punto $P(1,1,4)$:
$$z=3+x^2 \ \ \ \mbox{en}\ \ \ y=1$$
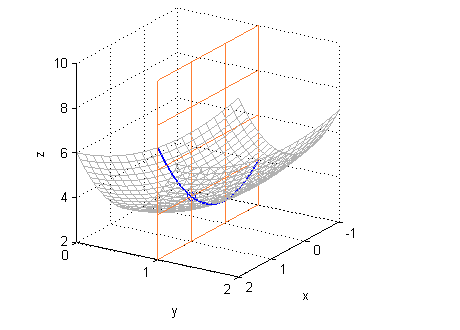
[X,Y]=meshgrid(-1:.1:2,0:.1:2); Z=2+X.^2+Y.^2; surface(X,Y,Z,'EdgeColor',[.7 .7 .7],'FaceColor','none') [X,Y]=meshgrid(-1:.1:2,1); Z=2+X.^2+Y.^2; hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(1,1,4,'o') [X,Z]=meshgrid(-1:2,2:2:10); surface(X,ones(size(X)),Z,'EdgeColor',[1 .5 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); grid on view([150 18]) hold off - curva dentro de $z=2+x^2+y^2$ paralela al plano $YZ$ pasando por el punto $P(2,0,6)$:
$$z=6+y^2 \ \ \ \mbox{en}\ \ \ x=2$$
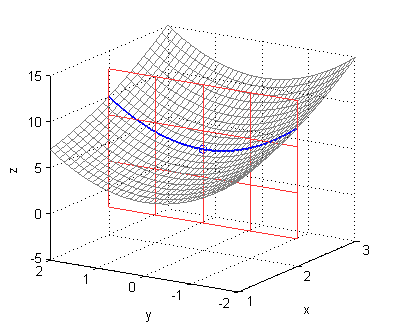
[X,Y]=meshgrid(1:.1:3,-2:.1:2); Z=2+X.^2+Y.^2; surface(X,Y,Z,'EdgeColor',[.5 .5 .5],'FaceColor','none') [X,Y]=meshgrid(2,-2:.1:2); Z=2+X.^2+Y.^2; hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(2,0,6,'o') [Y,Z]=meshgrid(-2:2,-2:5:16); surface(2*ones(size(Y)),Y,Z,'EdgeColor',[1 .2 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); grid on hold off - curva dentro de $z=\sqrt{x^2+y^2-1}$ paralela al plano $XZ$ pasando por el punto $P(0,2,\sqrt{3})$:
$$z=\sqrt{3+x^2} \ \ \ \mbox{en}\ \ \ y=2$$
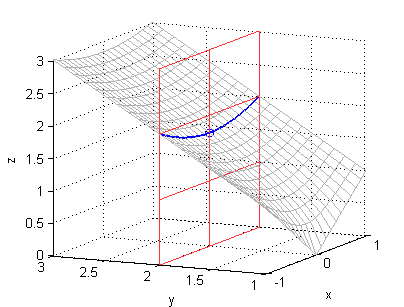
[X,Y]=meshgrid(-1:.1:1,1:.1:3); Z=sqrt(X.^2+Y.^2-1); surface(X,Y,Z,'EdgeColor',[.7 .7 .7],'FaceColor','none') [X,Y]=meshgrid(-1:.1:1,2); Z=sqrt(X.^2+Y.^2-1); hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(0,2,sqrt(3),'o') [X,Z]=meshgrid(-1:1,0:3); surface(X,2*ones(size(X)),Z,'EdgeColor',[1 .2 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); grid on view([150 18]) hold off - curva dentro de $z=\sqrt{x^2+y^2-1}$ paralela al plano $YZ$ pasando por el punto $P(1,1,1)$:
$$z=|y| \ \ \ \mbox{en}\ \ \ x=1$$
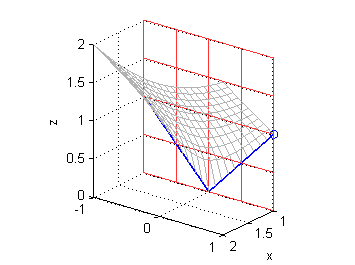
[X,Y]=meshgrid(1:.1:2,-1:.1:1); Z=sqrt(X.^2+Y.^2-1); surface(X,Y,Z,'EdgeColor',[.7 .7 .7],'FaceColor','none') [X,Y]=meshgrid(1,-1:.1:1); Z=sqrt(X.^2+Y.^2-1); hold on plot3(X,Y,Z,'LineWidth',1.2) plot3(1,1,1,'o') [Y,Z]=meshgrid(-1:.5:1,0:.5:2); surface(ones(size(Y)),Y,Z,'EdgeColor',[1 .2 .2],'FaceColor','none') xlabel('x');ylabel('y');zlabel('z'); grid on view([151 32]) axis equal hold off
Ejercicio 9
Halla el gradiente de las siguientes funciones
- $f(x,y)=xy^2-3x^2$
- $f(x,y)=x\mbox{sen}\, (xy)$
- $f(x,y)=2-\frac{y}{x+y}$
Definición
Solución
El gradiente de $z=f(x,y)$ es $$\nabla f(x,y)=(f'_x(x,y),f'_y(x,y))$$
- $\nabla f(x,y)=\nabla(xy^2-3x^2)=(y^2-6x,2xy)$
- $\nabla f(x,y)=\nabla(x\,\mbox{sen}\, (xy))=(\mbox{sen}\, (xy)+xy\cos(xy), x^2\cos(xy))$
- $\nabla f(x,y)=\nabla(\sqrt{x^2+y^2})=(\frac{x}{\sqrt{x^2+y^2}}, \frac{y}{\sqrt{x^2+y^2}})$
- $\nabla f(x,y)=\nabla(2-\frac{y}{x+y})=(\frac{-y}{(x+y)^2}, \frac{-x}{(x+y)^2})$
Ejercicio 10
Encuentra las derivadas parciales segundas de las funciones
- $f(x,y)=xy^2-3x^2$
- $f(x,y)=x\mbox{sen}\, (xy)$
Solución
- $f(x,y)=xy^2-3x^2$: $$f''_{xx}=-6$$ $$f''_{xy}=2y$$ $$f''_{yy}=2x$$
- $f(x,y)=x\mbox{sen}\, (xy)$: $$f''_{xx}=2y\cos(xy)-xy^2\mbox{sen}(xy)$$ $$f''_{xy}=2x\cos(xy)-x^2y\mbox{sen}(xy)$$ $$f''_{yy}=-x^3\mbox{sen}(xy)$$
Ejercicio 11
Una partícula, A, se desplaza por la superficie $f(x,y)=(x-1)^2+y^2$ paralelamente al plano $XZ$. Otra partícula, B, se desplaza de la misma manera pero por la superficie $g(x,y)=(x^2+y^2)/2$. Cuando pasan por el punto $P(1,1,1)$, ¿cuál gana antes altura?
Pista
Solución
Recuerda que la derivada parcial de $f(x,y)$ respecto de $x$ en $(a,b)$,
es decir, $f'_x(a,b)$ es la derivada en $x=a$ de la curva intersección de $z=f(x,y)$ con el plano $y=b$.
La partícula B, ya que $g'_x(1,1)>f'_x(1,1)$. En la figura vemos la trayectoria de la partícula A en verde y la de la B en rosa:
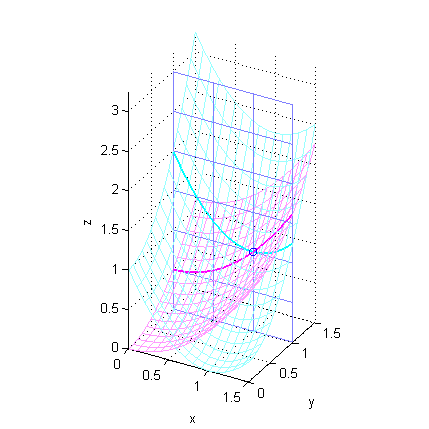

[X,Y]=meshgrid(0:.1:1.5);
Z=(X-1).^2+Y.^2;
surface(X,Y,Z,'EdgeColor',[0.6 1 1],'FaceColor','none')
hold on
Z=(X.^2+Y.^2)/2;
surface(X,Y,Z,'EdgeColor',[1 .6 1],'FaceColor','none')
[X,Y]=meshgrid(0:.1:1.5,1);
Z=(X-1).^2+Y.^2;
plot3(X,Y,Z,'c','LineWidth',1.2)
Z=(X.^2+Y.^2)/2;
plot3(X,Y,Z,'m','LineWidth',1.2)
plot3(1,1,1,'o')
[X,Z]=meshgrid(0:.5:1.5,0:.5:3);
surface(X,ones(size(X)),Z,'EdgeColor',[0.5 0.5 1],'FaceColor','none')
xlabel('x');ylabel('y');zlabel('z');
grid on
view([29 30])
axis equal
hold off
Ejercicio 12
Los curvas corte de las superficies $z=f(x,y)$, $z=g(x,y)$ y $z=h(x,y)$ con el plano $x=2$ son la azul, la verde y la roja respectivamente:
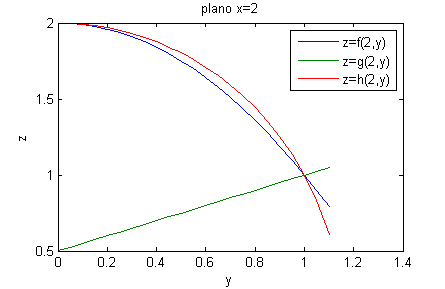
Ordena de menor a mayor los números

Ordena de menor a mayor los números
- $f'_y(2,1)$, $g'_y(2,1)$ y $h'_y(2,1)$
- $|f'_y(2,1)|$, $|g'_y(2,1)|$ y $|h'_y(2,1)|$
Pista
Solución
Recuerda que la derivada parcial de $f(x,y)$ respecto de $y$ en $(a,b)$,
es decir, $f'_y(a,b)$, es la derivada en $y=b$ de la curva intersección de $z=f(x,y)$ con el plano $x=a$.
Por las pendientes de estas curvas en el punto $(2,1)$ deducimos que
$$h'_y(2,1)<f'_y(2,1)<g'_y(2,1)$$
y
$$|g'_y(2,1)|<|f'_y(2,1)|<|h'_y(2,1)|$$
Ejercicio 13
Indica si los vectores siguientes son o no direcciones. Calcula la dirección correspondiente al que no lo sea y en todos los casos escribe las direcciones de la forma $(\cos \varphi,\mbox{sen}\, \varphi)$.
- ${\bf v}=(1,1)$
- ${\bf v}=(1,0)$
- ${\bf v}=(0,-1)$
- ${\bf v}=(-\sqrt{3},1)$
- ${\bf v}=(-1,-\sqrt{3})$
Definición
Solución
Un vector ${\bf u}$ del plano es una dirección si es de norma 1 y se podrá expresar como ${\bf u}=(\cos \varphi,\mbox{sen}\, \varphi)$, siendo $\varphi$ el ángulo que forma el vector ${\bf u}$ con el eje 0X positivo.
- ${\bf v}=(1,1)$ no es dirección; su dirección es $${\bf u}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})=(\cos \frac{\pi}{4}, \mbox{sen}\, \frac{\pi}{4})$$
- ${\bf v}=(1,0)$ es una dirección; $${\bf v}=(1,0)=(\cos 0, \mbox{sen}\, 0)$$
- ${\bf v}=(0,-1)$ es una dirección; $${\bf v}=(0,-1)=(\cos \frac{3\pi}{2}, \mbox{sen}\, \frac{3\pi}{2})$$
- ${\bf v}=(-\sqrt{3},1)$ no es dirección; su dirección es $${\bf u}=(\frac{-\sqrt{3}}{2},\frac{1}{2})=(\cos \frac{5\pi}{6}, \mbox{sen}\, \frac{5\pi}{6})$$
- ${\bf v}=(-1,-\sqrt{3})$ no es dirección; su dirección es $${\bf u}=(\frac{-1}{2},\frac{-\sqrt{3}}{2})=(\cos \frac{4\pi}{3}, \mbox{sen}\, \frac{4\pi}{3})$$
Ejercicio 14
Representa los vectores de módulos $r_1=2$, $r_2=3$ y $r_3=4$ correspondientes a cada dirección:
- $\varphi=\frac{\pi}{5}$
- $\varphi=\frac{11\pi}{12}$
- $\varphi=\frac{7\pi}{6}$
Pista
Solución
Si la dirección nos viene dada por $\varphi$, el ángulo que forma el vector ${\bf u}$ con el eje 0X positivo, el vector de norma 1 es ${\bf u}=(\cos \varphi,\mbox{sen}\, \varphi)$.
Para dibujarlos en el ordenador todos a la vez, podemos poner
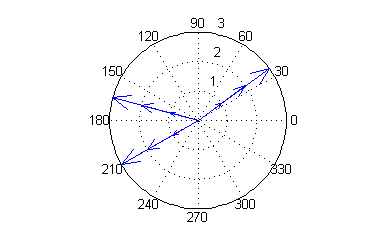
a=[pi/5 11*pi/12 7*pi/6]; compass([2*cos(a) 3*cos(a) 4*cos(a)], [2*sin(a) 3*sin(a) 4*sin(a)])

Ejercicio 15
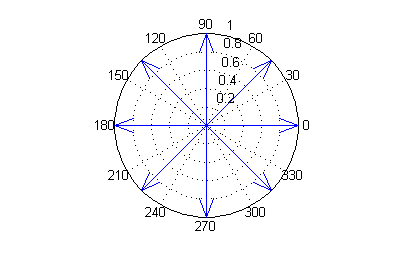
Escribe y representa las direcciones correspondientes a los 8 puntos cardinales siguientes: Norte, Noreste, Este, Sureste, Sur, Suroeste, Oeste, Noroeste.
Solución
| Norte: $(0,1)$ | ||||
| Noroeste: $(\frac{-\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ | Noreste: $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ | |||
| Oeste: $(-1,0)$ | Este: $(1,0)$ | |||
| Suroeste: $(\frac{-\sqrt{2}}{2},\frac{-\sqrt{2}}{2})$ | Sureste:$(\frac{\sqrt{2}}{2},\frac{-\sqrt{2}}{2})$ | |||
| Sur: $(0,-1)$ |
angulos=0:pi/4:7*pi/4; compass(cos(angulos),sin(angulos))o bien
angulos=0:pi/4:7*pi/4; [x,y]=pol2cart(angulos,ones(1,8)); % transforma coordenadas polares a cartesianas compass(x,y)
Ejercicio 16
Sabiendo que $\nabla f(x,y)=(2xy,x^2)$, ordena las derivadas direccionales de $z=f(x,y)$ en el punto $P(-1,-1)$ correspondientes a las 8 direcciones N, NE, E, SE, S, SW, W, NW. Puedes denotarlas como $D_N$, $D_{NE}$, $\ldots$
Pista
Solución
Recuerda que si una función $f(x,y)$ es diferenciable, la derivada direccional en la dirección ${\bf u}$ es el producto escalar de $\nabla f(x,y)$ por la dirección ${\bf u}$.
$$D_N=1,\ D_{NE}=\frac{3}{2}\sqrt{2},\ D_E=2,\ D_{SE}=\frac{\sqrt{2}}{2},\ D_S=-1,\ D_{SW}=\frac{-3}{2}\sqrt{2},\ D_W=-2,\ D_{NW}=\frac{-\sqrt{2}}{2}$$
por tanto
$$D_{SW}<D_W<D_S<D_{NW}<D_{SE}<D_N<D_E<D_{NE}$$
Para calcularlas en el ordenador,
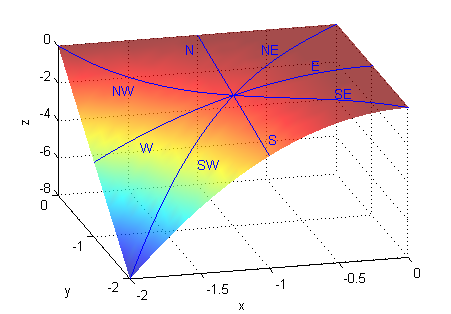
angulos=0:pi/4:7*pi/4; [x,y]=pol2cart(angulos,ones(1,8)); sym([2,1]*[x;y])En la siguiente figura puedes ver una porción de la superficie $f(x,y)=x^2y$, cuyo gradiente es $(2xy,x^2)$ y las curvas, en azul, intersección de la superficie con los planos verticales en las direcciones en las que se han calculado las derivadas direccionales:

Ejercicio 17
Verdadero o falso:
- Toda función diferenciable es continua.
- Toda función continua es diferenciable.
- Si $f'_x$ no es continua, entonces $f$ no es diferenciable.
- Si $f$ es continua pero no diferenciable, entonces tanto $f'_x$ como $f'_y$ son no continuas.
Solución
- Verdadero.
- Falso, una función puede ser continua y no diferenciable.
- Falso, no es necesario que las parciales sean continuas para que la función sea diferenciable.
- Verdadero, puesto que si una (o las dos) parciales fuera continua, entonces la función sería diferenciable.
Ejercicio 18
En cada caso, halla dos vectores tangentes a la superficie en el punto que la acompaña, que no sean paralelos. Después, representa la superficie y los vectores con el ordenador.
- superficie: $z=\sqrt{4-x^2-y^2}$; punto: $P(1,1,\sqrt{2})$
- superficie: $z=-\sqrt{x^2+y^2}$; punto: $P(0,1,-1)$
- superficie: $z=3y^2$; punto: $P(1,-1,3)$
- superficie: $z=2-x^3$; punto: $P(\frac{1}{2},0,\frac{15}{8})$
Pista
Solución
Dos vectores tangentes a la superficie $z=f(x,y)$ en el punto $(a,b,f(a,b))$ son $${\bf u}=(1,0,f'_x(a,b))\ \ , \ \ {\bf v}=(0,1,f'_y(a,b))$$
- dos vectores tangentes a la superficie $z=\sqrt{4-x^2-y^2}$ en el punto $P(1,1,\sqrt{2})$ son
$${\bf u}=(1,0,\frac{-1}{\sqrt{2}})\ \ , \ \ {\bf v}=(0,1,\frac{-1}{\sqrt{2}})$$
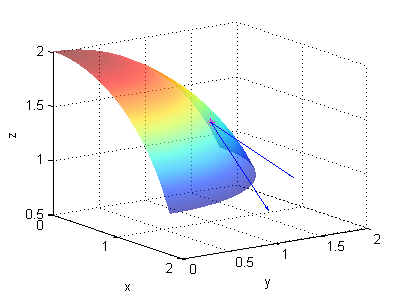
[R,T]=meshgrid(0:.1:1.8,0:pi/20:pi/2); Z=sqrt(4-R.^2); surface(R.*cos(T),R.*sin(T),Z) shading interp alpha(.6) hold on plot3(1,1,sqrt(2),'*m') quiver3([1 1],[1,1],[sqrt(2) sqrt(2)],[1 0],[0 1],[-1/sqrt(2) -1/sqrt(2)]) xlabel('x');ylabel('y');zlabel('z'); view([55 18]) grid on hold off - dos vectores tangentes a la superficie $z=-\sqrt{x^2+y^2}$ en el punto $P(0,1,-1)$ son
$${\bf u}=(1,0,0)\ \ , \ \ {\bf v}=(0,1,-1)$$
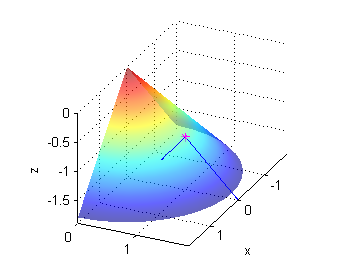
[R,T]=meshgrid(0:.1:1.8,0:pi/20:pi); Z=-R; surface(R.*cos(T),R.*sin(T),Z) shading interp alpha(.6) hold on plot3(0,1,-1,'*m') quiver3([0 0],[1,1],[-1 -1],[1 0],[0 1],[0 -1]) xlabel('x');ylabel('y');zlabel('z'); view([115 26]) axis equal grid on hold off - dos vectores tangentes a la superficie $z=3y^2$ en el punto $P(1,-1,3)$ son
$${\bf u}=(1,0,0)\ \ , \ \ {\bf v}=(0,1,-6)$$
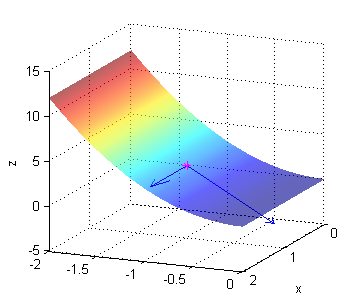
[X,Y]=meshgrid(0:.1:2,-2:.1:0); Z=3*Y.^2; surface(X,Y,Z) shading interp alpha(.6) hold on plot3(1,-1,3,'*m') quiver3([1 1],[-1,-1],[3 3],[1 0],[0 1],[0 -6]) xlabel('x');ylabel('y');zlabel('z'); view([113 16]) grid on hold off - dos vectores tangentes a la superficie $z=2-x^3$ en el punto $P(\frac{1}{2},0,\frac{15}{8})$ son
$${\bf u}=(1,0,\frac{-3}{4})\ \ , \ \ {\bf v}=(0,1,0)$$
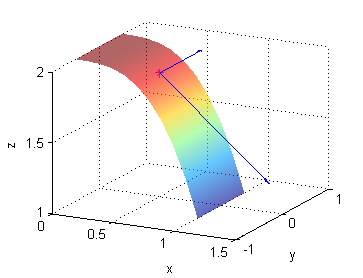
[X,Y]=meshgrid(0:.1:1,-.5:.1:.5); Z=2-X.^3; surface(X,Y,Z) shading interp alpha(.6) hold on plot3(.5,0,15/8,'*m') quiver3([.5 .5],[0 0],[15/8 15/8],[1 0],[0 1],[-3/4 0]) xlabel('x');ylabel('y');zlabel('z'); view([55 18]) grid on hold off
Ejercicio 19
En cada caso, halla dos vectores tangentes a la superficie en el punto que la acompaña, que no sean paralelos. Después, representa la superficie y los vectores con el ordenador.
- superficie: $y=2-x^2$; punto: $P(1,1,2)$
- superficie: $y=\sqrt{9-x^2}$; punto: $P(2,\sqrt{5},2)$
- superficie: $x=z\cos y$; punto: $P(0,\frac{\pi}{2},2)$
- superficie: $x=e^{-y}$; punto: $P(1,0,-1)$
Pista
Solución
- Dos vectores tangentes a la superficie $y=g(x,z)$ en el punto $(a,g(a,c),c)$ son $${\bf u}=(1,g'_x(a,c),0)\ \ , \ \ {\bf v}=(0,g'_z(a,c),1)$$
- Dos vectores tangentes a la superficie $x=h(y,z)$ en el punto $(h(b,c),b,c)$ son $${\bf u}=(h'_y(b,c),1,0)\ \ , \ \ {\bf v}=(h'_z(b,c),0,1)$$
- dos vectores tangentes a la superficie $y=2-x^2$ en el punto $P(1,1,2)$ son
$${\bf u}=(1,-2,0)\ \ , \ \ {\bf v}=(0,0,1)$$
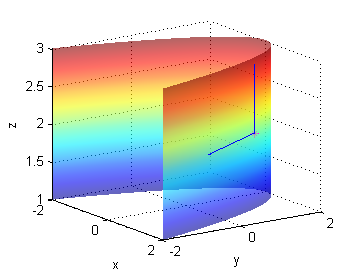
[X,Z]=meshgrid(-2:.1:2,1:.1:3); Y=2-X.^2; surface(X,Y,Z) shading interp alpha(.6) hold on plot3(1,1,2,'*m') quiver3([1 1],[1 1],[2 2],[1 0],[-2 0],[0 1]) xlabel('x');ylabel('y');zlabel('z'); view([55 18]) grid on hold off - dos vectores tangentes a la superficie $y=\sqrt{9-x^2}$ en el punto $P(2,\sqrt{5},2)$ son
$${\bf u}=(1,\frac{-2}{\sqrt{5}},0)\ \ , \ \ {\bf v}=(0,0,1)$$
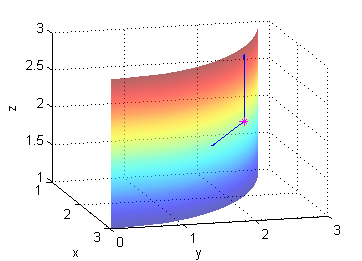
[X,Z]=meshgrid(1:.1:3); Y=sqrt(9-X.^2); surface(X,Y,Z) shading interp alpha(.6) hold on plot3(2,sqrt(5),2,'*m') quiver3(2*[1 1],sqrt(5)*[1 1],2*[1 1],[1 0],[-2/sqrt(5) 0],[0 1]) xlabel('x');ylabel('y');zlabel('z'); view([75 18]) grid on hold off - dos vectores tangentes a la superficie $x=z\cos y$ en el punto $P(0,\frac{\pi}{2},2)$ son
$${\bf u}=(-2,1,0)\ \ , \ \ {\bf v}=(0,0,1)$$
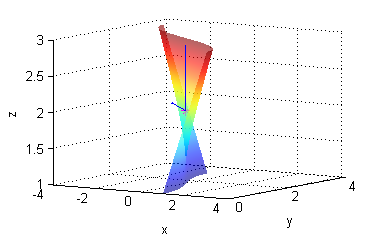
[Y,Z]=meshgrid(0:.1:pi,1:.1:3); X=Z.*cos(Y); surface(X,Y,Z) shading interp alpha(.6) hold on plot3(0,pi/2,2,'*m') quiver3([0 0],(pi/2)*[1 1],[2 2],[-2 0],[1 0],[0 1]) xlabel('x');ylabel('y');zlabel('z'); view([33 10]) grid on hold off - dos vectores tangentes a la superficie $x=e^{-y}$ en el punto $P(1,0,-1)$ son
$${\bf u}=(\frac{1}{2},1,0)\ \ , \ \ {\bf v}=(\frac{1}{2},0,1)$$
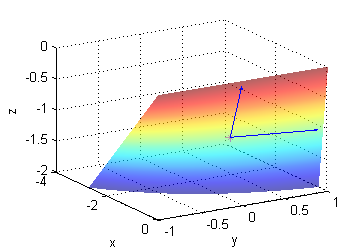
[Y,Z]=meshgrid(-1:.1:1,-2:.1:0); X=Z.*exp(-Y)/2; surface(X,Y,Z) shading interp alpha(.6) hold on plot3(-.5,0,-1,'*m') quiver3(-.5*[1 1],[0 0],-[1 1],.5*[1 1],[1 0],[0 1]) xlabel('x');ylabel('y');zlabel('z'); view([59 24]) grid on hold off
Ejercicio 20
Elige de entre los siguientes aquellos vectores que sean perpendiculares a la curva $x^2+4y^2=1$ en el punto $P(\frac{\sqrt{3}}{2},\frac{-1}{4})$. Representa un arco de la curva que contenga al punto $P$ y todos los vectores, a mano y en el ordenador.
$${\bf u_1}=(\sqrt{3},2)\ \ , \ \ {\bf u_2}=(\sqrt{3},-2)\ \ , \ \ {\bf u_3}=(-3,1)\ \ , \ \ {\bf u_4}=(\frac{-\sqrt{3}}{2},1)\ \ , \ \ {\bf u_5}=(1,-\sqrt{3})$$
Pista
Solución
Una manera rápida de buscar cuáles son perpendiculares a la curva en ese punto es hallar la pendiente que tiene la curva en ese punto.
La pendiente de la curva en el punto $P$ es $\frac{-2}{\sqrt{3}}$, luego son perpendiculares
$${\bf u_2}=(\sqrt{3},-2) \ \ \mbox{y}\ \ {\bf u_4}=(\frac{-\sqrt{3}}{2},1)$$
Para representarlos en el ordenador podemos escribir
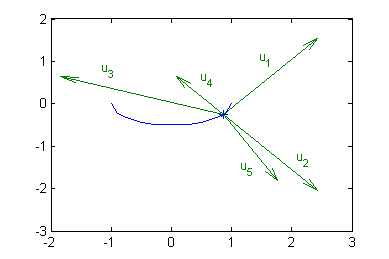
x=-1:.1:1; y=-sqrt(1-x.^2)/2; plot(x,y) % arco de la curva hold on a=sqrt(3)/2; plot(a,-1/4,'*') % punto quiver(a*ones(1,5),-ones(1,5)/4,[2*a 2*a -3 -a 1],[2 -2 1 1 -2*a]) % los cinco vectores hold off

Ejercicio 21
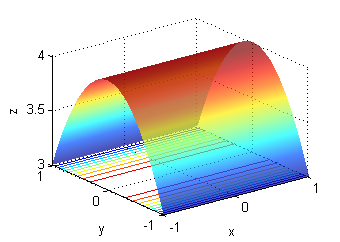
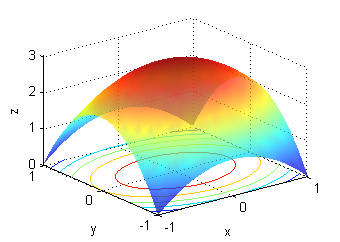
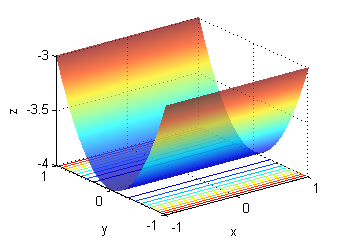
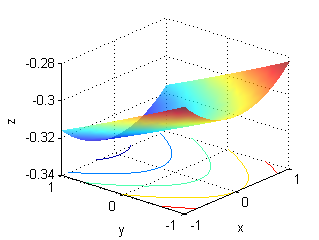
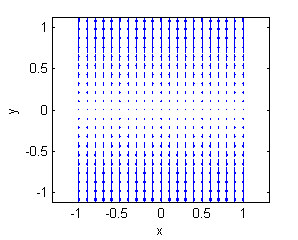
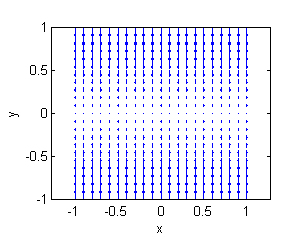
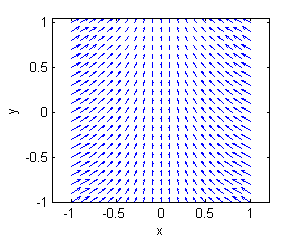
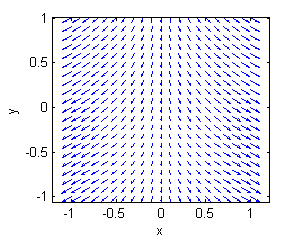
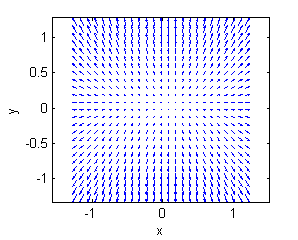
Asocia cada superficie con la muestra de su gradiente:
| Superficie a. | Superficie b. |
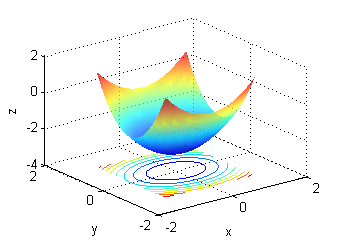
 |
 |
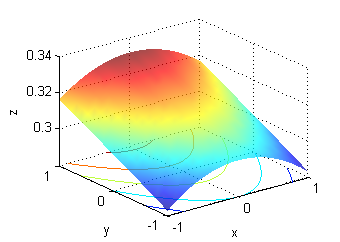
| Superficie c. | Superficie d. |
 |
 |
| Superficie e. | Superficie f. |
 |
 |
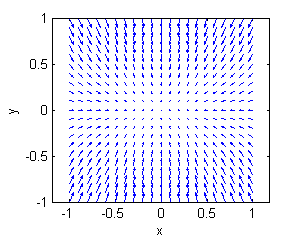
Muestras de gradientes:
| Gradiente 1. | Gradiente 2. |
 |
 |
| Gradiente 3. | Gradiente 4. |
 |
 |
| Gradiente 5. | Gradiente 6. |
 |
 |
Pista
Solución
Recuerda que
- el vector gradiente es perpendicular a la curva de nivel que pasa por el punto donde ese gradiente se calcula,
- el vector gradiente indica el sentido de crecimiento
- La superficie a. es una porción de $z=4-y^2$, su gradiente está representado en la figura llamada ''Gradiente 3'':
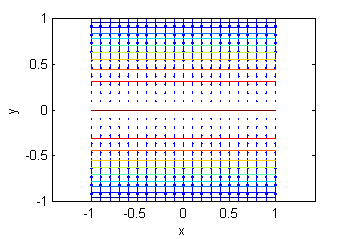
- La superficie b. es una porción de $z=-3+x^2+2y^2$, su gradiente está representado en la figura llamada ''Gradiente 6'':
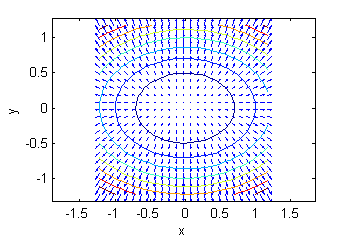
- La superficie c. es una porción de $10z=\sqrt{10+y-x^2}$, su gradiente está representado en la figura llamada ''Gradiente 4'':
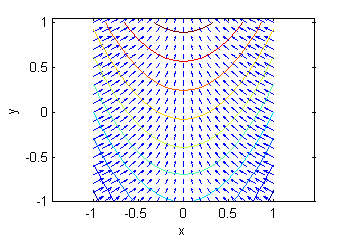
- La superficie d. es una porción de $z=3-x^2-2y^2$, su gradiente está representado en la figura llamada ''Gradiente 1'':
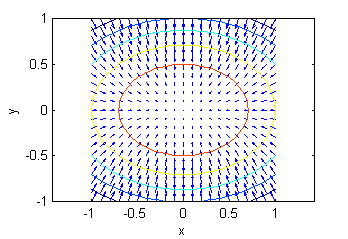
- La superficie e. es una porción de $z=y^2-4$, su gradiente está representado en la figura llamada ''Gradiente 2'':
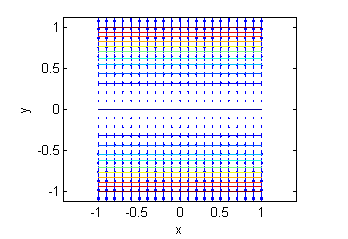
- La superficie f. es una porción de $10z=-\sqrt{10+y-x^2}$, su gradiente está representado en la figura llamada ''Gradiente 5'':
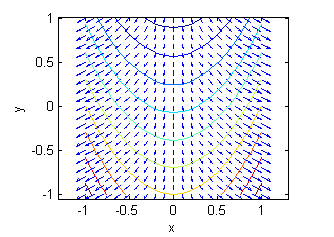
Ejercicio 22
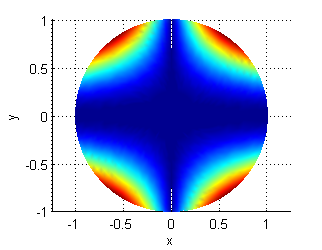
Cada punto $(x,y)$ del disco $D=\{(x,y)/\, x^2+y^2\leq 1\}$ está a una temperatura igual a $T(x,y)=|x| y^2$. Halla
- los puntos frontera de $D$;
- los puntos singulares de la función $T(x,y)$ en $D$;
- los puntos estacionarios de la función $T(x,y)$ en $D$.
Solución
- los puntos frontera de $D$ son los puntos de la circunferencia $x^2+y^2=1$;
- los puntos singulares de la función $T(x,y)$ en $D$ son todos los de la forma $(0,y)$ con $-1\leq y\leq 1$;
- los puntos estacionarios de la función $T(x,y)$ en $D$ son todos los de la forma $(x,0)$ con $-1\leq x\leq 1$, $x\neq 0$.
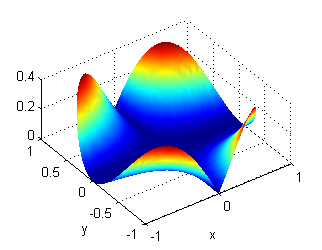
[R,T]=meshgrid(0:.05:1,0:pi/50:2*pi);
surf(R.*cos(T),R.*sin(T),R.^3.*abs(cos(T)).*sin(T).^2)
shading interp
xlabel('x');ylabel('y')
La figura anterior muestra la función temperatura en los puntos de $D$. Si lo que queremos es dibujar la placa coloreada según su temperatura, basta que veamos la gráfica anterior desde arriba; para ello añadimos al código anterior las líneas
view([0,90]) axis equal