Enunciado
Dada la función $f\left( {x,y} \right) = \frac{1}{100} e^{x^2 - 2x + y^2} + 30$, se pide
- Encontrar y clasificar los puntos críticos de $f$.
- Calcular los extremos de $f$ en la región del plano cerrada y acotada $D = \left\{ {\left( {x,y} \right) \in {R^2}/{x^2} + {y^2} \le 4} \right\}$.
Representación de la función
El dominio $D$, en el que tenemos que calcular los valores máximos y mínimos de la función $f$, es el círculo de centro (0,0) y radio 2.
La figura siguiente representa la gráfica de la función $f$, la frontera $C$ del dominio $D$ (curva en azul del plano $z=0$) y la curva imagen de $C$ por $f$ (curva en color naranja).
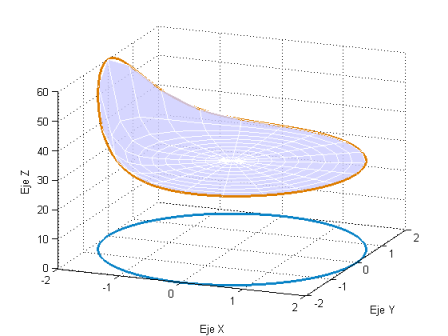
La figura siguiente representa la gráfica de la función $f$, la frontera $C$ del dominio $D$ (curva en azul del plano $z=0$) y la curva imagen de $C$ por $f$ (curva en color naranja).

Apartado a
Como la función $f$ es diferenciable, los puntos críticos de la función en su dominio, $R^2$, serán los que cumplan $$f_x^' = {{\left( {x - 1} \right)} \over {50}}{e^{{x^2} - 2x + {y^2}}} = 0\,\,\,\,\,\,\,\,\,\,f_y^' = {y \over {50}}\,\,{e^{{x^2} - 2x + {y^2}}} = 0$$Resuelve este sistema y, en cuanto lo tengas, pulsa sobre el botón
Como la función exponencial nunca se anula, las dos derivadas parciales se anularán si $x=1$, $y=0$. El único punto crítico es entonces el punto $\left( {1,\,\,0} \right)$.
Como la función exponencial es creciente y además $${e^{{x^2} - 2x + {y^2}}} = {e^{{{\left( {x - 1} \right)}^2} + {y^2} - 1}}$$ el punto $\left( {1,\,\,0} \right)$ será mínimo.
No obstante, podemos utilizar también el método del hessiano para analizar qué tipo de extremo es. Teniendo en cuenta que: $$f_{xx}^{''} = {1 \over {50}}{e^{{x^2} - 2x + {y^2}}} + {1 \over {25}}\left( {x - 1} \right)^2{e^{{x^2} - 2x + {y^2}}}$$ $$f_{xy}^{''} = {1 \over {25}}y\left( {x - 1} \right){e^{{x^2} - 2x + {y^2}}}$$ $$f_{yy}^{''} = {1 \over {50}}{e^{{x^2} - 2x + {y^2}}} + {1 \over {25}}{y^2}{e^{{x^2} - 2x + {y^2}}}$$ resultaría $$H\left( {1,\,\,\,0} \right) = {1 \over {50}}\left| {\matrix{{{e^{ - 1}}} & 0 \cr 0 & {{e^{ - 1}}} \cr } } \right| > 0\,\,\,\,\,\,\,\,f_{xx}^{''}\left( {1,0} \right) = {1 \over {50}}{e^{ - 1}} > 0$$ que permitiría concluir igualmente que la función $f$ tiene un mínimo relativo en el punto $\left( {1,\,\,0} \right)$ con valor $f\left( {1,\,0} \right) = {1 \over {100}}{e^{ - 1}} + 30$.
Como la función exponencial es creciente y además $${e^{{x^2} - 2x + {y^2}}} = {e^{{{\left( {x - 1} \right)}^2} + {y^2} - 1}}$$ el punto $\left( {1,\,\,0} \right)$ será mínimo.
No obstante, podemos utilizar también el método del hessiano para analizar qué tipo de extremo es. Teniendo en cuenta que: $$f_{xx}^{''} = {1 \over {50}}{e^{{x^2} - 2x + {y^2}}} + {1 \over {25}}\left( {x - 1} \right)^2{e^{{x^2} - 2x + {y^2}}}$$ $$f_{xy}^{''} = {1 \over {25}}y\left( {x - 1} \right){e^{{x^2} - 2x + {y^2}}}$$ $$f_{yy}^{''} = {1 \over {50}}{e^{{x^2} - 2x + {y^2}}} + {1 \over {25}}{y^2}{e^{{x^2} - 2x + {y^2}}}$$ resultaría $$H\left( {1,\,\,\,0} \right) = {1 \over {50}}\left| {\matrix{{{e^{ - 1}}} & 0 \cr 0 & {{e^{ - 1}}} \cr } } \right| > 0\,\,\,\,\,\,\,\,f_{xx}^{''}\left( {1,0} \right) = {1 \over {50}}{e^{ - 1}} > 0$$ que permitiría concluir igualmente que la función $f$ tiene un mínimo relativo en el punto $\left( {1,\,\,0} \right)$ con valor $f\left( {1,\,0} \right) = {1 \over {100}}{e^{ - 1}} + 30$.
Apartado b
Como la función $f$ es continua en la región $D$, que es acotada y contiene a su frontera, se tiene asegurado que $f$ alcanzará los valores máximo y mínimo absoluto en $D$ (ver teorema de Weierstrass).Al ser $f$ diferenciable, los puntos que serán extremos absolutos son
- puntos frontera de $D$ o
- puntos del interior de $D$ donde el gradiente de $f$ es nulo.
El punto interior ya está analizado en el apartado anterior por lo que faltaría estudiar ahora los puntos frontera. En cuanto realices el estudio, pulsa sobre el botón
Puntos sobre la circunferencia
En la frontera de $D$ los puntos son de la forma $\left( {x,y} \right)$ con ${x^2} + {y^2} = 4$.En esos puntos la función es: $$h\left( x \right) = {1 \over {100}}{e^{4 - 2x}} + 30\,\,\,\,\,\,\,\, x \in \left[ { - 2,\,\,2} \right]$$ cuya gráfica es
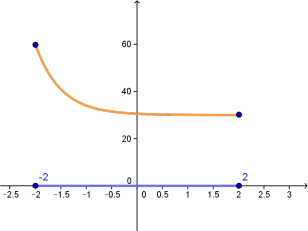
Los puntos extremos de $h$ se obtienen para $x = - 2$ y $x = 2$. En consecuencia $f$ tiene extremos en:
- el punto $\left( {2,0} \right)$ de valor $f\left( {2,0} \right) = 30.01$
- el punto $\left( {-2,0} \right)$ de valor $f\left( { - 2,0} \right) = {1 \over {100}}{e^8} + 30$
Una vez analizados todos los puntos críticos, calcula el valor máximo y mínimo absoluto de la función $f$ en $D$. En cuanto lo tengas pulsa sobre el botón
Análisis de los extremos absolutos
Conclusión:- El valor mínimo absoluto de la función $f$ en $D$ se alcanzan el el punto $\left( {1,\,0} \right)$ tomando el valor $f\left( {1,\,0} \right) = {1 \over {100}}{e^{ - 1}} + 30$.
- El valor máximo absoluto de la función $f$ en $D$ se alcanzan en el punto $\left( { - 2,\,0} \right)$ tomando $f$ el valor $f\left( { - 2,0} \right) = {1 \over {100}}{e^8} + 30$.