Enunciado
Dada la función $f\left( {x,y} \right) = 2x + 2y - {x^2} - {y^2} - 23$, se pide determinar los puntos máximos y mínimos absolutos sobre la placa triangular D del primer cuadrante acotada por las rectas $x = 0,\,\,y = 0,\,\,y = 9 - x$.
Representación de la función
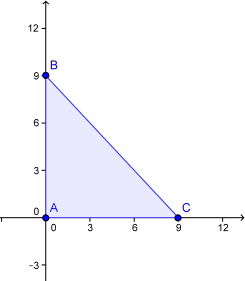
El dominio $D$, en el que tenemos que calcular los valores máximos y mínimos de la función $f$, es el conjunto del plano que se muestra en la figura siguiente:
Representamos también la gráfica de la función $f$, la frontera $C$ del dominio $D$ (curva en azul del plano $z=0$) y la curva imagen de $C$ por $f$ (curva en color naranja).
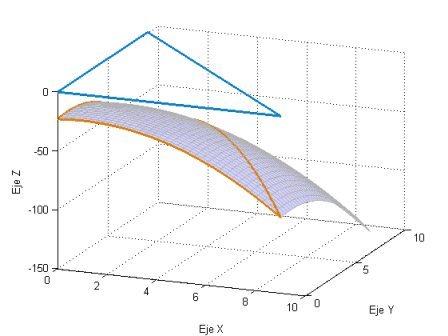

Representamos también la gráfica de la función $f$, la frontera $C$ del dominio $D$ (curva en azul del plano $z=0$) y la curva imagen de $C$ por $f$ (curva en color naranja).

Puntos críticos
Como la función $f$ es continua en la región $D$, que es acotada y contiene a su frontera, se tiene asegurado que $f$ alcanzará los valores máximo y mínimo absoluto en $D$ (ver teorema de Weierstrass).Al ser $f$ diferenciable los puntos que serán extremos absolutos serán
- puntos frontera del triángulo $D$ o
- puntos del interior de $D$ donde el gradiente de $f$ es nulo
Calcula los puntos críticos de $f$ en el interior de $D$ y, en cuanto lo tengas, pulsa sobre el botón
Puntos críticos en el interior de $D$
Serán los que cumplen $$f_x^' = 2 - 2x = 0\,\,\,\,\,\,\,\,\,\,\,\,f_y^' = 2 - 2y = 0$$ Resolviendo este sistema, el punto es: $\left( {1,\,\,1} \right)$ con valor $f\left( {1,\,\,1} \right) = - 21$.Analizamos ahora la frontera de $D$. Empieza calculando los puntos críticos de $f$ en el segmento que une los puntos $\left( {0,\,\,0} \right)$ con $\left( {9,\,\,0} \right)$. En cuanto lo tengas pulsa sobre el botón
Puntos del segmento que une $\left( {0,\,\,0} \right)$ con $\left( {9,\,\,0} \right)$
En este caso la función es: $$h\left( x \right) = f\left( {x,0} \right) = - 23 + 2x - {x^2}\,\,\,\,\,\,\,\,\,\,x \in \left[ {0,9} \right]$$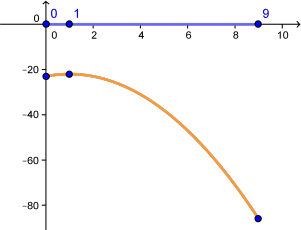
Esta es una función de una variable con puntos extremos $x=0$ , $x=9$ y $x=1$, cumpliendo $$f\left( {0,0} \right) = - 23 \,\,\,\,\,\,\,\,\,\,f\left( {9,0} \right) = - 86\,\,\,\,\,\,\,\,\,\,f\left( {1,0} \right) = - 22$$
Calcula los puntos críticos de $f$ en el segmento que une los puntos $\left( {0,\,\,0} \right)$ con $\left( {0,\,\,9} \right)$ y, en cuanto lo tengas, pulsa sobre el botón
Puntos del segmento que une $\left( {0,\,\,0} \right)$ con $\left( {0,\,\,9} \right)$
Para estos puntos la función se transforma en $$g\left( y \right) = f\left( {0,y} \right) = - 23 + 2y - {y^2}\,\,\,\,\,\,\,\,\,\,\,y \in \left[ {0,9} \right]$$
Esta es una función de una variable con puntos extremos $y=0$ , $y=9$ y $y=1$, cumpliendo $$f\left( {0,0} \right) = - 23 \,\,\,\,\,\,\,\,\,\,f\left( {0,9} \right) = - 86\,\,\,\,\,\,\,\,\,\,f\left( {0,1} \right) = - 22$$
Calcula los puntos críticos de $f$ en el segmento que une los puntos $\left( {0,\,\,9} \right)$ con $\left( {9,\,\,0} \right)$ y, en cuanto lo tengas, pulsa sobre el botón
Puntos del segmento que une $\left( {0,\,\,9} \right)$ con $\left( {9,\,\,0} \right)$
Para estos puntos la función se transforma en $$t\left( x \right) = f\left( {x,9 - x} \right) = - 23 + 2x + 2\left( {9 - x} \right) - {x^2} - {\left( {9 - x} \right)^2} = - 86 + 18x - 2{x^2}\,\,\,\,\,\,\,\,\,\,x \in \left[ {0,9} \right]$$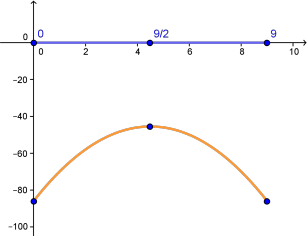
Esta es una función de una variable con puntos extremos: $x=0,\,\,x = {9 \over 2}, \,\,x=9$, cumpliendo $$f\left( {0,9} \right) = - 86 \,\,\,\,\,\,\,\,\,\,f\left( {{9 \over 2},{9 \over 2}} \right) = - {{91} \over 2}\,\,\,\,\,\,\,\,\,\,f\left( {9,0} \right) = - 86$$
Una vez analizados todos los puntos críticos de $D$, calcula el valor máximo y mínimo absoluto de la función $f$. En cuanto lo tengas pulsa sobre el botón
Análisis de los extremos absolutos
Conclusión:- El valor máximo absoluto de la función $f$ en $D$ se alcanza en el punto $\left( {1,1} \right)$ con valor $f\left( {1,1} \right) = -21$.
- Los valores mínimos absolutos de $f$ en $D$ se alcanzan en los puntos $\left( {0,9} \right)$ y $\left( {9,0} \right)$ con valor $f\left( {0,9} \right) = f\left( {9,0} \right) = -86$.