Los primeros términos de un desarrollo en serie

Índice de tema

Enunciado

Sea $f(x)=(\mbox{arctg}\, x)^2$ en $|x|<1$

Encuentra los cuatro primeros términos del desarrollo de $f(x)$ en serie de potencias de $x$, para $|x|<1$;
¿Cuánto vale $f^{(n}(0)$ si $n$ es impar?¿Cuánto vale $f^{(8}(0)$?
Comprueba en el ordenador los resultados de los apartados anteriores y dibuja las gráficas de la suma de los cuatro primeros términos del desarrollo junto con la de la función en el intervalo $(-.99,.99)$.

Resolución primer apartado

Una buena manera de encontrar los primeros términos de desarrollo pedido es

Hacer el polinomio de Taylor del grado que haga falta.

Elevar al cuadrado la serie correspondiente a $g(x)=\mbox{arctg}\, x$

Lo malo es encontrar las derivadas necesarias; no es imposible, pero puede resultar bastante trabajoso.

Puesto que sólo pide unos pocos sumandos y no el término general, éste método sí es de fácil aplicación aquí.

Paso 1

Por tanto, como primer paso encontremos el desarrollo de $g(x)=\mbox{arctg}\, x$. Para ello derivaremos $g(x)$ y utilizaremos la suma de la serie geométrica . Inténtalo y pulsa en 'Continuar'.

$$g'(x)=\frac{1}{1+x^2}=\sum_{n=0}^\infty (-1)^nx^{2n}$$ Este desarrollo es válido en $|x|<1$; así $$g(x)=\int_0^x g'(t)\, dt = \sum_{n=0}^\infty (-1)^n \int_0^x t^{2n}= \sum_{n=0}^\infty \frac{(-1)^n}{2n+1} x^{2n+1}$$

Paso 2

Ahora debemos multiplicar ese desarrollo por sí mismo para obtener, únicamente, los primeros cuatro términos: $$f(x)=(\mbox{arctg}\, x)^2=\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots\right)^2$$ La suma de los primeros cuatro términos de esta serie es

$$x^2+\left(\frac{x^3}{3}\right)^2+\left(\frac{x^5}{5}\right)^2+\left(\frac{x^7}{7}\right)^2$$

$$x^2+\left(-\frac{1}{3}-\frac{1}{3}\right)x^4+\left(\frac{1}{5}+\frac{1}{9}+\frac{1}{5}\right)x^6+ +\left(-\frac{1}{7}-\frac{1}{15}-\frac{1}{15}-\frac{1}{7}\right)x^8$$

Tremendo error. La suma, sea finita o infinita, al cuadrado no es la suma de los cuadrados.

En efecto. Podemos escribir $$f(x)\approx x^2-\frac{2}{3}x^4+\frac{23}{45}x^6-\frac{44}{105}x^8$$

Resolución segundo apartado

Para contestar a las cuestiones de este apartado, hemos de tener en cuenta que el desarrollo de una función en serie de potencias es único, sea cual sea el método por el que se obtuvo: $$f(x)=\sum_{n=0}^\infty \frac{f^{(n}(0)}{n!}x^n$$ Aunque en el apartado anterior no se haya obtenido el término general del desarrollo de $f(x)$ en serie de potencias de $x$, sí sabemos que $$f(x)=(\mbox{arctg}\, x)^2=\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots\right) \left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\ldots\right)$$ lo que significa que

el desarrollo de esta función tendrá únicamente sumandos de grado par, por tanto

Todas las derivadas de $f(x)$ de orden impar son nulas

No sabemos nada de las derivadas de $f(x)$ de orden impar

Todas las derivadas de $f(x)$ de orden impar son nulas en $x=0$

No es correcto, piénsalo bien.

Sí deberíamos saber algo. Piénsalo bien.

En efecto, eso es lo correcto. Para cualquier $n$ impar, $f^{(n}(0)=0$.

¿Cuánto vale $f^{(8}(0)$? El coeficiente de $x^8$ en $$f(x)=\sum_{n=0}^\infty \frac{f^{(n}(0)}{n!}x^n$$ es $$\frac{f^{(8}(0)}{8!}$$ y en el primer apartado obtuvimos para ese coeficiente el valor $-\frac{44}{105}$, luego $$f^{(8}(0)=-\frac{44}{105}8!=-16896$$

Resolución tercer apartado

La suma de los cuatro primeros términos del desarrollo $$x^2-\frac{2}{3}x^4+\frac{23}{45}x^6-\frac{44}{105}x^8$$ es el polinomio de Taylor de $f(x)$ de orden 8 centrado en $a=0$. Por tanto, en el ordenador se obtendrá con
```
syms x % se declara x como simbólica
t8=taylor(atan(x)^2,9,0) % se calcula el polinomio de Taylor de grado 8 y centro 0
```

Para comprobar el valor de la derivada de orden 8 en $x=0$, podemos ejecutar

d8=diff(atan(x)^2,8) % se supone que x ya ha sido declarada simbólica
subs(d8,0)

Para dibujar el polinomio y la función, podemos continuar en simbólico y utilizar el comando 'ezplot'. Suponiendo que ya está calculado 't8', escribiremos
```
ezplot(t8,[-.99,.99])
hold on
ezplot(atan(x)^2,[-.99,.99])
hold off
```
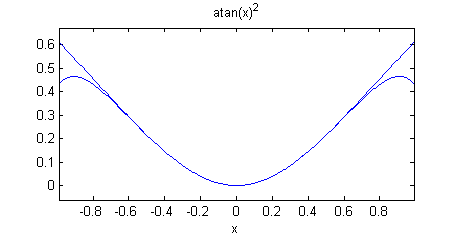
Puesto que las dos gráficas las dibuja en azul, pidiendo
```
subs(t8,1)
atan(1)^2
```
sabemos que la gráfica superior es la de $f(x)$ y la inferior la de su polinomio de Taylor de grado 8 y centro 0; de hecho, el polinomio tiende a $-\infty$ cuando $x$ tiende a $\infty$, mientras que la función tiende a $\pi^2/4$.

Índice de tema