Enunciado
Encuentra el polinomio de Taylor de grado 2 y centro $a=0$ de la función $$f(x)=\frac{x^3}{6}+e^x(8x-x^2-19)$$ y halla una cota del error cometido cuando se utiliza este polinomio para aproximar $f(1.5)$.
Hacemos en el ordenador el polinomio pedido, con
syms x f=x^3/6+exp(x)*(8*x-x^2-19); t2=taylor(f,3,0)se obtiene que $$T_2(x)=-19-11x-\frac{5}{2}x^2$$ Sabemos que el resto es $$R_2(x)=\frac{f'''(t)}{6}x^3$$ con $t$ entre 0 y $x$. Para $x=1.5$, $$R_2(1.5)=\frac{f'''(t)}{6}1.5^3$$ con $t$ entre 0 y $1.5$. Acotamos $f'''(t)$ para $t\in[0,1.5]$. Para ello hemos de calcular $f'''(t)$; lo podemos hacer en el ordenador con
f3=diff(f,3) % se supone que f está ya definidaresulta $$f'''(x)=1-(x-1)^2e^x$$ puesto que $f'''(0)=0$ y $f'''(1.5)=-0.1204$, acotamos el resto de la siguiente manera $$|R_2(1.5)|< \frac{0.1204}{6}1.5^3=0.0677$$ Según esto, la diferencia entre $T_2(1.5)$ y $f(1.5)$ debería ser menor que $0.0677$. Sin embargo, $$T_2(1.5)=-41.125$$ y $$f(1.5)=-40.8931$$ es decir una diferencia de $0.2319$, que desde luego es mayor que $0.0677$. ¿Dónde está el error? Piénsalo y pulsa en 'Continuar'.
Puedes dibujar la gráfica de $f'''(x)$ en $[0,1.5]$ poniendo
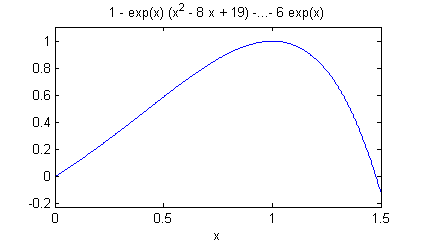
Claramente, la cota escogida para $f'''(t)$ con $t\in[0,1.5]$ fue errónea. El valor absoluto de esta función no está acotado por el valor absoluto de la función en el extremo derecho, ni tampoco por su valor en el extremo izquierdo. Una cota correcta será $f'''(1)=1$, con lo cual, acotaremos el error por $$|R_2(1.5)|< \frac{1}{6}1.5^3=0.5625$$ que como observamos sí es mayor que el error real, $0.2319$.
ezplot(f3,[0,1.5])

Claramente, la cota escogida para $f'''(t)$ con $t\in[0,1.5]$ fue errónea. El valor absoluto de esta función no está acotado por el valor absoluto de la función en el extremo derecho, ni tampoco por su valor en el extremo izquierdo. Una cota correcta será $f'''(1)=1$, con lo cual, acotaremos el error por $$|R_2(1.5)|< \frac{1}{6}1.5^3=0.5625$$ que como observamos sí es mayor que el error real, $0.2319$.