Comenzamos encontrando el desarrollo de MacLaurin de $f(x)$. No es neceario recurrir a la derivada $n$-ésima, ya que $f'(x)$ es la suma de una serie geométrica: $$f'(x)=\frac{1}{1+x^2} \ \ \ \Rightarrow \ \ \ f'(x)=\sum_{n=0}^\infty (-1)^nx^{2n} \ \ \ \Rightarrow \ \ \ f(x)=\sum_{n=0}^\infty (-1)^n \frac{x^{2n+1}}{2n+1}$$ Si ahora tomamos ese desarrollo en $x=\sqrt{3}$, $$S=\sum_{n=0}^\infty (-1)^n \frac{\sqrt{3}^{2n+1}}{2n+1}=\sqrt{3}\sum_{n=0}^\infty \frac{(-3)^n}{2n+1}$$ resulta esa serie, de la que tomamos los primeros cinco términos: $$S\approx S_5= \sqrt{3}\sum_{n=0}^4 \frac{(-3)^n}{2n+1}$$ Con el ordenador calculamos rápidamente $S_5$, poniendo

	n=0:4;
	sum((-1).^n.*sqrt(3).^(2*n+1)./(2*n+1))

resulta $S_5=12.0254$. Sin embargo, esa no es una buena aproximación de $f(\sqrt{3})=\mbox{arctg}\,\sqrt{3}$, pues sabemos que $$\mbox{arctg}\,\sqrt{3}=\frac{\pi}{3}\approx 1.0472$$ ¿Dónde está el error? Piénsalo y pulsa en 'Continuar'. Continuar

Es claro que $x=\sqrt{3}$ no está en el campo de convergencia de $$f(x)=\sum_{n=0}^\infty (-1)^n \frac{x^{2n+1}}{2n+1}$$ ya que se ha obtenido integrando la serie geométrica $$f'(x)=\sum_{n=0}^\infty (-1)^nx^{2n}$$ cuyo radio de convergencia es $1$; aunque no hayamos averiguado si la serie correspondiente a $f(x)$ es convergente en los extremos del intervalo de convergencia, desde luego sabemos que $x=\sqrt{3}$ se sale del campo. En la figura podemos observar que a la derecha de $x=1$ las primeras cinco sumas parciales se van alejando de la función $f(x)$ (gráfica amarilla). En particular, vemos cómo se alejan en $x=3$ (eje vertical azul):

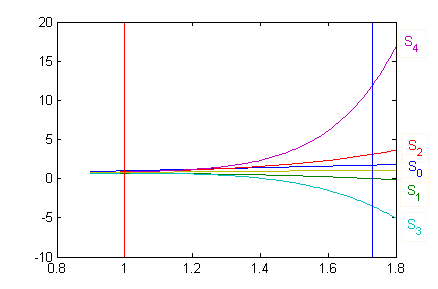
f=@(x,n) (-1)^n*x.^(2*n+1)/(2*n+1);
x=0.9:.01:1.8;
s(1,:)=f(x,0);
for k=2:5
	s(k,:)=s(k-1,:)+f(x,k-1);
end
s(6,:)=atan(x);
plot(x,s)
hold on
plot([1 1],[-10 20],'r')
plot([sqrt(3) sqrt(3)],[-10 20])
hold off
clear all

Para buscar un polinomio que nos sirviera para aproximar $f(\sqrt{3})$ deberíamos centrarlo más cerca de $x=\sqrt{3}$.