Llamamos $$a_n=\frac{2^n}{n}$$ y hacemos el límite $$\lim_{n\rightarrow \infty} \left|\frac{a_{n+1}}{a_n}\right|=\lim_{n\rightarrow \infty}\frac{2^{n+1}}{n+1} \frac{n}{2^n}=\lim_{n\rightarrow \infty}\frac{2n}{n+1}=2$$ Según esto, el radio sería $\frac{1}{2}$.

Sin embargo, si tomamos $x=0.6=\frac{3}{5}$ y evaluamos la serie en él, resulta $$\sum_{n=0}^\infty \frac{2^n3^{2n+1}}{n 5^{2n+1}}$$ que podemos comprobar que es una serie numérica convergente: $$\lim_{n\rightarrow \infty} \left|\frac{a_{n+1}}{a_n}\right|= \lim_{n\rightarrow \infty} \frac{2^{n+1}3^{2n+3}}{(n+1) 5^{2n+3}}\frac{n 5^{2n+1}}{2^n3^{2n+1}}=$$ $$=\lim_{n\rightarrow \infty} \frac{18 n}{25(n+1)}=\frac{18}{25}< 1$$ Según esto, la serie de potencias es convergente en $x=0.6$ siendo $|x|>0.5$. ¿Dónde está el error? Piénsalo y pulsa en 'Continuar'. Continuar

El radio está mal calculado. No podemos quedarnos únicamente con la expresión de $a_n$ sin tener en cuenta a qué potencias de $x$ acompaña. La fórmula $$R=\frac{1}{L}\ \ \mbox{con}\ \ L=\lim_{n\rightarrow \infty} \left|\frac{a_{n+1}}{a_n}\right|$$ no sirve si las potencias no son consecutivas y $L$ no es $1$. Por eso, lo más seguro es aplicar el criterio del cociente al valor absoluto de todo el término general, no sólo a los coeficientes: $$\lim_{n\rightarrow \infty} \left|\frac{a_{n+1}x^{2n+3}}{a_nx^{2n+1}}\right|= \lim_{n\rightarrow \infty} \frac{2n}{n+1} |x|^2=2|x|^2< 1\ \ \Rightarrow \ \ |x|< \frac{1}{\sqrt{2}}$$ Así nos ha salido directamente el radio de convergencia correcto: $$R=\frac{1}{\sqrt{2}}$$ En la figura puedes ver las primeras sumas parciales de esta serie

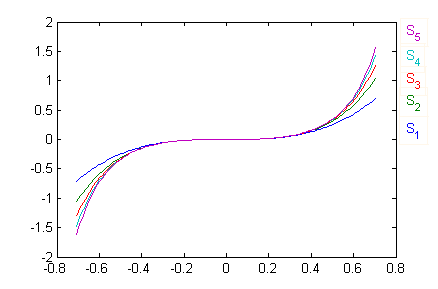
f=@(x,n) 2^n*x.^(2*n+1)/n;
r=1/sqrt(2);
x=-r:.01:r;
s(1,:)=f(x,1);
for k=2:5
	s(k,:)=s(k-1,:)+f(x,k);
end
plot(x,s)
clear all