Ejercicios preliminares e instantáneos. Sumatorios finitos e infinitos

1. $\sum_{n=0}^6 (n-3)$ tiene 6 sumandos no nulos pues $n-3$ se anula en $n=3$
2. $\sum_{n=0}^5 (2n-3)$ tiene 6 sumandos (todos) no nulos, pues $2n-3$ no se anula en ninguno de los valores que toma $n$
3. $\sum_{n=-2}^{10} (3-n^2)$ tiene 13 sumandos no nulos (todos), pues $3-n^2$ no se anula en ninguno de los valores que toma $n$.

Si queremos generar (pero no sumar) estos números en el ordenador podemos escribir

1. 		(0:6)-3
   		

2. 		2*(0:5)-3 

3. 		3-(-2:10).^2
   	

De otra forma, menos compacta pero quizá mas fácil de visualizar, definiremos $n$ como un vector que contiene a todos los índices que debe recorrer el sumatorio:

1. 	n=0:6; % vector de índices
   	n-3 % operación con esos índices
   	

2. 	n=0:5; % vector de índices
   	2*n-3 % operación con esos índices 

3. 	n=-2:10; % vector de índices
   	3-n.^2 % operación con esos índices
   	

Todos los sumatorios son la misma suma: $$1+2^2+3^2+4^2+5^2+6^2$$ Para efectuarla en el ordenador pondremos

  		n=1:6;  % vector de índices
  		sum(n.^2)  % suma 1+2^2+3^2+4^2+5^2+6^2
  		

Por ejemplo, el sumatorio equivalente a $\sum_{n=1}^{4} n^3$ empezando en $n=0$ es $\sum_{n=0}^{3} (n+1)^3$
Ver solución

1. $\sum_{n=1}^{6} \frac{1}{n+1}=\sum_{n=0}^{5} \frac{1}{n+2}$
2. $\sum_{n=2}^{5} \sqrt{(n+1)^2-2}=\sum_{n=0}^{3} \sqrt{(n+3)^2-2}$
3. $\sum_{n=-1}^{10} x^n=\sum_{n=0}^{11} x^{n-1}$
4. $\sum_{n=1}^6 \frac{(-1)^{n-1}}{2n-1}=\sum_{n=0}^5 \frac{(-1)^{n}}{2n+1}$
5. $\sum_{n=-3}^{8} x^{2n}=\sum_{n=0}^{11} x^{2(n-3)}$

1. $\sum_{n=2}^{10} n^3$ suma los cubos de todos los naturales entre 2 y 10, luego no es $2^3+4^3+6^3+8^3+10^3$
2. $\sum_{n=1}^{10} (n+1)^3$ suma los cubos de todos los naturales entre 2 y 11, luego no es $2^3+4^3+6^3+8^3+10^3$
3. $\sum_{n=0}^5 (2n)^3=0+2^3+4^3+6^3+8^3+10^3$, sí es correcto
4. $\sum_{n=0}^4 [2(n+1)]^3=2^3+4^3+6^3+8^3+10^3$, sí es correcto

Para hacer la suma $2^3+4^3+6^3+8^3+10^3$ en el ordenador podemos optar por

		n=1:5; % vector de índices
		sum((2*n).^3)  % suma 2^3+4^3+6^3+8^3+10^3
		

o por

				n=2:2:10; % vector de pares entre 2 y 10
				sum(n.^3)  % suma 2^3+4^3+6^3+8^3+10^3
		

1. $\sum_{n=1}^{13} \frac{1}{n}$ incluye pares e impares, mientras la suma $1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}+\frac{1}{13}$ es sólo de los inversos de los impares
2. $\sum_{n=0}^{12} \frac{1}{n+1}$ es la misma suma que la del apartado anterior
3. $\sum_{n=0}^6 \frac{1}{2n+1}$ sí es correcta, pues $2n+1$ para $n=0$ hasta $n=6$ recorre los impares desde 1 hasta 13
4. $\sum_{n=1}^7 \frac{1}{2n-1}$ sí es correcta, es la misma suma del apartado anterior.

Para hacer la suma $1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}+\frac{1}{13}$ en el ordenador podemos optar por

		n=1:7; % vector de índices
		sum(1./(2*n-1))  % suma  1+1/3+1/5+1/7+1/9+1/11+1/13
		

o por

				n=1:2:13; % vector de impares del 1 al 13
				sum(1./n)  % suma 1+1/3+1/5+1/7+1/9+1/11+1/13
		

1. $2\sum_{n=0}^\infty n^2$ es igual a $\sum_{n=0}^\infty 2n^2$, pues en una suma finita o infinita podemos sacar factor común.
2. $\sum_{n=0}^\infty (2^n n^2)$ es distinto a $2^n\sum_{n=0}^\infty n^2$, pues el factor $2^n$, al depender de $n$, no es común a todos los términos. De hecho la expresión $2^n\sum_{n=0}^\infty n^2$ es poco afortunada, pues si $n$ es una constante o variable conocida, no debería utilizarse ese mismo nombre para el índice del sumatorio.

1. $\sum_{n=1}^5 \frac{(-1)^n}{n}$ tiene 3 sumandos negativos, pues $(-1)^n=-1$ para $n=1$, $n=3$ y $n=5$
2. $\sum_{n=0}^6 \frac{(-1)^{2n}}{n+2}$ no tiene ningún sumando negativo, pues $(-1)^{2n}$ es siempre positivo
3. $\sum_{n=0}^6 \frac{(-1)^{2n-1}}{n+2}$ tiene sus 7 sumandos negativos, pues $(-1)^{2n-1}=(-1)^{-1}=-1$ para cualquier $n$
4. $\sum_{n=2}^7 \frac{(-1)^{n+1}}{n^3}$ tiene 3 sumandos negativos, pues $(-1)^{n+1}=-1$ para $n=2$, $n=4$ y $n=6$
5. $\sum_{n=2}^7 \frac{(-1)^{n-1}}{n^3}$ tiene 3 sumandos negativos, pues $(-1)^{n-1}=-1$ para $n=2$, $n=4$ y $n=6$
6. $\sum_{n=1}^4 \frac{\cos n\pi}{n}$ tiene 2 sumandos negativos, pues $\cos n\pi=(-1)^n=-1$ para $n=1$ y $n=3$

En el ordenador podemos generar los términos de estas expresiones (sin sumarlos) con

1. 				n=1:5; % vector de índices
   				(-1).^n./n  % términos del sumatorio
   		

2. 				n=0:6; % vector de índices
   				(-1).^(2*n)./(n+2)  % términos del sumatorio
   		

3. 				n=0:6; % vector de índices
   				(-1).^(2*n-1)./(n+2)  % términos del sumatorio
   		

4. 				n=2:7; % vector de índices
   				(-1).^(n+1)./n.^3  % términos del sumatorio
   		

5. 				n=2:7; % vector de índices
   				(-1).^(n-1)./n.^3  % términos del sumatorio
   		

6. 				n=1:4; % vector de índices
   				cos(n*pi)./n  % términos del sumatorio
   		

1. $1-a+a^2-a^3+a^4=\sum_{n=0}^4 (-1)^n a^n$
2. $b+\frac{b^2}{2!}+\frac{b^3}{3!}+\frac{b^4}{4!}+\frac{b^5}{5!}=\sum_{n=1}^5 \frac{b^n}{n!}$
3. $1-\frac{c^2}{2}+\frac{c^4}{4!}-\frac{c^6}{6!}=\sum_{n=0}^3 (-1)^n\frac{c^{2n}}{(2n)!}$
4. $d-\frac{d^3}{3!}+\frac{d^5}{5!}-\frac{d^7}{7!}=\sum_{n=0}^3 (-1)^n\frac{d^{2n+1}}{(2n+1)!}$

Por ejemplo, $$\sum_{n=1}^\infty \frac{x^n}{(n-1)!}=x+x^2+\frac{x^3}{2}+\sum_{n=4}^\infty \frac{x^n}{(n-1)!}$$ Ver solución

1. $\sum_{n=0}^\infty \frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\sum_{n=4}^\infty \frac{x^n}{n!}$
2. $\sum_{n=0}^\infty \frac{x^{2n}}{n!}=1+\frac{x^2}{2}+\sum_{n=2}^\infty \frac{x^{2n}}{n!}$
3. $\sum_{n=0}^\infty \frac{(-1)^nx^{2n}}{n!}=1-x^2+\sum_{n=2}^\infty \frac{(-1)^nx^{2n}}{n!}$
4. $\sum_{n=0}^\infty \frac{x^{4n}}{(n+1)!}=1+\sum_{n=1}^\infty \frac{x^{4n}}{(n+1)!}$

1. $$\sum_{n=0}^6 \frac{1}{n+1}+ \sum_{n=0}^6 \frac{2}{n+3}=\sum_{n=0}^6 \frac{3n+5}{(n+1)(n+3)}$$ Puedes comprobarlo con

   		n=0:6; % vector de índices
   		sum(1./(n+1))+sum(2./(n+3)) % dos sumatorios
   		sum((3*n+5)./((n+1).*(n+3))) % un único sumatorio
   		

2. $$\sum_{n=1}^4 (2n)^2+ \sum_{n=1}^3 (2n+1)^2=\sum_{n=2}^8 n^2$$ En este caso,

   				n=1:4;k=2:8; % vectores de índices
   				sum((2*n).^2)+sum((2*n(1:3)+1).^2) % dos sumatorios
   				sum(k.^2) % un único sumatorio
   		

3. $$\sum_{n=1}^4 (2n)^2- \sum_{n=2}^4 (2n-1)^2=\sum_{n=2}^8 (-1)^n n^2$$ Podemos escribir:

   		sum((2*(1:4)).^2)-sum((2*(2:4)-1).^2) % dos sumatorios
   		sum((-1).^(2:8).*(2:8).^2) % un único sumatorio
   		

$S(-1)=0$; $S(0)=1$; $S(1)=6$.
En el ordenador podemos generar esta función y evaluarla de la siguiente manera:

		s = @(a) sum(a.^(0:5));
		s(-1)
		s(0)
		s(1)
		

$S(-2)=\frac{-76}{15}$; $S(0)=0$; $S(2)=\frac{256}{15}$.

		n=1:5;
		s = @(a) sum(a.^n./n);
		s(-2)
		s(0)
		s(2)
		

1. $2^{-3},\, 2^{-2},\, 2^{-1},\, 1$ están en progresión geométrica de razón 2
2. $-4,\, -\frac{4}{3},\, -\frac{4}{9},\, -\frac{4}{27}$ están en progresión geométrica de razón $1/3$
3. $3,\, -3,\, 3,\, -3$ están en progresión geométrica de razón $-1$
4. $-3,\, 3\sqrt{2},\, -6,\, 6\sqrt{2}$ están en progresión geométrica de razón $-\sqrt{2}$

Recuerda que la suma de los $n$ primeros términos de una progresión geométrica viene dada por $$a_1+a_1r+a_1r^2+\ldots + a_1r^{n-1}=a_1\frac{1-r^n}{1-r}$$ Esta fórmula se obtiene fácilmente restando de $$S_n=a_1+a_1r+a_1r^2+\ldots + a_1r^{n-1}$$ la expresión $$rS_n=a_1r+a_1r^2+a_1r^3+\ldots + a_1r^{n-1}+a_1r^n$$ y despejando $S_n$.
Ver solución

1. $2^{-3}+2^{-2}+2^{-1}+1=2^{-3}\frac{1-2^{-4}}{1-2}=\frac{15}{8}$; puedes comprobar este resultado con

   		 sum(2.^(-3:0))
   		

2. $-4-\frac{4}{3} -\frac{4}{9} -\frac{4}{27}=-4\frac{1-81^{-1}}{1-3^{-1}}=-\frac{480}{81}$

   				 sum(-4./(3.^(0:3)))
   		

3. $3 -3+ 3-3=0$ (aquí no hace falta aplicar la fórmula)
4. $-3+3\sqrt{2}-6+6\sqrt{2}=-3\frac{1-(-\sqrt{2})^{4}}{1+\sqrt{2}}=\frac{9}{1+\sqrt{2}}$

   		 sum(-3*(-sqrt(2)).^(0:3))
   		

El enunciado es verdadero, pues los números que se suman son de la forma $\frac{(a^2)^n}{n}$. En la figura puedes ver ese sumatorio evaluado en un conjunto de puntos entre $-1$ y $1$:

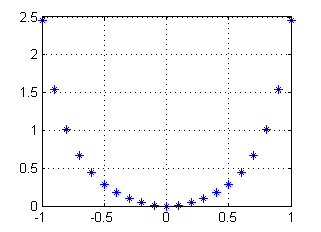
Puedes hacerla con

		n=1:6;  			% vector de índices
		syms a; 			% se define a como variable simbólica
		s=sum(a.^(2*n)./n) 	% definición del sumatorio
		x=-1:.1:1;			% valores donde se evaluará el sumatorio
		y=subs(s,a,x)  		% evaluación del sumatorio en los puntos
		plot(x,y,'*') 		% dibujo de los valores y sobre los x
		grid on
		

Si no recurrimos al paquete simbólico, podemos hacer un ciclo para ir acumulando los sumandos:

		a=-1:.1:1; 				% puntos donde evaluaremos el sumatorio
		s=zeros(size(a)); 		% se inicializa s como cero
		for n=1:6				% comienza el ciclo sobre los índices del sumatorio
			s=s+a.^(2*n)./n		% se acumulan en s los sumandos
		end
		plot(a,s,'*')			% dibujo de los valores de s sobre los de a
		grid on

El enunciado es falso, pues para cada $n$, el número $\frac{a^{2n}}{n!}$ es menor que el número $\frac{a^{2n}}{n}$, luego la suma $\sum_{n=1}^6 \frac{a^{2n}}{n!}$ es menor que la suma $\sum_{n=1}^6 \frac{a^{2n}}{n}$

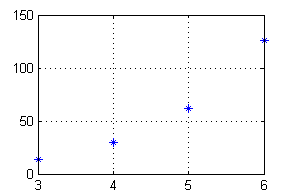
$S_3=14$, $S_4=30$, $S_5=62$ y $S_6=126$;
$S_4-S_3<S_5-S_4 < S_6-S_5$
La suma de todos los números de esa forma no puede ser finita, pues cada vez acumulamos números mayores:

		s(1)=6;
		for n=2:5
		s(n)=s(n-1)+2^(n+1)
		end
		plot(3:6,s(2:5),'*')
		grid on