Funciones periódicas y armónicos

Definición (Función periódica).- Una función $f(x)$ definida en un conjunto no acotado $D$, se llama periódica de periodo $T$ (o $T$-periódica) si existe un número $T>0$ tal que para cada $x\in D$ se cumple que $f(x+T)=f(x)$.

Nótese que si $T$ es periodo de $f(x)$ también los números $2T$, $3T$, etc. son periodos de $f(x)$: $$f(x)=f(x+T)=f(x+2T)=\ldots=f(x+nT)$$ para cualquier $n$ natural.

Si $T$ es el menor número positivo que verifica esta condición, le llamaremos periodo propio o fundamental. Cuando no indiquemos lo contario supondremos que nos referimos al periodo fundamental.

Definición (Función armónica o armónico).- Se llama función armónica o simplemente armónico a una función periódica definida por una de las ecuaciones siguientes $$f(x)=A\cos(\omega x+\phi)\ \ \mbox{o}\ \ f(x)=A\,\mbox{sen}(\omega x+\phi)$$

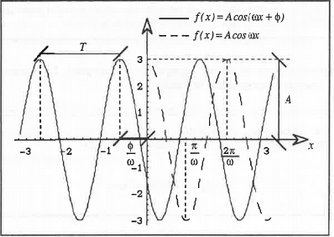
Como se desprende de la definición, los armónicos son ondas senoidales o cosenoidales cuya forma viene determinada por los valores siguientes:

• $A$, es la amplitud o altura de la sinusoide,

• $\phi$, es el ángulo de fase e indica al punto de arranque dentro del ciclo,

• $\omega$, es la frecuencia angular medida en rad/s

La frecuencia angular $\omega$ es el parámetro determinante de la forma de la senoide y va a jugar un papel fundamental en todo el análisis de Fourier. Si llamamos $f$ a la frecuencia en ciclos/s, se tiene que $$\omega=2\pi f$$ y puesto que $T$ es la duración de un ciclo u oscilación, $f=\frac{1}{T}$, con lo cual $$\omega=\frac{2\pi}{T}=\frac{\pi}{p}$$ siendo $p$ el semiperiodo.

Nótese que $\frac{\phi}{\omega}$ es la traslación que debe aplicarse al armónico $f(x)=A\cos(\omega x+\phi)$ para que su gráfica coincida con la de otro armónico de la misma frecuencia pero que alcanza el máximo para $x=0$.

Series trigonométricas

Definición (Series trigonométricas o de Fourier).- Una serie de funciones del tipo $$\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos nx+b_n\,\mbox{sen} nx)$$ se llama serie trigonométrica y las constantes $a_0$, $a_n$, $b_n$, para cada $n$ natural, se llaman coeficientes de la serie trigonométrica.

Las funciones de la serie anterior son armónicos con ángulo de fase cero y periodo propio $T=2\pi/n$, por tanto, todas ellas tienen como periodo común $2\pi$.

Las sumas parciales $S_n(x)$ de esta serie son combinación lineal de funciones del sistema $$\{1,\, \cos x,\, \mbox{sen}\, x, \, \cos 2x,\, \mbox{sen}\, 2x,\, \ldots\}$$ que se llama sistema trigonométrico. Como los términos de esta serie son funciones periódicas con periodo $2\pi$, entonces en caso de que la serie anterior converja, su suma $S(x)$ será una función con periodo $2\pi$.

Definición (Desarrollo de una función en serie trigonométrica).- Desarrollar una función $f(x)$ con periodo $T=2\pi$ en serie trigonométrica significa hallar una serie de este tipo que sea convergente y cuya suma $S(x)$ sea igual a la función $f(x)$.

Veamos seguidamente que el sistema trigonométrico es ortogonal, recordando previamente ese concepto:

Definición (Funciones ortogonales).- Las funciones $f(x)$ y $g(x)$ continuas en el intervalo $[a,b]$ son ortogonales en $[a,b]$ si se cumple la condición $$\int_a^b f(x)\, g(x)\, dx=0$$

Definición (Sistema ortogonal de funciones).- Un sistema o familia de funciones $\varphi_1(x)$, $\varphi_2(x)$, $\ldots$, $\varphi_n(x)$, $\ldots$, continuas en el intervalo $[a,b]$, con $\varphi_i(x)\not\equiv 0$ para todo $i$ natural, se dice ortogonal en $[a,b]$ si para cualesquiera $n\neq m$ se cumple la condición $$\int_a^b \varphi_m(x)\, \varphi_n(x)\, dx=0$$

TEOREMA.- El sistema trigonométrico $$\{1,\, \cos x,\, \mbox{sen}\, x, \, \cos 2x,\, \mbox{sen}\, 2x,\, \ldots\}$$ es ortogonal en el intervalo $[-\pi,\pi]$.