Definición y obtención

Serie de Fourier en forma armónica.- La forma armónica para una función $f(x)$ $2p$-periódica es $$f(x)=A_0+\sum_{n=1}^\infty A_n\,\mbox{sen}\, (nwx+\phi_n)$$ o bien $$f(x)=A_0+\sum_{n=1}^\infty A_n\,\mbox{cos}\, (nwx-\varphi_n)$$ donde $w=\frac{\pi}{p}$ y $$A_0=\frac{a_0}{2}\ \ ,\ \ A_n=\sqrt{a^2_n+b^2_n}\ \ ,\ \ \phi_n=\mbox{arctg}\frac{a_n}{b_n}\ \ ,\ \ \varphi_n=\frac{\pi}{2}-\phi_n=\mbox{arctg}\frac{b_n}{a_n}$$ siendo $a_n$ y $b_n$ los coeficientes de la forma compleja.

Obtenemos estas expresiones a partir de la forma trigonométrica de la serie:

Partiendo de la forma trigonométrica de la serie de Fourier de una función $2p$-periódica, $$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nwx+b_n\,\,\mbox{sen}\, nwx)$$ donde $w=\frac{\pi}{p}$ y $$a_n=\frac{1}{p}\int_{-p}^p f(x)\cos nwx\,dx\ \ ,\ \ n=0,\, 1, \, \ldots$$ $$b_n=\frac{1}{p}\int_{-p}^p f(x)\,\mbox{sen}\, nwx\,dx\ \ ,\ \ n=1,\, 2, \, \ldots$$ aplicamos a cada par de términos de la misma frecuencia el procedimiento habitual para reducir la suma de un seno y un coseno del mismo ángulo a un sólo término, que en este caso es multiplicar y dividir por $\sqrt{a^2_n+b^2_n}$: $$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty \sqrt{a^2_n+b^2_n}\left(\frac{a_n}{\sqrt{a^2_n+b^2_n}}\cos nwx+\frac{b_n}{\sqrt{a^2_n+b^2_n}}\,\mbox{sen}\, nwx\right)$$ Considerando ahora el triángulo de la figura con las correspondientes relaciones trigonométricas

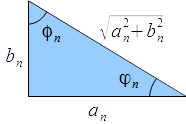
Si llamamos $A_n=\sqrt{a^2_n+b^2_n}$, $$a_n=A_n\,\mbox{sen}\,\phi_n\ ,\ \ b_n=A_n\cos\phi_n\ \ \ \Rightarrow\ \ \phi_n=\mbox{arctg}\frac{a_n}{b_n}$$ y sustituyendo en la expresión anterior resulta $$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty A_n\left(\mbox{sen}\,\phi_n\cos nwx+\cos\phi_n\mbox{sen}\, nwx\right)=A_0+\sum_{n=1}^\infty A_n\,\mbox{sen}\, (nwx+\phi_n)$$ Para obtener la forma armónica utilizando cosenos, trabajaremos con el ángulo $\varphi$, escribiendo $$a_n=A_n\cos\varphi_n\ ,\ \ b_n=A_n\,\mbox{sen}\,\varphi_n\ \ \ \Rightarrow\ \ \varphi_n=\mbox{arctg}\frac{b_n}{a_n}$$ y en el sumatorio, $$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty A_n\left(\cos\phi_n\cos nwx+\mbox{sen}\,\varphi_n\mbox{sen}\, nwx\right)=A_0+\sum_{n=1}^\infty A_n\cos (nwx-\varphi_n)$$

Espectro de frecuencias

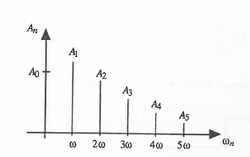
Definición (Espectro de frecuencias).- Dada una función $f(x)$, se llama así a la gráfica resultante de representar las amplitudes $A_n$ frente a las frecuencias $w_n$ múltiplos naturales de la frecuencia fundamental $w=\frac{\pi}{p}$.

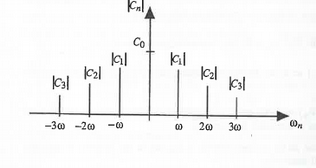
Es también habitual definir el espectro de frecuencias mediante los coeficientes complejos de la serie de Fourier. En este caso el espectro es la representación de $|c_n|$ frente a $w_n$ siendo $n$ entero. La relación entre $|c_n|$ y $A_n$ es $$|c_n|=\left|\frac{a_n-ib_n}{2}\right|=\frac{1}{2}\sqrt{a^2_n+b^2_n}=\frac{1}{2}A_n$$