Otras aplicaciones
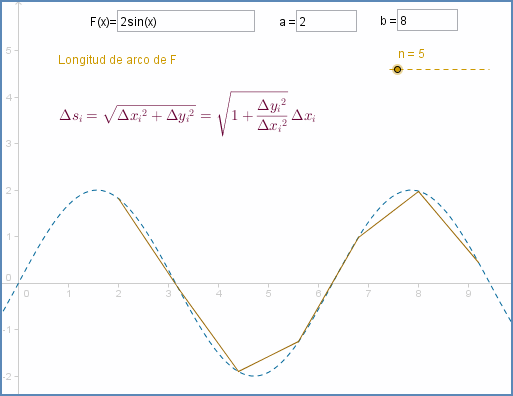
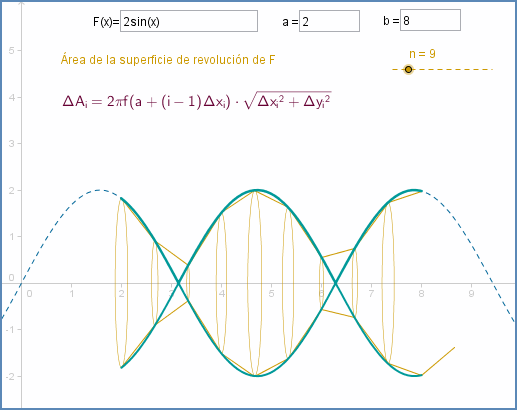
Cálculo de longitudes de curva
Diremos que la curva definida por la función $f$ es
rectificable en el intervalo $[a,b]$ si f es derivable con
derivada continua en dicho intervalo.
Para una curva rectificable definida por $y=f(x)$ para los valores de $x$ comprendidos entre $a$ y $b$ su longitud se puede calcular mediante la fórmula: $$L = \int\limits_a^b {\sqrt {1 + {{\left[ {f'\left( x \right)} \right]}^2}} dx} $$
Para una curva rectificable definida por $y=f(x)$ para los valores de $x$ comprendidos entre $a$ y $b$ su longitud se puede calcular mediante la fórmula: $$L = \int\limits_a^b {\sqrt {1 + {{\left[ {f'\left( x \right)} \right]}^2}} dx} $$
Laboratorio: Aplicaciones de la integral
Cálculos de superficies de revolución
Si consideramos que el sólido se genera girando la función $f(x)$ a lo largo del eje X limitado por las rectas $x=a$ y $x=b$ la superficie de dicho sólido se puede calcular a partir de la fórmula:
$$S = 2\pi \int\limits_a^b {f\left( x \right)\sqrt {1 + {{\left[ {f'\left( x \right)} \right]}^2}} dx} $$Laboratorio: Aplicaciones de la integral
